A Chemist Shines Light on a Surprising Prime Number Pattern

About a year ago, the theoretical chemist Salvatore Torquato met with the number theorist Matthew de Courcy-Ireland to explain that he had done something highly unorthodox with prime numbers, those positive integers that are divisible only by 1 and themselves.

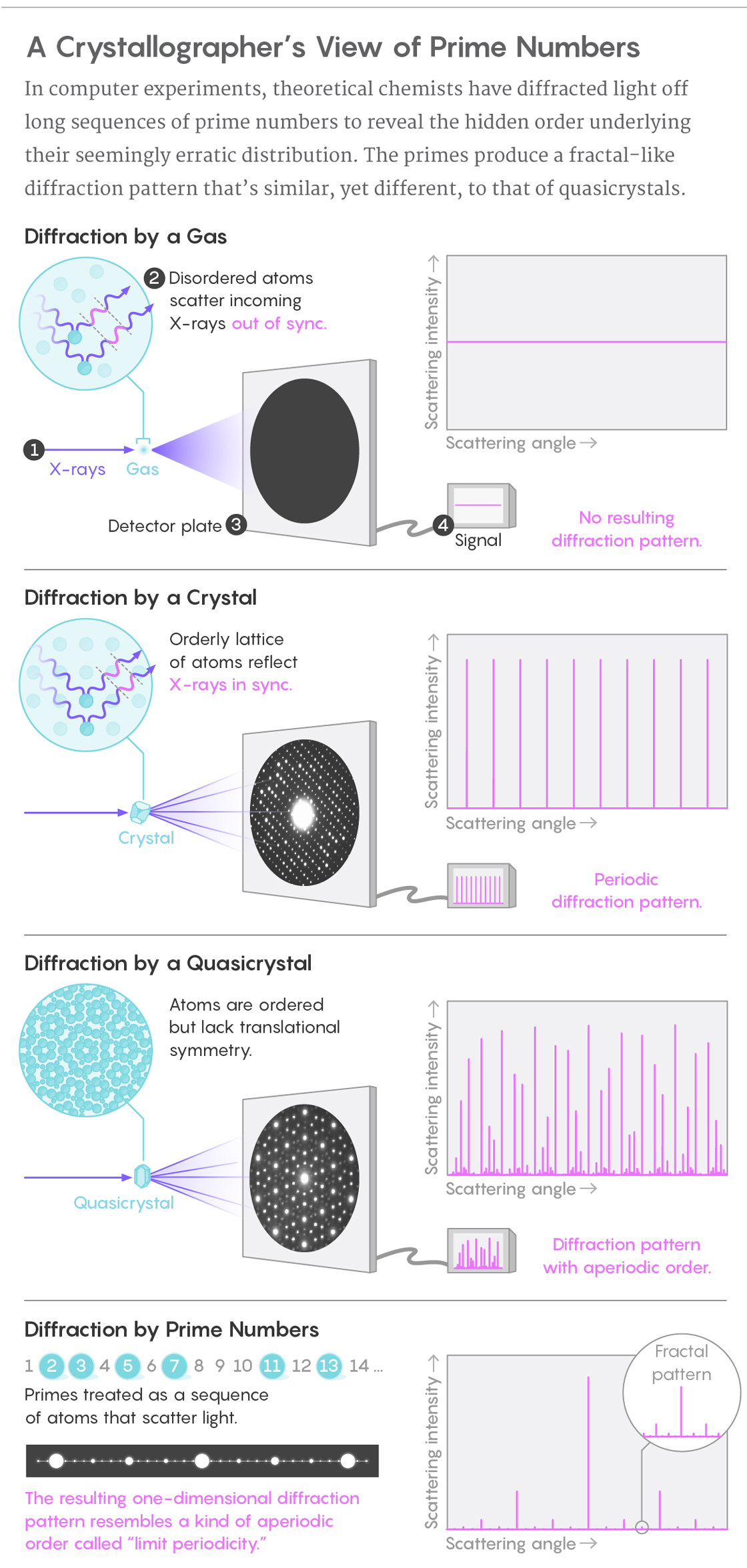
A professor of chemistry at Princeton University, Torquato normally studies patterns in the structure of physical systems, such as the arrangement of particles in crystals, colloids and even, in one of his better-known results, a pack of M&Ms. In his field, a standard way to deduce structure is to diffract X-rays off things. When hit with X-rays, disorderly molecules in liquids or glass scatter them every which way, creating no discernible pattern. But the symmetrically arranged atoms in a crystal reflect light waves in sync, producing periodic bright spots where reflected waves constructively interfere. The spacing of these bright spots, known as “Bragg peaks” after the father-and-son crystallographers who pioneered diffraction in the 1910s, reveals the organization of the scattering objects.

Torquato told de Courcy-Ireland, a final-year graduate student at Princeton who had been recommended by another mathematician, that a year before, on a hunch, he had performed diffraction on sequences of prime numbers. Hoping to highlight the elusive order in the distribution of the primes, he and his student Ge Zhang had modeled them as a one-dimensional sequence of particles — essentially, little spheres that can scatter light. In computer experiments, they bounced light off long prime sequences, such as the million-or-so primes starting from 10,000,000,019. (They found that this “Goldilocks interval” contains enough primes to produce a strong signal without their getting too sparse to reveal an interference pattern.)

It wasn’t clear what kind of pattern would emerge or if there would be one at all. Primes, the indivisible building blocks of all natural numbers, skitter erratically up the number line like the bounces of a skipping rock, stirring up deep questions in their wake. “They are in many ways pretty hard to tell apart from a random sequence of numbers,” de Courcy-Ireland said. Although mathematicians have uncovered many rules over the centuries about the primes’ spacings, “it’s very difficult to find any clear pattern, so we just think of them as ‘something like random.’”

But in three new papers — one by Torquato, Zhang and the computational chemist Fausto Martelli that was published in the Journal of Physics A in February, and two others co-authored with de Courcy-Ireland that have not yet been peer-reviewed — the researchers report that the primes, like crystals and unlike liquids, produce a diffraction pattern.

“What’s beautiful about this is it gives us a crystallographer’s view of what the primes look like,” said Henry Cohn, a mathematician at Microsoft Research New England and the Massachusetts Institute of Technology.

The resulting pattern of Bragg peaks is not quite like anything seen before, implying that the primes, as a physical system, “are a completely new category of structures,” Torquato said. The Princeton researchers have dubbed the fractal-like pattern “effective limit-periodicity.”

It consists of a periodic sequence of bright peaks, which reflect the most common spacings of primes: All of them (except 2) are at odd-integer positions on the number line, multiples of two apart. Those brightest bright peaks are interspersed at regular intervals with less bright peaks, reflecting primes that are separated by multiples of six on the number line. These have dimmer peaks between them corresponding to farther-apart pairs of primes, and so on in an infinitely dense nesting of Bragg peaks.

Dense Bragg peaks have been seen before, in the diffraction patterns of quasicrystals, those strange materials discovered in the 1980s with symmetric but nonrepeating atomic arrangements. In the primes’ case, though, distances between peaks are fractions of one another, unlike quasicrystals’ irrationally spaced Bragg peaks. “The primes are actually suggesting a completely different state of particle positions that are like quasicrystals but are not like quasicrystals,” Torquato said.

According to numerous number theorists interviewed, there’s no reason to expect the Princeton team’s findings to trigger advances in number theory. Most of the relevant mathematics has been seen before in other guises. Indeed, when Torquato showed his plots and formulas to de Courcy-Ireland last spring (at the suggestion of Cohn), the young mathematician quickly saw that the prime diffraction pattern “can be explained in terms of almost universally accepted conjectures in number theory.”

It was the first of many meetings between the two at the Institute for Advanced Study in Princeton, N.J., where Torquato was spending a sabbatical. The chemist told de Courcy-Ireland that he could use his formula to predict the frequency of “twin primes,” which are pairs of primes separated by two, like 17 and 19. The mathematician replied that Torquato could in fact predict all other separations as well. The formula for the Bragg peaks was mathematically equivalent to the Hardy-Littlewood k-tuple conjecture, a powerful statement made by the English mathematicians Godfrey Hardy and John Littlewood in 1923 about which “constellations” of primes can exist. One rule forbids three consecutive odd-numbered primes after {3, 5, 7}, since one in the set will always be divisible by three, as in {7, 9, 11}. This rule illustrates why the second-brightest peaks in the primes’ diffraction pattern come from pairs of primes separated by six, rather than four.

Hardy and Littlewood’s conjecture further specified how often all the allowed prime constellations will occur along the number line. Even the simplest case of Hardy-Littlewood, the “twin primes conjecture,” although it has seen a burst of modern progress, remains unproved. Because prime diffraction essentially reformulates it, experts say it’s highly unlikely to lead to a proof of Hardy-Littlewood, or for that matter the famous Riemann hypothesis, an 1859 formula linking the primes’ distribution to the “critical zeros” of the Riemann zeta function.

The findings resonate, however, in a relatively young research area called “aperiodic order,” essentially the study of nonrepeating patterns, which lies at the intersection of crystallography, dynamical systems, harmonic analysis and discrete geometry, and grew after the discovery of quasicrystals. “Techniques that were originally developed for understanding crystals … became vastly diversified with the discovery of quasicrystals,” said Marjorie Senechal, a mathematical crystallographer at Smith College. “People began to realize they suddenly had to understand much, much more than just the simple straightforward periodic diffraction,” she said, “and this has become a whole field, aperiodic order. Uniting this with number theory is just extremely exciting.”

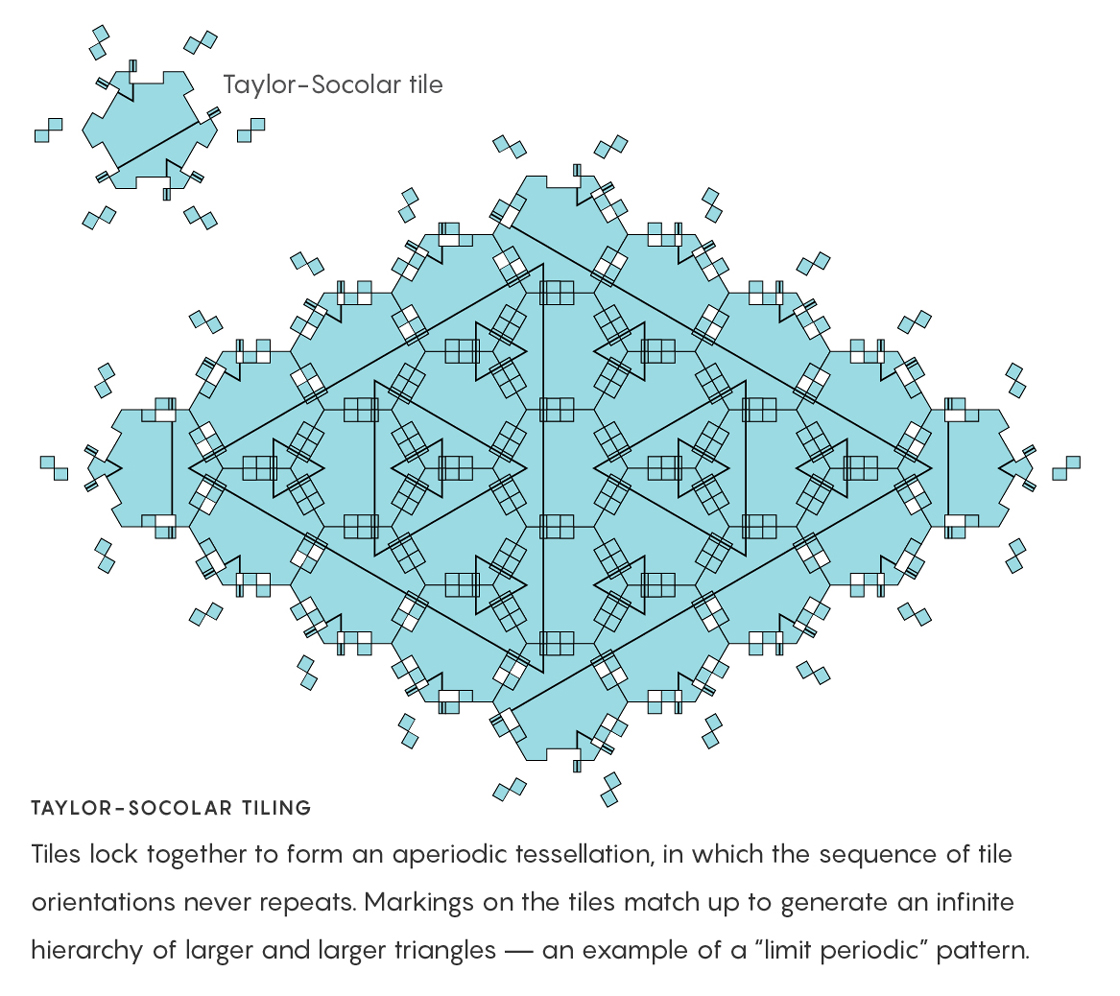
The primes’ pattern resembles a kind of aperiodic order known since at least the 1950s called limit periodicity, “while adding a surprising twist,” Cohn said. In true limit-periodic systems, periodic spacings are nested in an infinite hierarchy, so that within any interval, the system contains parts of patterns that repeat only in a larger interval. An example is the tessellation of a strange, multipronged shape called the Taylor-Socolar tile, discovered by the Australian amateur mathematician Joan Taylor in the 1990s, and analyzed in detail with Joshua Socolar of Duke University in 2010. According to Socolar, computer experiments indicate that limit-periodic phases of matter should be able to form in nature, and calculations suggest such systems might have unusual properties. No one guessed a connection to the primes. They are “effectively” limit periodic — a new kind of order — because the synchronicities in their spacings only hold statistically across the whole system.

For his part, de Courcy-Ireland wants to better understand the “Goldilocks” scale at which effective limit-periodicity emerges in the primes. In 1976, Patrick Gallagher of Columbia University showed that the primes’ spacings look random over short intervals; longer strips are needed for their pattern to emerge. In the new diffraction studies, de Courcy-Ireland and his chemist collaborators analyzed a quantity called an “order metric” that controls the presence of the limit-periodic pattern. “You can identify how long the interval has to be before you start seeing this quantity grow,” he said. He is intrigued that this same interval length also shows up in a different prime number rule called Maier’s theorem. But it’s too soon to tell whether this thread will lead anywhere.

The main advantage of the prime diffraction pattern, said Jonathan Keating of the University of Bristol, is that “it is evocative” and “makes a connection with different ways of thinking.” But the esteemed number theorist Andrew Granville of the University of Montreal called Torquato and company’s work “pretentious” and “just a regurgitation of known ideas.”

Torquato isn’t especially concerned about how his work will be perceived by number theorists. He has found a way to glimpse the pattern of the primes. “I actually think it’s stunning,” he said. “It’s a shock.”