A Primordial Nucleus Behind the Elements of Life

Billions of years ago, all of Earth’s carbon erupted into existence inside distant, dying stars. At first, each atom’s nucleus arose in a swollen, squashed state with little chance of survival. For every 2,500 that immediately fizzled, only one shape-shifted into a stable form capable of supporting life.

That primordial, unstable nuclear state, called the Hoyle state, was discovered more than 50 years ago, but it has taken the rise of modern supercomputers and the development of new mathematical techniques to figure out just how the laws of physics cook it up. In work first detailed in May 2011 and further refined in a paper to be published this month in Physical Review Letters, a group of theoretical physicists in Germany and the United States applied the forces of physics to a computer-simulated set of subatomic particles to build the structure of the Hoyle state nucleus from scratch.

“It looks like a bent arm,” said Dean Lee, a professor of nuclear and particle physics at North Carolina State University and a study co-author.

Physicists say knowing the structure of the Hoyle state will help reveal how it gives rise to carbon, oxygen, nitrogen and other light elements that compose the complex molecules of living things. The synthesis of these elements enables the genesis of life, but it also drives the evolution of stars.

“The carbon-oxygen-nitrogen cycle is simply crucial for the formation of almost all the other elements, and for understanding how stars live and how stars decay and fade away,” said Morten Hjorth-Jensen, a professor of theoretical nuclear physics at the University of Oslo and Michigan State University, who was not involved in the research. “And, of course, without the Hoyle state we wouldn’t be here.”

The quest to unravel the Hoyle state started in 1954 with what the astrophysics writer Marcus Chown has called “the most outrageous prediction” ever made in science. The theoretical astrophysicist Fred Hoyle reasoned that his own existence meant that an unknown, exotic state of the carbon atom with about 7.65 million electron volts of extra energy must arise inside dying stars, even though no one had ever detected spectral emissions from such an atom.

“Hoyle postulated that this 7.65 MeV carbon had to exist in order for there to be life,” Hjorth-Jensen said. “Then, four or five years later, an experimental group in Caltech actually found this Hoyle state in emissions.”

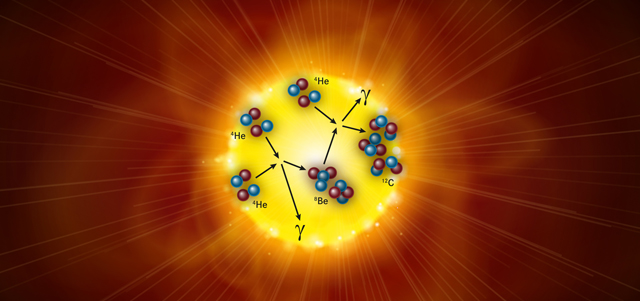
Just as predicted, almost all the key elements of life descend from that fleeting form of carbon. When midsize stars like our sun run low on hydrogen to fuse into helium, their outer layers expand and redden, and their cores shrink. During this inner contraction, helium nuclei (also called alpha particles), each containing two protons and two neutrons, are thrust together so forcefully that they fuse, forming a four-proton, four-neutron atomic nucleus called beryllium-8. In the ten-thousandth of a trillionth of a second before the beryllium decays back into two alpha particles, a third alpha particle sometimes smacks into the beryllium, fusing with it to form an excited, plus-size carbon-12 nucleus: the Hoyle state. In addition to carbon’s usual six protons and six neutrons, this state packs an extra bundle of energy.

Hoyle state nuclei almost always decay right back into beryllium and an alpha particle. But once out of every 2,500 times, these swollen carbons relax into their stable, ground-state configuration, giving off the extra energy as a burst of gamma rays. The brand new carbon-12 nuclei that are created subsequently populate the periodic table: Some stay as they are, while others fuse with another alpha particle to become oxygen. A fraction of the oxygen nuclei are stripped of a proton, transforming into nitrogen; others fuse with yet another alpha to become neon, and so on. If the star ends in a cataclysmic explosion called a supernova, it disperses these newly minted elements into space, where they eventually become the building blocks of future solar systems.

Hoyle, who died in 2001, knew that without the Hoyle state as their starting point, these elements would not arise. The Hoyle state is a “resonance” of carbon formed by a beryllium atom and an alpha particle, meaning it has almost exactly the same energy as their combined masses. Ground-state carbon-12 has a lower energy, and so it does not form through the fusion of an alpha particle and beryllium, just as two plus two does not equal three. “For all these stable states to happen, there must be a resonance,” Hjorth-Jensen said.

But Hoyle only predicted the energy of the resonant state of carbon; he could say nothing about the forces and interactions that enable it to form, nor anything about its physical properties. Because carbon contains six protons and six neutrons, each of which contains three quarks, the Hoyle state amounts to a highly complex 36-body problem. Despite decades of work by nuclear physicists, even with modern computing an exact calculation of the state remains beyond reach.

Now an approach called chiral effective field theory, developed by the Nobel laureate Steven Weinberg, has enabled Lee and his colleagues to closely approximate the structure of the Hoyle state. The trick takes advantage of the fact that protons and neutrons tend to keep their distance from one another inside atomic nuclei, so they “see” one another not as three-quark structures but as single, albeit slightly complicated particles.

Forgetting about quarks turns a 36-body problem into a 12-body problem, but with the strong nuclear force, electromagnetism and “higher-order” chiral forces acting between every particle, even this problem resists an exact solution. “Pinning down where all twelve protons and neutrons are is just a horribly complicated thing,” said Lee.

To make the calculation possible, chiral effective field theory employs a math trick sometimes used in high school calculus. In the same way that a mathematical function, such as a curve on a graph, can be approximated by calculating the first few terms of a “Taylor series expansion” — an infinite sum of progressively smaller terms — around a point on the curve, the researchers approximated the forces that shape the Hoyle state by considering only the first few terms of a Taylor series expansion of those forces.

“I like to compare it to shooting a par-3 in golf,” Lee said. The first stroke, analogous to the leading terms in the Taylor series equation, “drives the ball as close to the hole as possible.” The second stroke, representing the terms with middling influence on the motion of the particles, gets you even closer. The third is a subtle correction. After three strokes, you have a very good approximation of the structure and energy of the Hoyle state.

When a supercomputer applies this calculation to a simulation of six protons and six neutrons distributed on a three-dimensional lattice, the particles can arrange themselves in response to it in infinitely many ways. However, only the lowest-energy configurations of the particles are common in nature. Of these, the researchers found that one of the solutions was the ground-state carbon nucleus. Another was the Hoyle state, with its 7.65 MeV of extra energy.

The calculation, performed by Germany’s JUGENE supercomputer, would have taken a typical laptop more than two centuries to complete.

“When you go from first principles, you are not tuning your model to match the complicated objects you are seeking; you are calculating the objects from the starting point of the most basic interactions between particles,” said Lee, who collaborated with Evgeny Epelbaum, Hermann Krebs, Ulf-G. Meissner and Timo Laehde.

Like a bent arm, the Hoyle state takes the shape of an obtuse triangle with an alpha particle at each vertex. The nucleus’s surplus energy enables its alpha clusters to stretch farther apart from one another than the clusters in ground-state carbon-12, which draw together in a tight equilateral triangle.

Martin Freer, an experimental nuclear physicist at the University of Birmingham, said that knowing the structure of the atomic nucleus will help explain the rates and mechanisms by which it transforms into other states, begetting many of the other elements in the universe. The calculation helps explain why the Hoyle state exists and also promises to reveal just how fine-tuned the universe is for life. “If the Hoyle state were not to exist, neither would we, and even if its energy were slightly different, life would have had to have found an alternate route,” Freer said.

By increasing the resolution of the 3-D lattice in their simulation, Lee and his colleagues hope to refine their picture of the Hoyle state and better understand the physics that makes life possible. “We always want to solve the big questions that intrigue us about ourselves,” Lee said. “When life is at stake, then it becomes interesting.”

This article was reprinted on ScientificAmerican.com.