Alessio Figalli with a crystal-like model at Durham University in England.
Photo by Tom Parker for Quanta Magazine; Illustration by Olena Shmahalo/Quanta Magazine
Introduction
In the company of Alessio Figalli, you get a sense that everything is taken care of. The young Italian mathematician is tall, fit and stylish, his R’s rolling off the tongue with an intoxicating Roman richness. He likes to be around other people, and other people like to be around him. Which is why the secret he has had to keep has been so hard for him.
Over the past few months, he’s visited friends in England, where his wife lives, and in Rome, where he grew up. He’s given lectures before friends and colleagues in Texas, North Carolina, Paris, and the Canadian mountain town of Banff. At each stop he has dined with friends and caught up with longtime collaborators. And under no circumstances has he been allowed to reveal that in February of this year, he received a call informing him that he would be receiving the Fields Medal, the most illustrious honor in mathematics.
“I’m not telling this to anyone, which means as a result you don’t really realize it,” said Figalli, a professor at the Swiss Federal Institute of Technology Zurich, back in April. “It’s a weird feeling, I’ve never experienced it. You don’t have feedback, not even from your friends.”
Now Figalli’s wait is over. This morning, at the 28th meeting of the International Congress of Mathematicians in Rio de Janeiro, he was officially named one of the four winners of the Fields Medal. The prize is conferred every four years by the International Mathematical Union to the most accomplished mathematicians in the world under the age of 40. At age 34, Figalli won the award with time to spare.
For Figalli, the Fields Medal caps a string of honors he has received during his ascent to the top of the math world. Once a classics student with no particular affinity for mathematics, he has gone on to shake the venerable mathematical discipline of analysis, which concerns the properties of certain types of equations. Figalli’s results have provided a refined mathematical understanding of everything from the shape of crystals to weather patterns, to the way ice melts in water.
“He has a wild spectrum of different contributions,” said Luis Caffarelli, a mathematician at the University of Texas, Austin, who will introduce Figalli at the Fields Medal ceremony in Rio.
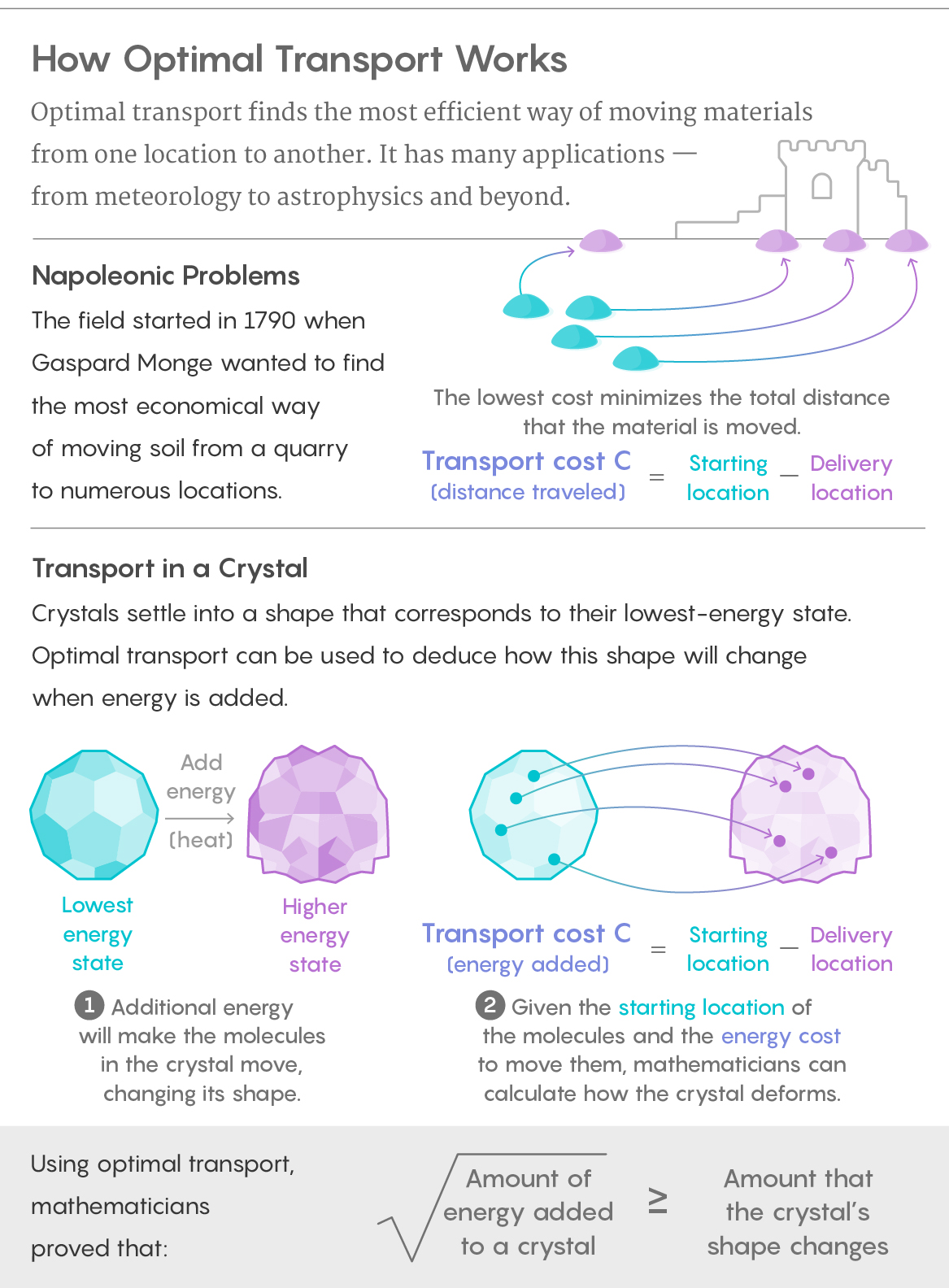
While Figalli’s mathematical results are diverse, many of them turn on the innovative use of a concept called optimal transport. The idea originated in the 18th century, when a mathematician working for Napoleon Bonaparte tried to find the most efficient way to build a network of earthen fortifications. More than two centuries later, Figalli leads a community of mathematicians who have recognized that disparate mathematical problems will yield if you view them as the best way of moving a pile of dirt from one place to another.
Quick Study
Figalli was born in Rome in 1984. His father was a professor of engineering and his mother was a high school classics teacher. The Figalli home was full of books on Greek history and mythology. As a kid Figalli liked to play soccer, watch cartoons, and hang out with his friends — and, he recalls, he always made the rational decision to get his homework done first, so that he could fully enjoy himself.
“For me it was always a balance between how good a grade I could get and how much time I had to spend to get such a grade,” he said. “I was always an optimizer, I wanted the best for the least effort.”
Figalli liked math from an early age. He regarded it as an easy subject, something he was good at without having to work hard, and it took him a while to pursue the subject with any zeal. In Italy, students can enroll in either a classics or a scientific high school. Figalli had a taste for science, but his parents wanted him to study the classics, and he went along with this willingly.
“I said: ‘Why not?’ Usually there are more girls in a classics high school than a scientific high school, so that was another selling point,” he said.
Figalli turned toward serious math in his third year of high school. A mathematician colleague of his father’s encouraged Figalli to participate in the International Mathematical Olympiad, an open-ended problem-solving contest that draws the best young math minds in the world. Figalli was fascinated to discover that there were math problems whose solutions were not straightforward — you had to invent them yourself. “I loved that. It was a revelation,” he said.
Emboldened, Figalli tested into the Scuola Normale Superiore of Pisa, a university for mathematically and scientifically gifted students. There Figalli quickly confronted the limits of his education: At 18 he was sitting in math classes with the top students in Italy and he didn’t even know how to take a derivative.
“He didn’t [stand out] because he had a gap to recover compared to these highly trained colleagues,” said Luigi Ambrosio, a mathematician at the Scuola Normale and Figalli’s graduate school adviser.
But to anyone who looked closely, Figalli’s promise was apparent. He learned quickly and caught up to his peers within a year. At the start of his second year he began to work on a highly technical paper that Ambrosio had recently written. Ambrosio expected that the novice student would struggle to get anywhere with it. “Alessio came to me less than one week after and I realized he understood everything,” Ambrosio said. Figalli completed his undergraduate degree in two years.
In 2004 Ambrosio took him on as a graduate student and also arranged for him to study under Cédric Villani, a talented mathematician in Lyon, France, who would go on to win the Fields Medal himself a few years later. At the time Villani was working on a book about an intuitive idea that was experiencing a mathematical renaissance — an idea whose origins stretched back to the French Revolution.
Dirty Math
In the 1790s Gaspard Monge had a problem. He was a mathematician tasked by Napoleon with figuring out how to transport soil to the front for building fortifications. Monge wanted to find the optimal way to complete this transport — that is, he wanted to know which wagonload of dirt should end up where, so as to minimize the labor required to complete the task.
Monge made some headway on the problem, but then it languished for more than a century. It resurfaced in the 1940s when the economist Leonid Kantorovich produced the first rigorous mathematical description of optimal transport. But for decades afterward it remained of interest mainly to economists. It wasn’t until the 1980s and 1990s that mathematicians began to recognize that optimal transport was a mathematically deep question in its own right and also a tool that they might use to solve other kinds of problems.
Optimal transport is so intuitive that it’s easy to overlook the mathematical complexity it contains. The complexity comes from the enormous range of possibilities for how to move a pile of material from one place to another (or how to move many piles from many starting locations to many different destinations).
For instance, you’re not limited to transporting soil by the wagonload. Maybe it makes sense to split one wagonload between two destinations. Or to divide your pile into wheelbarrow loads, or to break it down by the shovelful, sending each one to a unique, carefully chosen destination. You can make your unit of transport infinitely small in your quest to find the optimal way to move material around — and this is where analysis comes in, as an extended form of calculus, the study of change on infinitely small or large scales.
Lucy Reading-Ikkanda/Quanta Magazine
“You can decide this piece goes here, that piece goes there. You have infinite degrees of freedom, and it’s only with advanced mathematical tools that you can really get rid of this infinite dimensionality and find in some sense your solution,” Ambrosio said.
By the time Figalli began to study at the Scuola Normale, mathematicians had recognized that the mathematics behind optimal transport was useful for much more than moving dirt. They realized that whenever you want to compare two shapes — which is something mathematicians often want to do — you can learn something by thinking about the most efficient, or optimal, way of converting one into the other.
Essential Traits
Figalli has been on the faculty at ETH Zurich since 2016, when he moved from UT Austin. In Zurich he lives in a furnished apartment on a hillside above the campus. He is rarely there for more than two weeks at a time. Instead, he’s often in England, where his wife, Mikaela Iacobelli, is a mathematician at Durham University. They met in 2013 when Figalli gave a talk at the University of Rome, where Iacobelli was a doctoral student. Iacobelli recalls being struck by the way Figalli reacted when the faculty member introducing him recited a long list of his accomplishments.
“Alessio looked a bit embarrassed, and I found this very nice because he’s really humble. I always forget about how good he is at math in our normal life,” she said.
Figalli has many collaborators around the world. He maintains a frenetic travel schedule — he claims he’s relatively unaffected by jetlag — and also frequently hosts other mathematicians in Zurich. This past May, David Jerison of the Massachusetts Institute of Technology visited Figalli with the hopes of making headway on a problem related to the Brunn-Minkowski inequality. They began to work through their various ideas at a blackboard. At times they grew quick and excited as they played out the consequences of some promising new suggestion. At other moments they’d be silent for a minute or more after they realized that the idea didn’t work, Jerison seated with his head in his hands, Figalli leaning against the wall, trying to figure out where to go next. But by just the second day, they had made some real progress. “Alessio is unbelievably quick,” Jerison later said. “Quick on the essential issues, and quick on isolating an important point that is going somehow to yield information for us.”
Figalli’s quickness is something many of his colleagues remark on — both the quickness with which he works through technical details and the speed with which he understands the crux of a new problem. Francesco Maggi, a mathematician at UT Austin, remembers that when he started working with Figalli on crystal stability, in next to no time Figalli knew as much about the subject as Maggi himself.
“One thing that was amazing about working with Alessio when he was a student was seeing how quick he was once he had a new idea,” Maggi said. “He had this rare ability of immediately placing the idea in the right context and using it creatively.”
When facing any new problem, Figalli likes to begin by developing a geometric sense of how the problem behaves. With crystals, for instance, he sketched some of the most extreme ways a crystal could deform under heating, knowing that an eventual stability proof would have to account for those cases.
“I like drawing pictures. I get an intuition of what’s going on and I can easily catch what are the key issues,” he said.
It takes a lot of different traits to be a successful mathematician — technical skill, ingenuity, an ability to persevere under great uncertainty. Figalli has a generous helping of each of these, but what stands out most about him is his disposition: He doesn’t seem weighed down by mathematics.
“Alessio does not show any pain,” Ambrosio said. “Maybe there is some pain, but it’s not apparent. He has a very plain, friendly personality, which I think is a good ingredient of his success.”

Figalli in the math department of Durham University.
Tom Parker for Quanta Magazine
Unexpected Inspiration
In Italian mathematics there is a long history of studying what are called “minimal surfaces,” which are shapes that minimize some quantity. The circle is a simple example of a minimal surface in that it’s the shape that minimizes the perimeter required to enclose some amount of area.
Minimal surfaces appear in many areas of mathematics. They’re also familiar in everyday life. Think about blowing a soap bubble, for example: The bubble elongates and wavers as it expands from the wand, but after it detaches it settles into the shape of a sphere. The reason is that for soap film, the sphere is the most stable shape — it’s the shape that takes up the least amount of surface area and thus requires the least energy to maintain. Crystals are another minimal shape. They look the way they do — symmetric and polygonal — because for crystalline materials, that is the shape that uses the least amount of energy.
Figalli’s first major result as a mathematician had to do with proving the stability of these types of energy-minimizing shapes. Stability proofs such as these are a specific and important variety of mathematical result. They are a way of validating the mathematical representations of physical phenomena. When physicists say a soap bubble is stable, they mean that if you nudge it slightly, it only wavers slightly — the nudge doesn’t induce a dramatic change in shape. Mathematicians have developed formulas and inequalities that are meant to describe what happens when you nudge a soap bubble; they’d like to prove that those mathematical representations feature a degree of stability that matches what we observe in nature.
Similarly, with crystals, you might ask: If I start with a perfect crystal, then add a small amount of energy by heating it a bit, is the resulting shape similar to the one I started with or dramatically different? Empirically it’s obvious that the two shapes don’t differ much. But mathematicians would like to precisely quantify that stability.
In work completed in 2007 and published in 2010, Figalli, Maggi and Aldo Pratelli gave a quantitative proof of the stability of energy-minimizing shapes like crystals and soap bubbles. (Though soap bubbles and crystals look very different, the mathematics involved with analyzing their stability is the same.) Figalli remembers the moment they found the key idea they needed to create a proof. He and his collaborators were at a conference in Edinburgh, where they had been working on the stability problem for many hours a day. They were walking home from a bar at around one in the morning when Maggi realized that maybe they could use a theorem called the trace inequality to overcome the last barriers to a proof.
“Francesco said something like, ‘We could have used the trace inequality, but I’m not sure it works,’ and I was like, ‘Wait, that’s it!’ The moment he said that word it was so neat in my mind,” Figalli said.
Their proof takes the form of a precise inequality, which says that if you increase the energy of a system like a soap bubble or a crystal by some amount, then the resulting shape will deviate from the original shape by no more than some other amount. They also proved that their inequality is the optimal one, meaning it places a strict limit on the extent to which the additional energy will distort the shape of the crystal.
“We proved if the size of the added energy is some given amount, then the distance from the perfect shape will be at most this other amount. It’s quantitative in a sharp way,” Maggi said.
This inequality relates back to optimal transport. Imagine that you start with a perfect crystal and then deform it slightly through heating. Now imagine that the two versions of the crystal are positioned next to each other. What you really want to know is whether the two are in a stable relationship with each other. One way to investigate that question is to consider the optimal way of moving all the material from the original crystal into the slightly larger deformed crystal. If you can prove something about the optimal transport map between the two shapes, you prove something about the relationships between the shapes themselves.
“The point is, all the properties of the new objects that you want to understand are encoded in the transport,” Figalli said. “You translate the question from understanding the shape of an object to understanding the transport map.”
Figalli’s second major result had a similar flavor. In 2011 and 2012 he published successive papers with Guido De Philippis, now at the International School for Advanced Studies in Trieste, Italy. The first proved the “regularity” of the Monge-Ampère equation, which is found throughout geometry. (It’s named after the very same Monge who was trying to help Napoleon build fortifications.) Like stability, regularity is one of the most important things to know about any mathematical representation of a physical phenomenon. In physical terms, regularity means that a system evolves in a smooth way. If you spot a cloud in the sky and watch how it changes shape, you’ll see that it changes gradually. It doesn’t rupture into a dramatically new shape. If you were to describe the evolution of the cloud mathematically, you’d like to see the same thing: As you gradually change the inputs to an equation, the output of the equation (which represents the shape of the cloud) changes only gradually as well.
The general result about the Monge-Ampère equation allowed them to then prove the regularity of the semigeostrophic equations, which are used in meteorology to model the movement of weather fronts. Here, again, their work incorporated optimal transport. Figalli and De Philippis thought about the optimal transport map that converts the initial shape and position of a front into its subsequent shape and position. They proved that points that are close together in the initial shape remain close together in the subsequent shape — and then they showed how this feature of the transport map implies the regularity of solutions to the semigeostrophic equations.
“This was something that was originally proposed by people in meteorology, and then in some sense Alessio managed to do deep pure mathematics,” Caffarelli said. “He has this combination of taking a problem that is in principle a natural problem from some other area, and he does his mathematics, and provides a solution.”




