Bongard Problems and Scientific Discovery

Olena Shmahalo/Quanta Magazine
Introduction
Unlike most puzzles that are solved by applying rules, Bongard problems go to the heart of scientific discovery: They give you two sets of six related figures, the left-hand set consisting of examples that satisfy some unknown rule, and the right-hand set having items that break the rule. Your task, like that of a scientist faced with messy data from nature, is to figure out the rule.
Can you solve these three Bongard problems and discover the hidden laws in this toy universe?
Problem 1
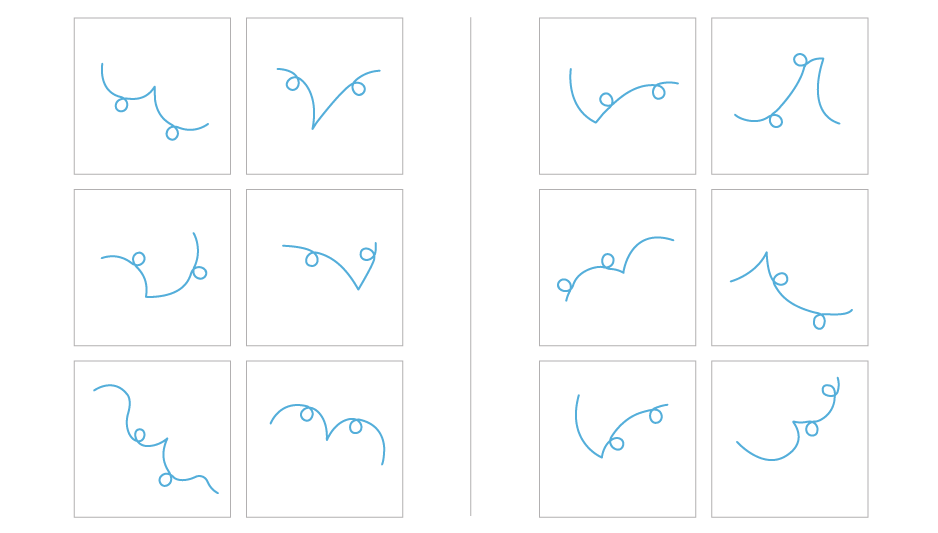
Courtesy of Harry Foundalis. Bongard Problem 44 (Designer: M.M. Bongard)
Problem 2
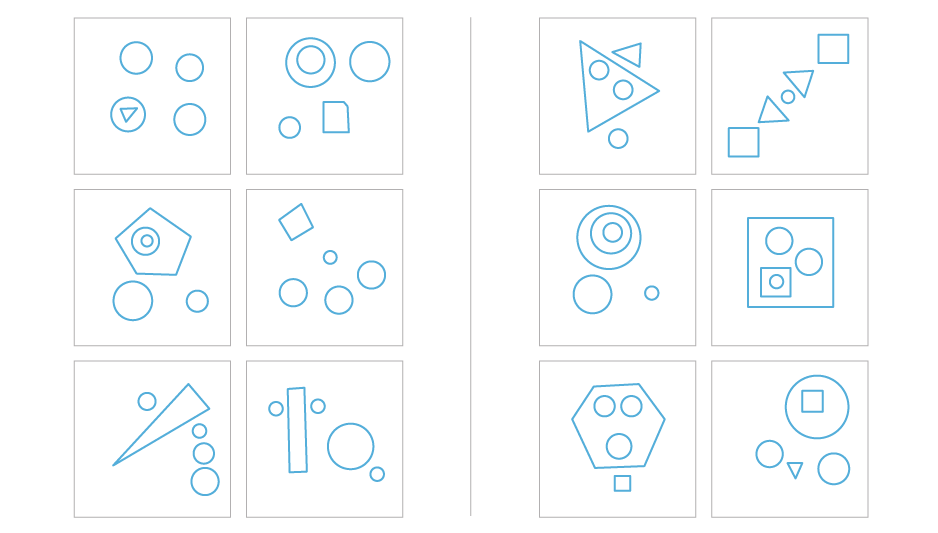
Courtesy of Harry Foundalis. Bongard Problem 110 (Designer: Douglas Hofstadter)
Problem 3
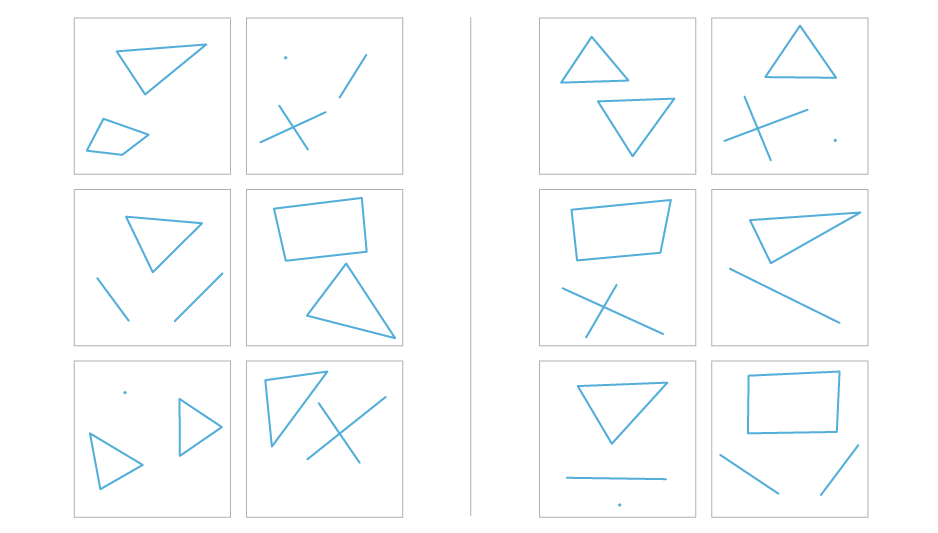
Courtesy of Harry Foundalis. Bongard Problem 230 (Designer: Joseph A.L. Insana)
These kinds of problems — named after their inventor, the Russian computer scientist Mikhail Bongard — have fascinated me ever since I came across Douglas Hofstadter’s deep and discursive meditation into human and computer intelligence, the Pulitzer Prize-winning 1979 book Gödel, Escher, Bach: An Eternal Golden Braid. Harry Foundalis, Hofstadter’s doctoral student, built an automated system to solve such problems and has a website that lists close to 300 of them. The visual nature of these problems reveals a great deal about human perception and cognition, which Foundalis describes nicely on his site. The primitive spatial functions required to reason about these problems, such as the ability to detect shapes in different sizes and orientations, are relatively hard to program into computer algorithms, but our visual system, honed by evolution, accomplishes them automatically.
Like the process of scientific discovery, Bongard problems and code-breaking games like Mastermind require the use of inductive reasoning. This generally means going from the particular to the general (as enshrined in the mnemonic PIG, for particular-inductive-general). In contrast, most mathematical problem solving relies on deductive methods, in which you reason from a known general rule to a particular conclusion. Whereas the conclusions from deductive reasoning follow entirely from the initial assumptions, inductive rules, and therefore scientific conclusions, are basically well-supported guesses that fit existing data well. The problem is that many possible rules can fit the data, as we discussed in a previous inductive puzzle, “Be Still My Pulsating Sequence.”
In science, this problem is addressed in two ways: you can collect more data to distinguish among alternative theories, or you can appeal to aesthetic criteria, such as the simplicity and elegance of the rules. Often these aesthetic considerations give the right answer, as Einstein found with general relativity, but sometimes they can lead you astray, as he found with unified field theory. While nature’s solutions are usually beautiful, nature has no problems being ugly when it needs to be. Fermat’s last theorem, for instance, did not turn out to have a simple, elegant proof, nor did the four-color theorem.
In Bongard problems, of course, you do not have additional data, so simple, elegant rules are definitely preferred. As in science, this means that you should come up with rules that are not complex and disjunctive (that is, they do not have multiple “or” statements); do not have special cases or exceptions; and do not make use of arbitrary parameters. Each example should independently satisfy the rule, and its position in the set should be irrelevant.
As with the process of scientific discovery, Bongard problems initially arouse puzzlement and even frustration as your mind struggles to find the key features behind a working rule and to ignore distracting features of no importance. If you are successful, the negative emotions will be replaced by the glorious “aha!” moment of joy and certainty. I invite readers to share tales of such emotional experiences in the pursuit of real scientific problems. Such aha! moments are cited by many scientists as their motivations to do science in the first place.
Here, for your further frustration and joy, are two more Bongard-type problems, this time with lists of numbers that do or do not follow their hidden rule.
Problem 4
Follow the rule: 65 12 47 38 96 29
Don’t follow the rule: 53 26 93 19 68 37
Hint: Carry out an arithmetical operation on the two digits.
Problem 5
Follow the rule: 50 58 21 74 91 78
Don’t follow the rule: 11 26 35 57 48 88
Hint: Express the numbers in non-Arabic notation.
Finally, here’s a problem that uses words from our favorite science magazine:
Problem 6
Follow the rule: QUANTA PUZZLE PHYSICS MOLECULAR BIOLOGY VIDEO
Don’t follow the rule: SCIENCE MAGAZINE INSIGHTS PROBLEMS ARTICLES COMPUTER
Hint: The key lies in the shapes of the letters.
I’ve provided hints (click on the “Hint” links above) in case these prove too frustrating. I encourage readers to come up with their own Bongard-style problems and post them here. It’s fun. Happy puzzling!
Editor’s note: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt. And if you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION.” (It will not appear online, so solutions to the puzzle above should be submitted separately.)
Note that we may hold comments for the first day or two to allow for independent contributions by readers.
Update: The solution has been published here.



