Computer Scientists Attempt to Corner the Collatz Conjecture

Marijn Heule, a computer scientist at Carnegie Mellon University, is skilled at turning intractable math problems into solvable computer problems. But can he work his magic on the infamous Collatz conjecture?
Introduction
In the last few years, Marijn Heule has used a computerized proof technique called SAT solving (where SAT stands for “satisfiability”) to conquer an impressive list of math problems: The Pythagorean triples problem in 2016, Schur number 5 in 2017 and now Keller’s conjecture in dimension seven — a result that Quanta covered in our recent article, “Computer Search Settles 90-Year-Old Math Problem.”
But Heule, a computer scientist at Carnegie Mellon University, has set his sights on an even more ambitious target: the Collatz conjecture, considered by many to be the most notorious open problem in mathematics (if also one of the simplest to state). When I mentioned to other mathematicians that Heule was attempting this, their first response was incredulity.
“I don’t see how you’d ever completely solve it using SAT solving,” said Thomas Hales of the University of Pittsburgh, a leader in the field of computer proofs. The technique effectively helps mathematicians solve problems — some with infinite possibilities — by turning them into discrete, finite problems.
Yet Hales, like others, was wary of underestimating Heule. “He’s very good at finding clever ways of encoding problems as SAT problems. He’s just outstanding at doing that.”
Scott Aaronson of the University of Texas, Austin, who is collaborating with Heule on the Collatz work, added, “Marijn is someone who has a hammer, which is SAT solving, and he may be the world’s greatest wielder of that hammer right now. He tries it on pretty much everything.” Time will tell if he can transform Collatz into a nail. (June 11, 2021 Update: The paper is now available here.)
SAT solving involves taking problems, turning them into computer-friendly statements that use propositional logic, and using computers to determine whether there’s a way to make those statements true. Here’s a simple example.
Let’s say you’re a parent trying to arrange childcare. One babysitter can work all week except Tuesday and Thursday. Another can work all week except Tuesday and Friday. A third can work all week except Thursday and Friday. You need to cover Tuesday, Thursday and Friday. Can you do it?
One way to find out is to turn the babysitting constraints into a formula that you feed into a SAT solver. The program will figure out whether there’s a way of assigning days to the babysitters that makes the formula true, or “satisfiable,” meaning you get the three days you want. In this case you’re in luck — there is.
Unfortunately, many of the most important questions in math don’t immediately resemble SAT problems. But sometimes they can be rephrased as satisfiability questions in surprising ways.
“It’s hard to predict when a problem will be reduced to a huge but finite computation,” Aaronson said.
The Collatz conjecture is one of those math questions that, at first, look nothing like the babysitting problem. It says to pick a number, any number you want (provided it’s a nonzero whole number). If it’s odd, multiply it by 3 and add 1; if it’s even, divide by 2. Now you have a new number. Apply the same rules, get a new number and keep going. The conjecture predicts that no matter what number you started with, eventually you’ll end up at 1, at which point you’re stuck in a little loop: 1, 4, 2, 1.
Despite nearly a century of effort, mathematicians haven’t come close to proving it.
But that didn’t stop Heule from trying. In 2018, he and Aaronson — colleagues at Austin at the time — received funding from the National Science Foundation to apply SAT solving to the Collatz conjecture.
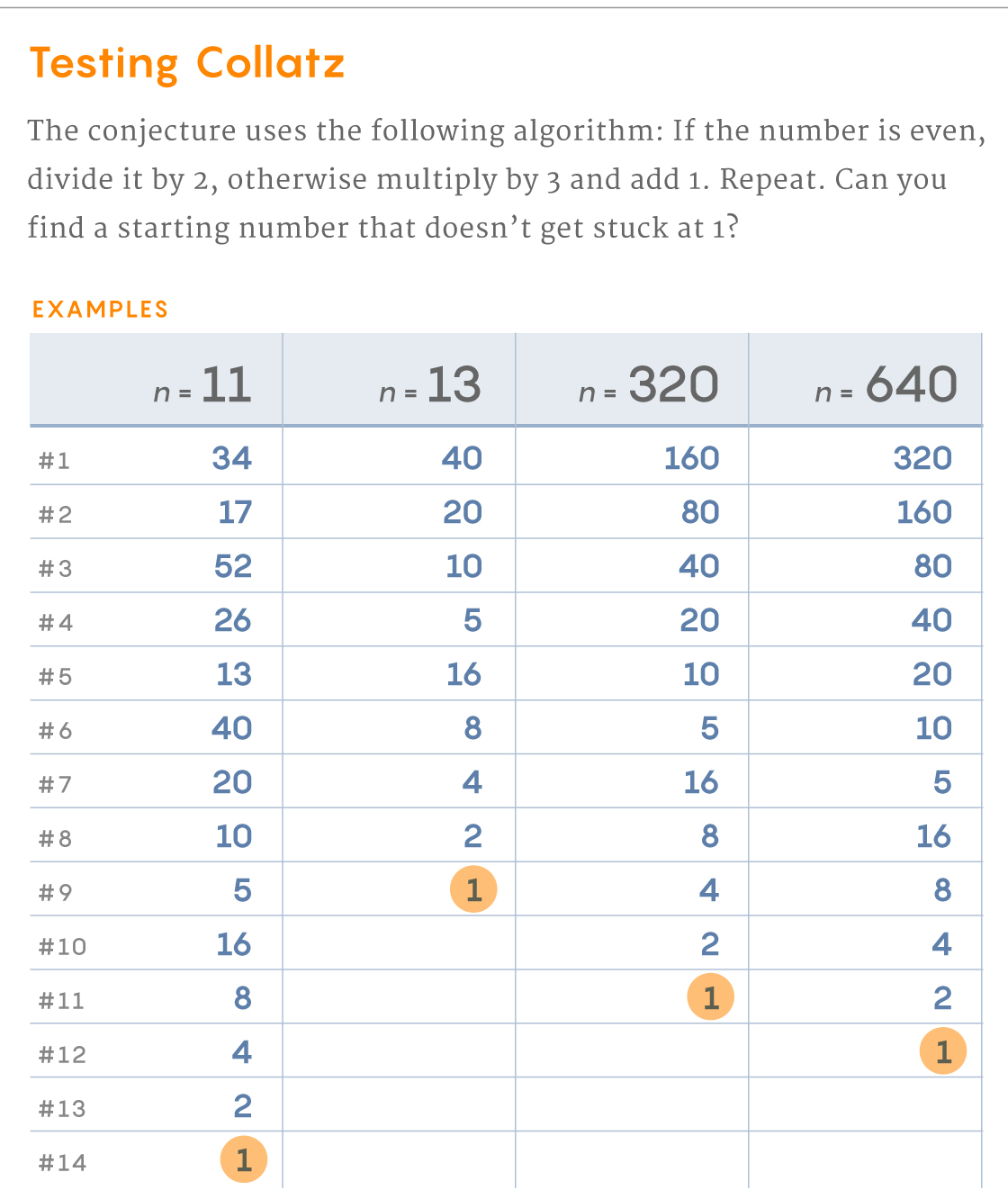
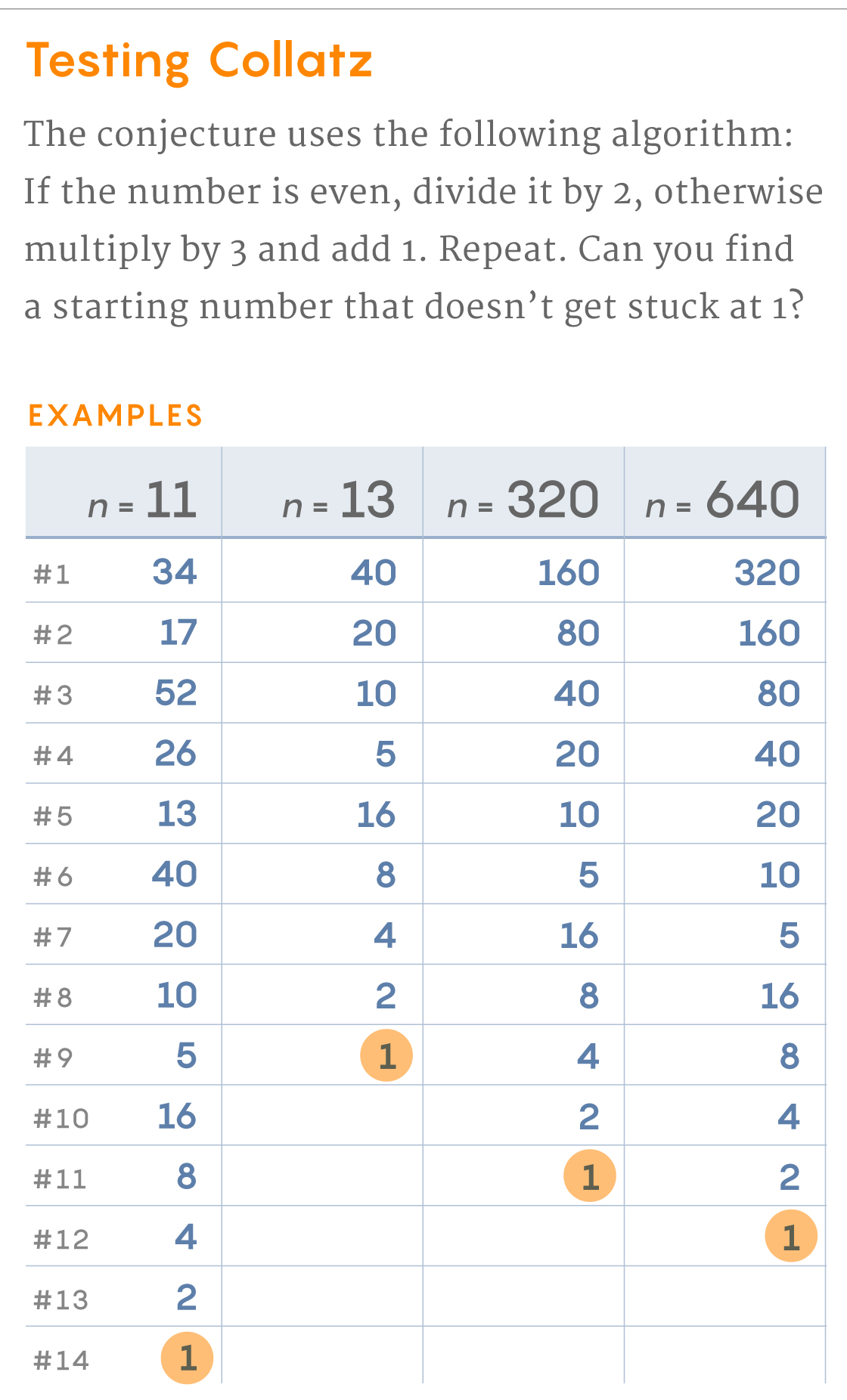
Try it for yourself here.
Lucy Reading-Ikkanda/Samuel Velasco/Quanta Magazine
As a first step, Aaronson, a computer scientist, came up with an alternate formulation of the Collatz conjecture, called a rewriting system, that was more natural for computers to work with.
In a rewriting system, you have a set of symbols, like the letters A, B and C. You use them to form sequences: ACACBACB. You also have rules for transforming those sequences. One rule might say that wherever you see “AC” you replace it with “BC.” Another might replace “BC” with “AAA.” You can have any number of rules specifying any kinds of transformations you want.
Computer scientists are generally interested in knowing whether a given rewriting system always terminates. That is, regardless of the string you start with and the order in which you apply the rules, does the string eventually transform into a state where there are no more rules you can apply to it?
Aaronson came up with a rewriting system with seven symbols and 11 rules that was analogous to the Collatz procedure. If he and Heule could prove that this rewriting system always terminates, they’d prove that the conjecture is true.
To turn Collatz into a SAT problem, Aaronson and Heule had to take one more step. It involved matrices, which are arrays of numbers. They needed to assign a unique matrix to each of the symbols in their rewriting system. This approach — a common way of trying to prove that rewriting systems terminate — would allow them to think of transformations of symbols as matrix multiplication. The seven matrices representing the seven symbols in the rewrite system needed to satisfy a number of constraints, reflecting the ways that the 11 rules needed to be consistent with each other.
“You try to find matrices that satisfy these constraints,” said Emre Yolcu, a graduate student at Carnegie Mellon who is working with Heule on the problem. “If you can find them, you prove [they’re] terminating,” and by implication, you prove Collatz.
The question “Do there exist matrices that meet these constraints?” is a SAT-solver kind of problem. Aaronson and Heule started the SAT solver on small 2-by-2 matrices. It didn’t find any that worked. Next they tried 3-by-3 matrices. Again, no luck. Heule and Aaronson kept increasing the size of the matrices, hoping they’d find the right ones.
However, this approach could only go so far, because the complexity of searching for the right matrices grows exponentially as the matrices get bigger. Heule estimates anything larger than 12-by-12 matrices overwhelms present-day computing power.
“As soon as the matrices become too complex, you can’t solve the problem,” he said.
Heule is still working on optimizing the search, trying to make it more efficient so that the SAT solver can check larger and larger matrices. He and his collaborators are working on a paper summarizing what they’ve discovered so far, but they’re nearly out of ideas and will likely have to give up on Collatz soon — for now, at least.
After all, the tantalizing appeal of SAT solving is that if you can just figure out how to check one more case, call one more babysitter, prolong the search just a little longer, you might find what you’re looking for. In that respect, Heule’s top asset might not be his skill with a SAT solver. It might be his love of the chase.
“I’m just an optimistic guy,” he said. “I feel frequently lucky, so I just give it a try and see how far I get.”



