Color-Changing Material Unites the Math and Physics of Knots

Mathematicians have created new simulations of knots based on experimental data.
Introduction
One sunny day last summer, Mathias Kolle, a professor at the Massachusetts Institute of Technology, took a couple of eminent colleagues out sailing. They talked about their research. They had some drinks. Then Kolle noticed something was off: A rowboat tied to his boat had come loose and was drifting toward the horizon. As he tacked across the water to retrieve the wayward vessel, he realized his mistake. In securing the rowboat, he must have tied the knot wrong.
“I almost lost a boat because I got one knot wrong,” said Kolle, a mechanical engineer. “That was pretty embarrassing.”
This slip-up aside, Kolle has become quite the knot wonk. In a recent paper in Science, he and his colleagues used a new way of visualizing the forces inside tangled fibers to revisit an ancient question: What makes some knots stronger than others?
Scientists have a long-standing fascination with knots. More than 150 years ago, Lord Kelvin — working with fellow Scottish scholar Peter Guthrie Tait — proposed that the chemical elements could be represented by different knots. The theory didn’t pan out, but the diagrams they drew of different knots, and their attempts to classify them, jump-started the development of modern knot theory.
In the 20th century, researchers built on this legacy by developing mathematical descriptions of knots that distinguish one from another. Often these descriptions employ topological properties: simple, countable characteristics that don’t depend on size or shape, such as how often strings in a knot cross.
The mathematics of theoretical knots tied in theoretical strings inspired biologists to investigate how real DNA and proteins twist and tangle. Scientists have also developed theoretical models for knots at larger scales, like the hitches that bind ropes to poles. Some have put their models to the test, using titanium wire to determine how much force is needed to pull a knot tight, or using fishing line or strands of spaghetti to explore what parts of a knot tend to break.
“It’s a creative art in my mind, being able to develop an experiment that will capture these properties,” said Ken Millett, a knot theory pioneer at the University of California, Santa Barbara.
But these experiments all tend to have the same limitation — one that makes it difficult for researchers to truly understand how everyday knots operate, said Jörn Dunkel, a mathematician at MIT.
“The problem is that you could not look inside the material,” Dunkel said. “A lot of things are hidden on the inside.”

Researchers simulated which parts of a knot felt the most stress (top row), then compared the results to actual knots made from special fibers that changed color based on strain.
Joseph Sandt (experiment); Vishal Patil (simulations)
Kolle and his wandering rowboat would agree. But a few years ago, he received inspiration from an unexpected source: a vivid blue seed mailed to a colleague, in a matchbox, by a reporter in Mexico. Plucked from the colorfully named bastard hogberry, the fruit gets its hue from the arrangement of cells in light-bending patterns.
Kolle adapted this optical trick to create plastic fibers that not only shine brightly in white light, but change color when stretched or bent. As their microscopic structures deform, the fibers turn yellow, green and other shades, revealing the stresses and strains within.
Dunkel realized the stretchy fibers could reveal what was hidden within knots, so he and the study’s co-authors set to work constructing new simulations. They modeled not only simple knots in a single rope — the typical subjects of knot theory — but also bends, a rarely studied knot that holds two separate ropes together. Once they estimated the stresses inside several bends and calculated how much force would undo them, the team set about testing their simulations, comparing them to the hues that emerged in knotted-up fibers.
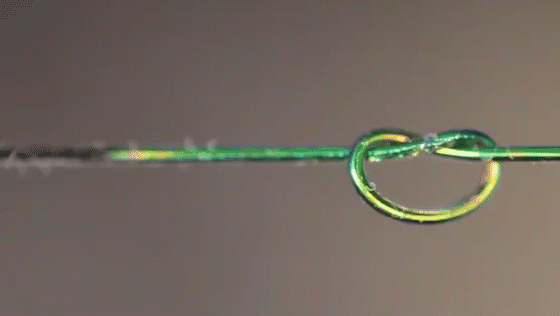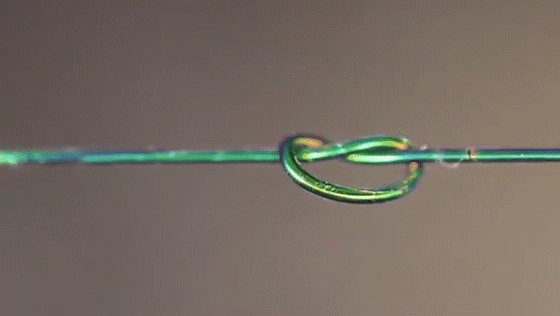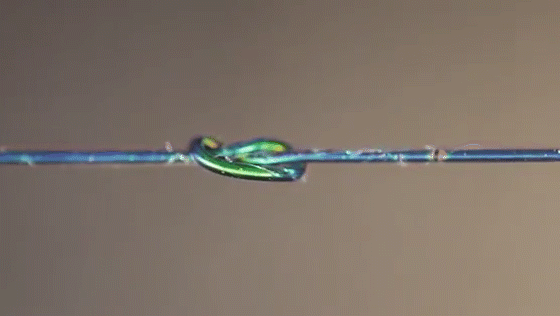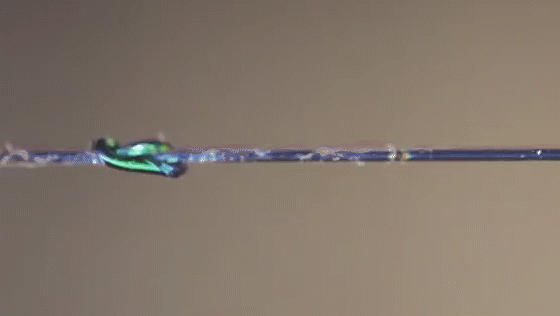
A new material changes colors based on the tension it’s feeling, allowing scientists to visualize the forces within different knots.
Joseph Sandt
After some fine-tuning, the models held up as strongly as the knots they depicted, accurately gauging the relative strengths of different bends.
“My favorite knot was the Zeppelin, which had a nice symmetry and was one of the best we found,” said Vishal Patil, a co-author and an MIT graduate student. The Zeppelin knot, formed from two loops laid on top of each other, gets its strength from countable topological properties, said Patil: lots of rope crossings that tend to twist each other in opposite directions, like a towel being wrung out, and circulate in opposite directions to create friction.
So far, the research has mathematically confirmed the strengths of time-tested knots developed over eons of human experimentation. But Dunkel’s team hopes the findings will play a role in designing new ways to tie, loop, twist and otherwise form tangles from rope, adding a new predictive dimension to knot theory.
“The paper is a very interesting blend of experimental work and qualitative theoretical work,” said Louis Kauffman, a topologist working in knot theory at the University of Illinois, Chicago. He cautioned, however, that the more complicated the knot, the less accurate the predictions become. “The results are best for small tangles,” he said. The work also doesn’t compare different materials, focusing only on a knot’s topology, so the new models can’t predict how a knot tied in a coarse rope will fare against the same knot tied in a smooth ponytail, Rapunzel-style.
Still, the work contributes much-needed real-world data to knot theory, and Millett has been circulating the paper to other mathematicians in the field. “The fact that they have this material that they can use to identify the stresses in the configuration: That’s a new wrinkle,” he said.
This article was reprinted on Wired.com and in Spanish at Investigacionyciencia.es.



