Cryptographers Achieve Perfect Secrecy With Imperfect Devices

Maylee for Quanta Magazine
Introduction
In Ian Fleming’s first novel, James Bond returns from the Royale-les-Eaux casino to his hotel room and inspects it for signs of intrusion. First, he confirms that a hair carefully placed inside his writing desk has not been moved. He then checks that talcum powder on a cupboard handle is free of fingerprints. Lastly, he confirms that the water level in the lavatory water cistern hasn’t changed. Satisfied, he settles down to contemplate his larger mission.
Today, Bond would not find it so easy to be sure of his privacy. His secrets would be stored not in rooms, but on computers. And when he needed to share those secrets in the safest modern way, he would rely on complicated devices that use quantum physics, the science of the small. These devices look like Jenga puzzles, full of valves, chambers, lasers and lenses. How on earth could Bond possibly be sure it was safe to use them?
“Quantum devices are very difficult to characterize. You don’t want to depend on the details,” said Mateus Araújo of the Austrian Academy of Sciences. “If you do, then you are vulnerable to hacking.”
But almost from the devices’ conception three decades ago, there were hints that these vulnerabilities might not be a problem. Theorists went on to prove that, amazingly, all the users had to do to ensure privacy was to have the devices play a game. Simply winning — with a high enough score — would prove that no one else could be listening.
Now, two different experiments based in Oxford and Munich have demonstrated this process, known as device-independent quantum key distribution. A third experiment, based in Shanghai, concurrently demonstrated many of the necessary requirements. Each of the three groups of researchers had to carefully engineer complete cryptographic systems out of quantum components.
“I’m extremely excited and happy to see them,” said Roger Colbeck of the University of York. “They are doing different things; each of them is individually a very impressive achievement.”
Their experiments lift the perfect secrecy inherent in the quantum realm — unknown and uncertain by nature — into the macroscopic world of the everyday. The technology is still too slow to be practical. Nevertheless, even the most paranoid now know it’s possible to communicate with perfect privacy.
The Key to Secrecy
The origins of the new work date back to 1949, when Claude Shannon proved that perfect secrecy was even possible.
Suppose you want to encrypt some information, represented as a sequence of bits (1s and 0s). You can add to it another sequence of bits — this one perfectly random — called a key. The combined sequence will now appear random and thus meaningless to any observer who does not also know the key.
The question became how to securely distribute the key to the people who need it — and how to do it in a timely way. “For this key to be useful, we need both of us to know the key, and we need no one else to be able to learn it,” said Rotem Arnon-Friedman of the Weizmann Institute of Science in Israel.
While you could simply write the key on a pad of paper and send it by courier, that only reframes the problem: How do you ensure the courier’s safety and speed? Over the next 30 years, cryptographers created nonrandom keys that could be distributed rapidly and securely. However, these new kinds of keys were not perfectly secure: They could be hacked with sufficient computing power. To reclaim perfection, cryptographers had to learn how to play a nonlocal game.
Quantum Coins
These games were originally invented by physicists to test whether the laws of quantum mechanics were real. Only later did Artur Ekert, a physicist at the University of Oxford, realize that they could serve as the source of secrecy.
The game that Ekert studied has two players, Alice and Bob, who are totally isolated from each other. In every round, each player is asked one of two yes-or-no questions at random. In order for them to win the round, their answers must correspond in the following specific ways. If they both get the first question, they must give the same answer. Likewise, if they get different questions, they must give the same answer. But if they both get the second question, they must give different answers to win.
How should Alice and Bob play the game to maximize their chances of winning? Since the questions are asked randomly, the chance that they will both be asked the second question (requiring different answers to win) is only 25%. Without doing anything quantum, then, the best strategy they could agree on in advance would be to always give the same answer, always yes or always no. If they do this, they will win, on average, 75% of the rounds.
Merrill Sherman for Quanta Magazine
But physicists figured out that Alice and Bob could do better by using quantum physics. Before separating, they would need to obtain a set of four quantum objects (such as atoms or particles), two for Alice and two for Bob. We can think of these objects as coins, because interacting with them produces one of two outcomes, heads or tails.
Then Alice and Bob must put the coins into a special relationship with each other, known as quantum entanglement. They entangle them in the following specific way: When Alice flips her first coin, Bob’s first coin is more likely to land on the same side when he flips his. And when they both flipped different coins, they are also more likely to land the same. But when Alice flips her second coin and Bob flips his second, they are more likely to land on different sides.
This, you may notice, corresponds with the win conditions for the game. Armed with their quantum coins, Alice and Bob flip their first or second coin in response to the first or second question, respectively, saying yes for heads and no for tails. By following the commands of the quantum coins, Alice and Bob could win about 85% at a maximum: a gambler’s dream.
“It follows from the laws of quantum mechanics,” said Colbeck. “You just work it out, and you get 85%. But there’s no good intuitive reason why it is that number.”
Merrill Sherman for Quanta Magazine
In 1991, Ekert showed that this game provided a basis for distributing keys. But theorists would spend 30 more years turning the game into a protocol, or detailed process, that they could mathematically prove to be secret — even for the improbable case where Alice and Bob used coins manufactured by their enemies.
Secret Process
To turn their game into a process for sharing keys, Alice and Bob must make a public announcement.
Every so often, after a round is over, they broadcast some of their questions and answers. This allows them to check their answers against their questions and figure out their winning percentage. If they find they have a win rate of 85% — the theoretical maximum — it establishes a set of extraordinary facts about the process that make perfect security possible.
First, it proves that the outcomes of the coin flips are random. How do they know?
Let’s say an eavesdropper named Eve tries to rig the coins to make them nonrandom — for example, altering Alice and Bob’s first coins so that they always land heads. That might seem like it would increase the win rate, but it doesn’t. If you systematically analyze the probabilities, you’ll find that no matter what Eve does, there’s no way she can rig the coins so that Alice and Bob win more than 75% of the time. Victory above 75% therefore signifies that nothing could have been rigged or prearranged.
“Something random is happening,” said Colbeck.
With their random flips, Alice and Bob can then create the random bits needed to form a key. For each coin flip that they did not publicly disclose, Alice and Bob mark a 1 for heads and a 0 for tails. This sequence is secret, known only to them. But because their coins are correlated, they have a good idea of the secret sequence the other person marks down as well. (They don’t know it perfectly, because their correlations do not reach all the way to 100%, but they can find it out by making only a slight modification to the game.)
At this point, Alice and Bob have distributed a random key. But a problematic possibility remains. Is it secret? Suppose Eve entangled two of her own coins with Alice and Bob’s before they began. Wouldn’t that allow her to share in the correlations, enabling her to create her own version of the same key?
Extraordinarily, the answer is no. Ekert realized that victory at 85% rules out the possibility that Eve (or anyone else) could be spying. That’s because quantum entanglement is “monogamous” — spreading it between more than two parties means it must be spread thinner. If Eve’s coins were also entangled with Alice and Bob’s, the correlation levels would drop, and their winning rate would dip below 85%. Which means that if they measure an 85% winning rate, Eve cannot possibly be listening in.
“If we get something close to the maximum,” said David Nadlinger of the University of Oxford, “the things that Eve could be listening in on are very small.”
These two qualities — randomness and privacy — establish that in principle, winning the game at 85% is all Alice and Bob need to do to distribute keys with perfect secrecy. But for cryptographers, who are paranoid by profession, things are not so simple. Foremost in their minds is the knowledge that winning the game with a score of 85% is impossible in the real world. After all, the coins are really quantum objects that must be manipulated with the help of complex machines. This makes them susceptible to countless errors and hacking strategies.
So theorists set out to prove that as long as Alice and Bob won more than the classical maximum of 75%, but less than the quantum maximum of 85%, perfect security could still be guaranteed. And they succeeded — but only in cases where the devices were suitably trustworthy, perhaps manufactured by a friend with assurances that they worked in certain ways (such as not having memory). By 2007, researchers began to successfully strip away those assumptions, showing that security was also possible for devices with fewer restrictions.
This research culminated in a result from 2018, which proved that security could be achieved with winning percentages that seemed low enough that experimentalists might be able to reach them, even if Eve made the devices herself. As long as the devices allowed Alice and Bob to win at a certain rate in the game, it was clear: They had obtained secrecy.
Flipping Particles
Two years ago, buoyed by the new results, each of the three groups of researchers decided that a demonstration of device-independent key distribution was now possible. They just had to do it.
They had already developed different ways of playing the game. In place of coins, the researchers involved in the Oxford experiment used ionized atoms, which they entangled at the start of each round. Once entangled, they flipped them by shooting the atoms with lasers and measuring whether they glowed or stayed dark — two different outcomes, just like heads or tails. They were able to reduce the complexity of their setup by using one single coin (or atom), instead of two, which they could flip (measure) in two different ways. The researchers running the Munich experiment used a similar setup, whereas the researchers in the Shanghai experiment went in a different direction, using photons as coins instead of atoms. For them, flipping an entangled photon and detecting it were the same thing.

At the University of Oxford, a vacuum chamber with an ion trapped inside plays the part of Bob’s quantum coin in a nonlocal game. Using it, and another machine, researchers successfully generated a full encryption key that they could prove to be perfectly secret.
David Nadlinger/University of Oxford
However, it was not enough to merely play the game. The experiments had to reliably achieve a high enough winning percentage. Only by meeting this requirement could they prove that the bits that they generated were truly secret.
Initially, the Munich experiment couldn’t reach the winning percentage that would prove the bits that they generated were secret. But the team eventually realized they could lower the percentage needed to win by changing their protocol, incorporating an additional flip into the game.
“By introducing more random measurement,” said Charles Lim of the National University of Singapore, “that randomness penalizes Eve more than before, and as a result, we can tolerate a lot more noise.”
The experiments also had to complete rounds quickly if they were to distribute a substantial number of key bits in a timely way. Here, the Chinese experiment had an advantage. They could generate their photons at high speeds. However, this made measuring the flip of each coin very difficult. It could lead to researchers missing flips, which would give Eve a powerful tactic that she could use to cheat, known as the detection loophole.
“Bob needs to keep everything, and make sure his [detector] efficiency is very high,” said Feihu Xu of the University of Science and Technology of China.
In part, the researchers involved in the Shanghai experiment overcame this problem by developing a new protocol that allowed them to provably generate secret bits of a key, even with lower detection efficiency. However, the new protocol that they created does not ensure perfect privacy when their devices have been manipulated by the most powerful adversaries.
In contrast, the Oxford and Munich experiments could prove that the bits generated in each round were secret, regardless of any possible tampering. However, the Oxford group sought to go one step further and distribute a full finite key, which has the highest possible standard of secrecy, even though making it requires hundreds of thousands of key bits. They therefore needed even more speed, which was limited by, among other things, the distance between Alice and Bob (and their atoms).
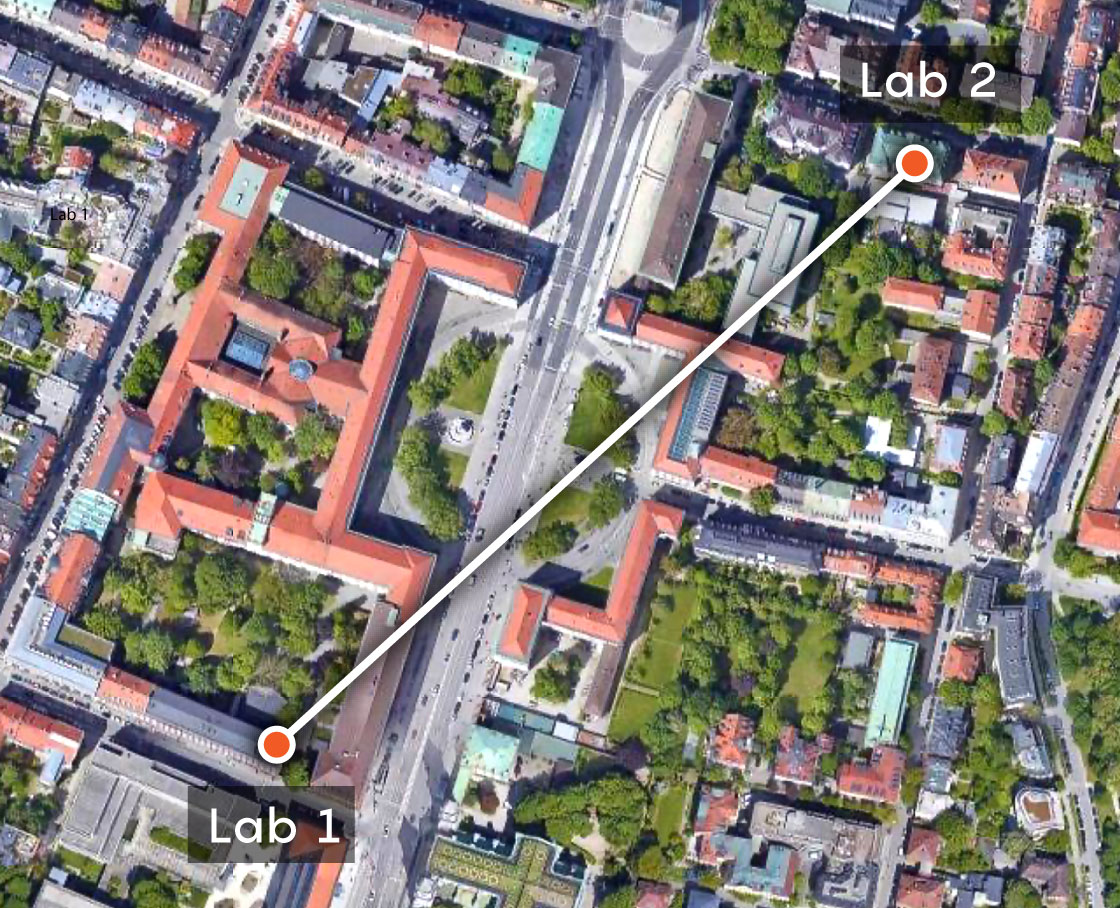
Researchers at the Ludwig Maximilian University of Munich distributed bits of an encryption key between two parties 400 meters apart.
Quanta Magazine; source: Tim van Leent
With a short distance setup, the Oxford experiment managed to generate over a million key bits during the course of a single day. They then developed and executed an extensive protocol to convert this large set of bits into a complete finite key.
“This finite data set analysis makes a massive difference in how you actually do stuff,” said Christopher Ballance of the University of Oxford. “And this is where a lot of the work went in.”
Altogether, the experiments show that we have entered an age in which the complexity of our quantum devices no longer presents an obstacle to sharing perfect secrets.
The Secrecy of Reality
Despite their achievements, all three experiments are still just a start. They struggle to generate and distribute keys at practical speeds, and at a considerable distance. Each group is actively working on improving in both areas.
“We need to continue to advance the technology to get significantly higher key rates,” said Arnon-Friedman. “We’re still looking for a game-changing technology.”
Long before we reach that point, the experiments will have already signified a substantial shift in the practicality of nonlocal games. These were invented to investigate the exotic phenomenon of nonlocality — the way objects can be instantaneously correlated across arbitrary distances. Now, nonlocal games provide the foundation for a much more practical process, the generation of a shared secret key.
“I sometimes say tongue-in-cheek even God couldn’t know it. The universe hadn’t decided what the value would be before it was measured,” said Colbeck. “That’s the origin of the security.”



