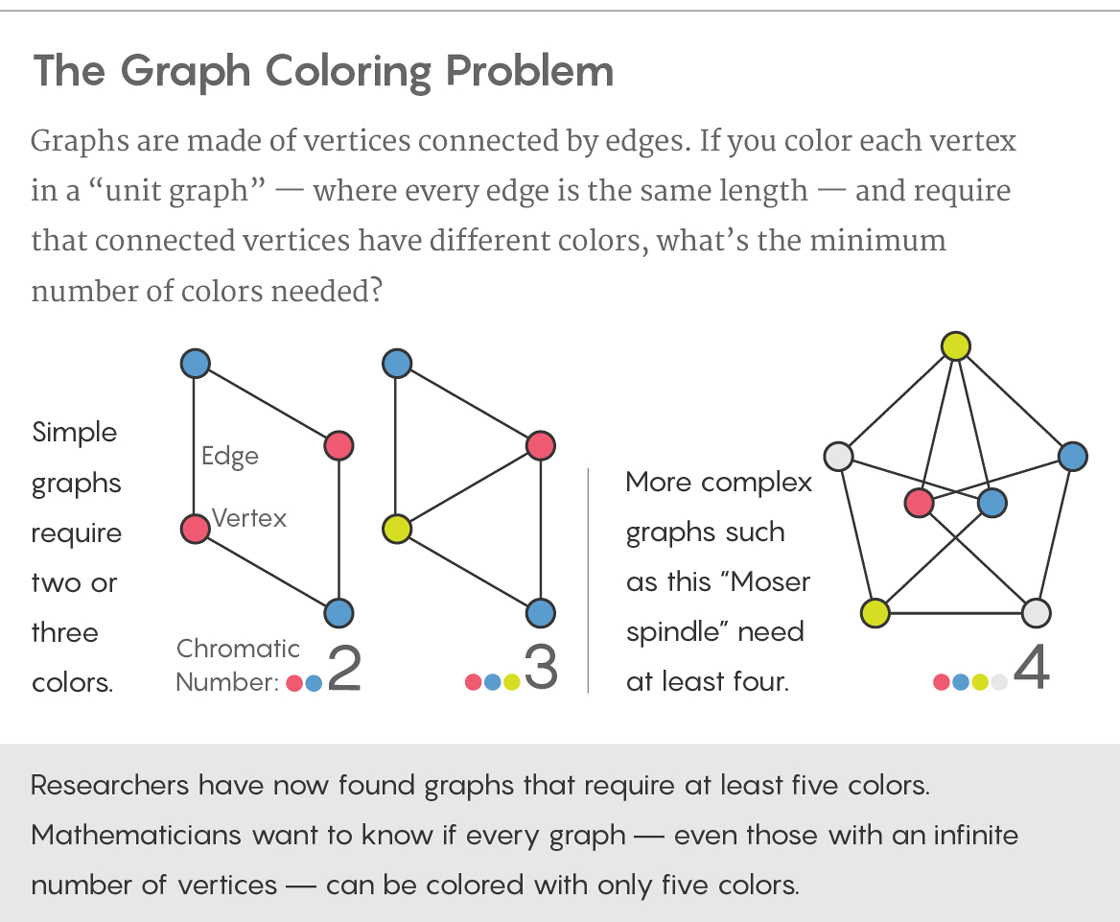
Decades-Old Graph Problem Yields to Amateur Mathematician


This 826-vertex graph requires at least five colors to ensure that no two connected vertices are the same shade. (Click here for a high-resolution version.)
Olena Shmahalo/Quanta Magazine; Source: Marijn Heule
Introduction
In 1950 Edward Nelson, then a student at the University of Chicago, asked the kind of deceptively simple question that can give mathematicians fits for decades. Imagine, he said, a graph — a collection of points connected by lines. Ensure that all of the lines are exactly the same length, and that everything lies on the plane. Now color all the points, ensuring that no two connected points have the same color. Nelson asked: What is the smallest number of colors that you’d need to color any such graph, even one formed by linking an infinite number of vertices?
The problem, now known as the Hadwiger-Nelson problem or the problem of finding the chromatic number of the plane, has piqued the interest of many mathematicians, including the famously prolific Paul Erdős. Researchers quickly narrowed the possibilities down, finding that the infinite graph can be colored by no fewer than four and no more than seven colors. Other researchers went on to prove a few partial results in the decades that followed, but no one was able to change these bounds.
Then last week, Aubrey de Grey, a biologist known for his claims that people alive today will live to the age of 1,000, posted a paper to the scientific preprint site arxiv.org with the title “The Chromatic Number of the Plane Is at Least 5.” In it, he describes the construction of a unit-distance graph that can’t be colored with only four colors. The finding represents the first major advance in solving the problem since shortly after it was introduced. “I got extraordinarily lucky,” de Grey said. “It’s not every day that somebody comes up with the solution to a 60-year-old problem.”

Aubrey de Grey came up with the first unit-distance graph that requires at least five colors.
Courtesy of Aubrey de Grey/SENS Research Foundation
De Grey appears to be an unlikely mathematical trailblazer. He is the co-founder and chief science officer of an organization that aims to develop technologies for “reversing the negative effects of aging.” He found his way to the chromatic number of the plane problem through a board game. Decades ago, de Grey was a competitive Othello player, and he fell in with some mathematicians who were also enthusiasts of the game. They introduced him to graph theory, and he comes back to it now and then. “Occasionally, when I need a rest from my real job, I’ll think about math,” he said. Over Christmas last year, he had a chance to do that.
It is unusual, but not unheard of, for an amateur mathematician to make significant progress on a long-standing open problem. In the 1970s, Marjorie Rice, a homemaker with no mathematical background, ran across a Scientific American column about pentagons that tile the plane. She eventually added four new pentagons to the list. Gil Kalai, a mathematician at the Hebrew University of Jerusalem, said it is gratifying to see a nonprofessional mathematician make a major breakthrough. “It really adds to the many facets of the mathematical experience,” he said.
Perhaps the most famous graph coloring question is the four-color theorem. It states that, assuming every country is one continuous lump, any map can be colored using only four colors so that no two adjacent countries have the same color. The exact sizes and shapes of the countries don’t matter, so mathematicians can translate the problem into the world of graph theory by representing every country as a vertex and connecting two vertices with an edge if the corresponding countries share a border.
Lucy Reading-Ikkanda/Quanta Magazine
The Hadwiger-Nelson problem is a bit different. Instead of considering a finite number of vertices, as there would be on a map, it considers infinitely many vertices, one for each point in the plane. Two points are connected by an edge if they are exactly one unit apart. To find a lower bound for the chromatic number, it suffices to create a graph with a finite number of vertices that requires a particular number of colors. That’s what de Grey did.
De Grey based his graph on a gadget called the Moser spindle, named after mathematical brothers Leo and William Moser. It is a configuration of just seven points and 11 edges that has a chromatic number of four. Through a delicate process, and with minimal computer assistance, de Grey fused copies of the Moser spindle and another small assembly of points into a 20,425-vertex monstrosity that could not be colored using four colors. He was later able to shrink the graph to 1,581 vertices and do a computer check to verify that it was not four-colorable.

De Grey’s 1,581-vertex graph. (Click here for a high-resolution version.)
Olena Shmahalo/Quanta Magazine; Source: Aubrey de Grey
The discovery of any graph that requires five colors was a major accomplishment, but mathematicians wanted to see if they could find a smaller graph that would do the same. Perhaps finding a smaller five-color graph — or the smallest possible five-color graph — would give researchers further insight into the Hadwiger-Nelson problem, allowing them to prove that exactly five shades (or six, or seven) are enough to color a graph made from all the points of the plane.
De Grey pitched the problem of finding the minimal five-color graph to Terence Tao, a mathematician at the University of California, Los Angeles, as a potential Polymath problem. Polymath began about 10 years ago when Timothy Gowers, a mathematician at the University of Cambridge, wanted to find a way to facilitate massive online collaborations in mathematics. Work on Polymath problems is done publicly, and anyone can contribute. Recently, de Grey was involved with a Polymath collaboration that led to significant progress on the twin prime problem.
Tao says not every math problem is a good fit for Polymath, but de Grey’s has a few things going for it. The problem is easy to understand and start working on, and there is a clear measure of success: lowering the number of vertices in a non-four-colorable graph. Soon enough, Dustin Mixon, a mathematician at Ohio State University, and his collaborator Boris Alexeev found a graph with 1,577 vertices. On Saturday, Marijn Heule, a computer scientist at the University of Texas, Austin, found one with just 874 vertices. Yesterday he lowered this number to 826 vertices.
Such work has sparked hope that the six-decade-old Hadwiger-Nelson problem is worth another look. “For a problem like this, the final solution might be some incredibly deep mathematics,” said Gordon Royle, a mathematician at the University of Western Australia. “Or it could just be somebody’s ingenuity finding a graph that requires many colors.”
Correction April 20, 2018: The original version of this article reported that de Grey had found a “planar unit-distance graph.” In graph theory, “planar” means that a graph can be embedded in the plane in such a way that its edges never cross. De Grey’s graph is instead a graph in the plane with edges of unit length, or just a “unit-distance graph.”
This article was reprinted on Wired.com.






