How Public Key Cryptography Really Works, Using Only Simple Math

For thousands of years, if you wanted to send a secret message, there was basically one way to do it. You’d scramble the message using a special rule, known only to you and your intended audience. This rule acted like the key to a lock. If you had the key, you could unscramble the message; otherwise, you’d need to pick the lock. Some locks are so effective they can never be picked, even with infinite time and resources. But even those schemes suffer from the same Achilles’ heel that plagues all such encryption systems: How do you get that key into the right hands, while keeping it out of the wrong ones?

The counterintuitive solution, known as public key cryptography, relies not on keeping a key secret, but rather on making it widely available. The trick is to also use a second key that you never share with anyone, even the person you’re communicating with. It’s only by using this combination of two keys — one public, one private — that someone can both scramble and unscramble a message.

To understand how this works, it’s easier to think of the “keys” not as objects that fit into a lock, but as two complementary ingredients in an invisible ink. The first ingredient makes messages disappear, and the second makes them reappear. If a spy named Boris wants to send his counterpart Natasha a secret message, he writes a message and then uses the first ingredient to render it invisible on the page. (This is easy for him to do: Natasha has published an easy and well-known formula for disappearing ink.) When Natasha receives the paper in the mail, she applies the second ingredient that makes Boris’ message reappear.

In this scheme, anyone can make messages invisible, but only Natasha can make them visible again. And because she never shares the formula for the second ingredient with anyone — not even Boris — she can be sure the message hasn’t been deciphered along the way. When Boris wants to receive secret messages, he simply adopts the same procedure: He publishes an easy recipe for making messages disappear (that Natasha or anyone else can use), while keeping another one just for himself that makes them reappear.

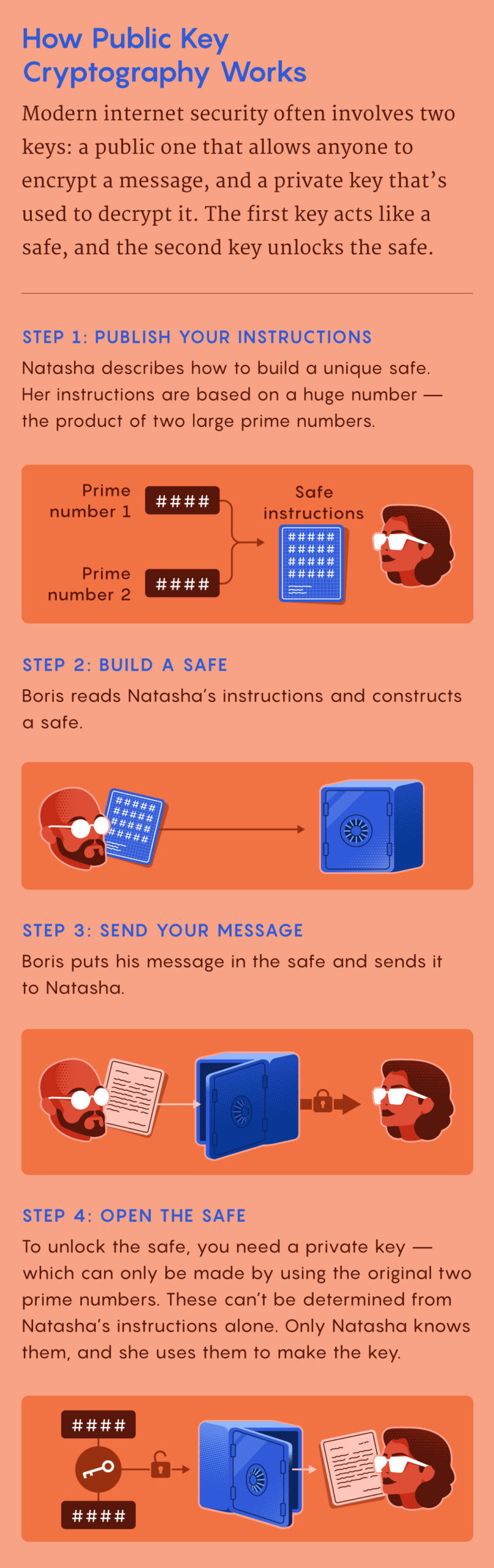
In public key cryptography, the “public” and “private” keys work just like the first and second ingredients in this special invisible ink: One encrypts messages, the other decrypts them. But instead of using chemicals, public key cryptography uses mathematical puzzles called trapdoor functions. These functions are easy to compute in one direction and extremely difficult to reverse. But they also contain “trapdoors,” pieces of information that, if known, make the functions trivially easy to compute in both directions.

One common trapdoor function involves multiplying two large prime numbers, an easy operation to perform. But reversing it — that is, starting with the product and finding each prime factor — is computationally impractical. To make a public key, start with two large prime numbers. These are your trapdoors. Multiply the two numbers together, then perform some additional mathematical operations. This public key can now encrypt messages. To decrypt them, you’ll need the corresponding private key, which contains the prime factors — the necessary trapdoors. With those numbers, it’s easy to decrypt the message. Keep those two prime factors secret, and the message will stay secret.

The foundations for public key cryptography were first discovered between 1970 and 1974 by British mathematicians working for the U.K. Government Communications Headquarters, the same government agency that cracked the Nazi Enigma code during World War II. Their work (which remained classified until 1997) was shared with the U.S. National Security Agency, but due to limited and expensive computing capacity, neither government implemented the system. In 1976, the American researchers Whitfield Diffie and Martin Hellman discovered the first publicly known public key cryptography scheme, influenced by the cryptographer Ralph Merkle. Just a year later, the RSA algorithm, named after its inventors Ron Rivest, Adi Shamir and Leonard Adleman, established a practical way to use public key cryptography. It’s still in wide use today, a fundamental building block of the modern internet, enabling everything from shopping to web-based email.

This two-key system also makes possible “digital signatures” — mathematical proof that a message was generated by the holder of a private key. This works because private keys can be used to encrypt messages too, not just decrypt them. Of course, this is useless for keeping messages secret: If you used your private key to scramble a message, anyone could just use the corresponding public key to unscramble it. But it does prove that you, and only you, created the message, since as the holder of the private key, only you could have encrypted the message. Cryptocurrencies like bitcoin couldn’t exist without this idea.

If two cryptographic keys instead of one is so effective, why did it take millennia to discover? According to Russell Impagliazzo, a computer scientist and cryptography theorist at the University of California, San Diego, the concept of a trapdoor function just wasn’t useful enough before the invention of computers.

“It’s a matter of technology,” he said. “A person in the 19th century thought of encryption as being between individual agents with military intelligence in the field — literally, in a field with guns firing. So if your first step is ‘pick two 100-digit prime numbers to multiply together,’ the battle is going to be over before you do that.” If you reduce the problem to something a human can do quickly, it’s not going to be terribly secure.

But while computers helped make public key cryptography possible, they’ve also created cracks in its armor. In 1994, the mathematician Peter Shor discovered a way for quantum computers to efficiently reverse the trapdoor functions that underlie most current public key cryptography systems, including prime factorization. This algorithm, if implemented, would act like an all-purpose “reappearing ink,” capable of making any invisible message reappear. Goodbye, internet security.

Luckily, quantum computers themselves are “still in the ENIAC phase,” Impagliazzo said, referring to the room-size machine built for the U.S. Army in 1945. By the time quantum computers become sophisticated enough to pose a real threat to public key cryptography, its original trapdoor functions could be replaced by “quantum-safe” versions called lattice problems. Of course, this new computational “ink” may also become susceptible to attack in the future. But that’s the great thing about public key cryptography: As long as we can find new functions to use, we can just keep reinventing the wheel. Or in this case, the key.