How Simple Math Can Cover Even the Most Complex Holes

“Hey — I’ve got holes in some of my jeans. Can you patch them for me?” Your friend, who knows of your legendary skill with a needle and thread, is texting you for help.

“Sure, that’s easy,” you reply. “How big are the holes?”

“They’re all weird shapes, but never wider than an inch. I’ll be by later, so get things ready!”

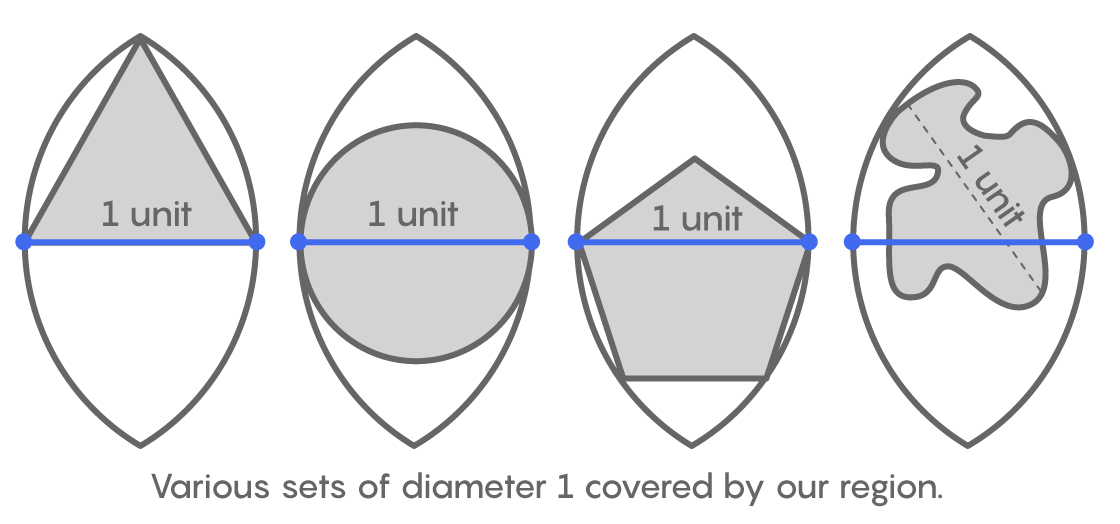
You go to your sewing kit and pull out some circular patches, each 1 inch in diameter. “This should do the trick,” you think to yourself. But will it? Can a circular patch of diameter 1 really cover any hole that is at most 1 inch wide in any direction?

You see a different patch in your kit, an equilateral triangle with 1-inch sides. You observe that no two points in the triangle are more than 1 inch apart, so a hole in your friend’s jeans might be this shape. But when you hold a circular patch against it, you notice that the circle covers two vertices of the triangle, but the third vertex sticks out.

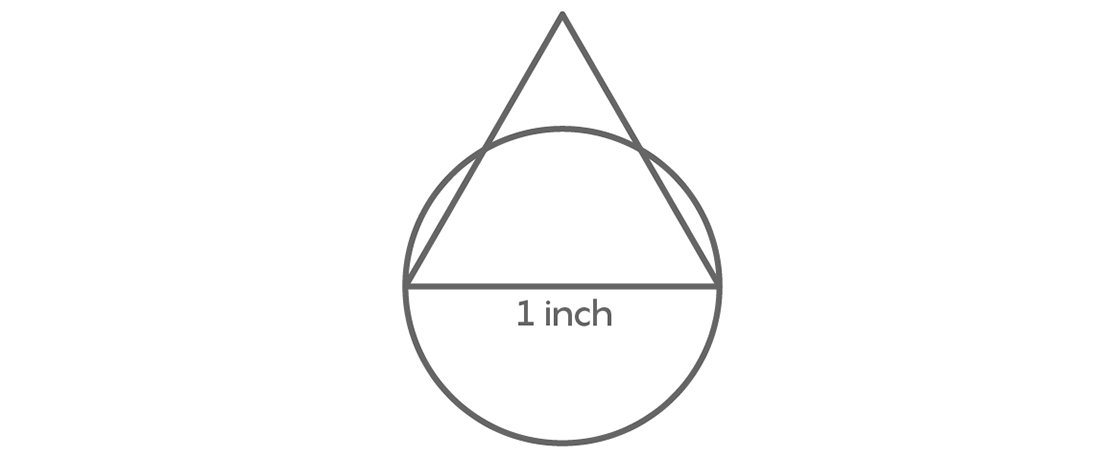
Some elementary geometry confirms that the height of the triangle, $latex \frac{\sqrt{3}}{2}$ inches, is greater than the circle’s radius, $latex \frac{1}{2}$ inch. The circle can’t cover the triangle, and the triangle can’t cover the circle either. Since a hole might be either shape, this means neither of these patches could cover every possible hole in your friend’s jeans.

You could just use a really big patch to be safe, but you don’t want to waste precious material. So the question is: What’s the smallest patch needed to cover a hole at most 1 inch wide? An online search reveals that mathematicians have been thinking about this question too: They’ve been searching for a minimal universal cover for more than 100 years. They haven’t found it yet, but recent results are getting us closer to this ideal shape.

The “universal covering problem” was first posed by Henri Lebesgue in a letter to his fellow mathematician Julius Pál in 1914. The problem can be formulated in different ways, but at its heart is the notion of a region of diameter 1: This is a set of points in the plane where no two points are more than 1 unit apart, like a hole no more than 1 inch wide in our pants patching problem.

If one set of points can fit inside another, we say the second set “covers” the first, like a patch that covers a hole. A “universal cover” is a region that can cover an entire set of shapes, like all the shapes of diameter 1, and Lebesgue’s universal covering problem asks for the smallest convex region that does the trick. (“Convex” roughly means that the cover has no indentations, and “smallest” means of minimal area.)

It may surprise you that such a seemingly elementary geometry problem hasn’t been solved in 100 years. But part of what makes the problem so difficult is that it’s hard to pin down exactly what a shape of diameter 1 could look like. As we’ve seen before, it can be hard to prove theorems about things you can’t entirely imagine.

When it comes to covering sets of diameter 1, there are plenty of shapes that we know work, just no shape we know is minimal. Let’s take a look at why mathematicians are having a hard time sewing this one up.

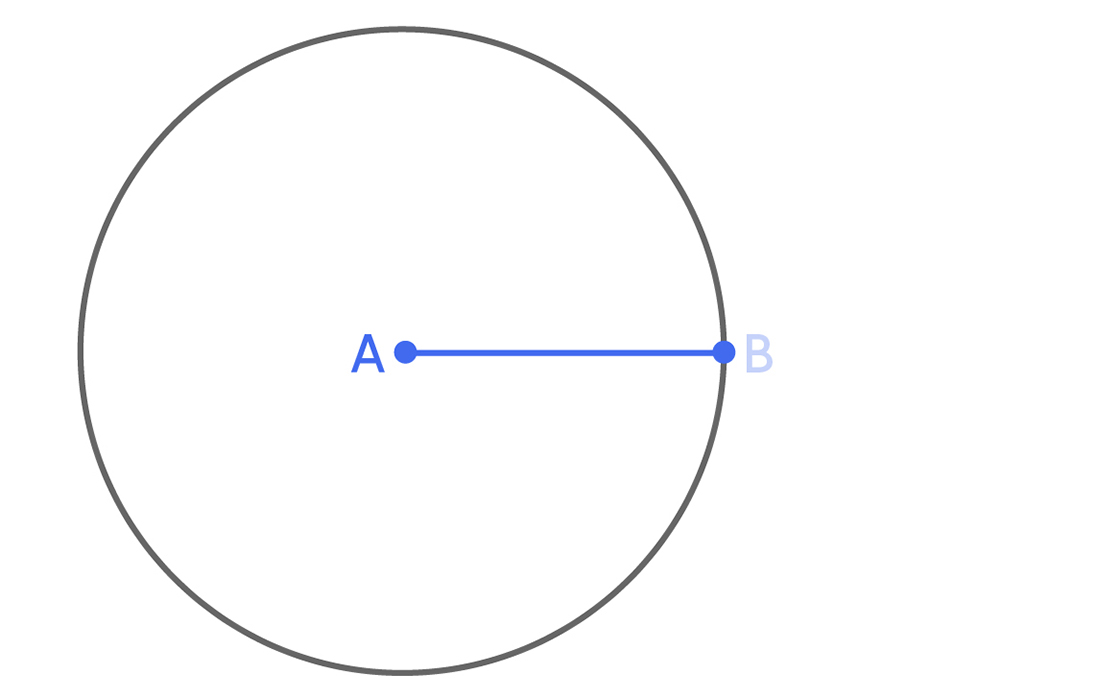
Let’s start with a region R of diameter 1. We really have no idea what R might look like; we only know that, just like the holes we’re trying to cover, it’s never more than 1 unit wide. But since it has diameter 1, let’s assume it has two points A and B that are 1 unit apart.

Now suppose R contains a third point C. Where could C be located? It can’t be more than 1 unit from A, which means it must be in the disk of radius 1 centered at A. You can construct this disk using a geometric compass centered at A and opened to B.

But C can’t be more than 1 unit from B, either, so it must be in the disk of radius 1 centered at B, which you can construct using your compass.

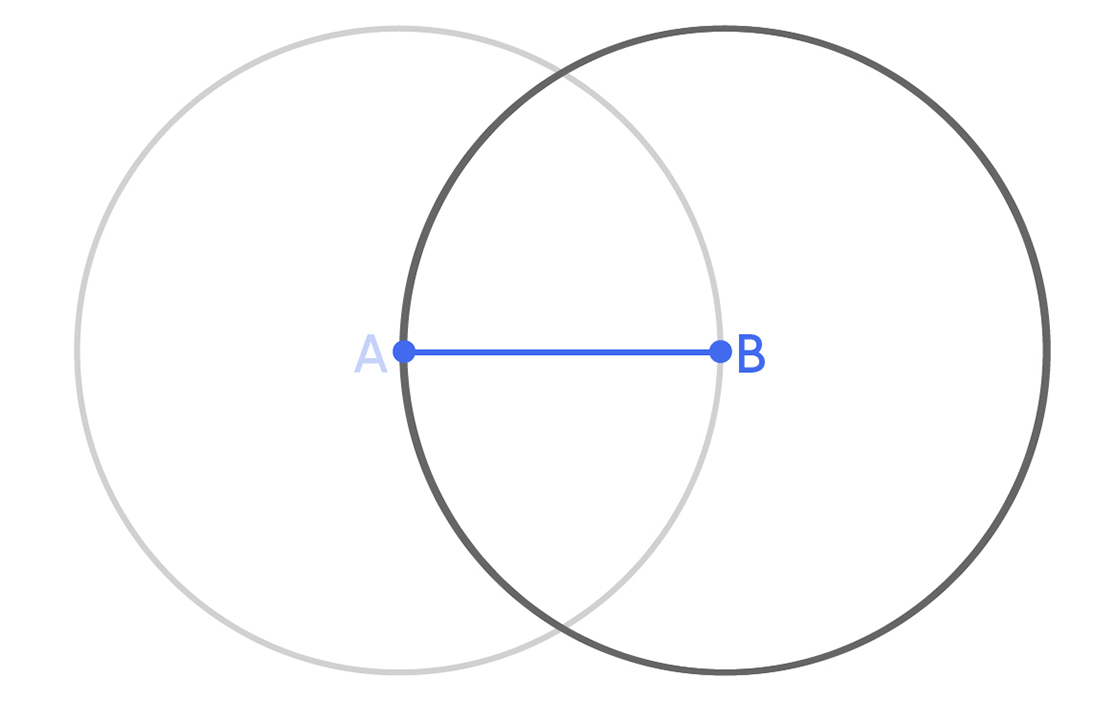
This means point C has to lie in the intersection of those two disks.

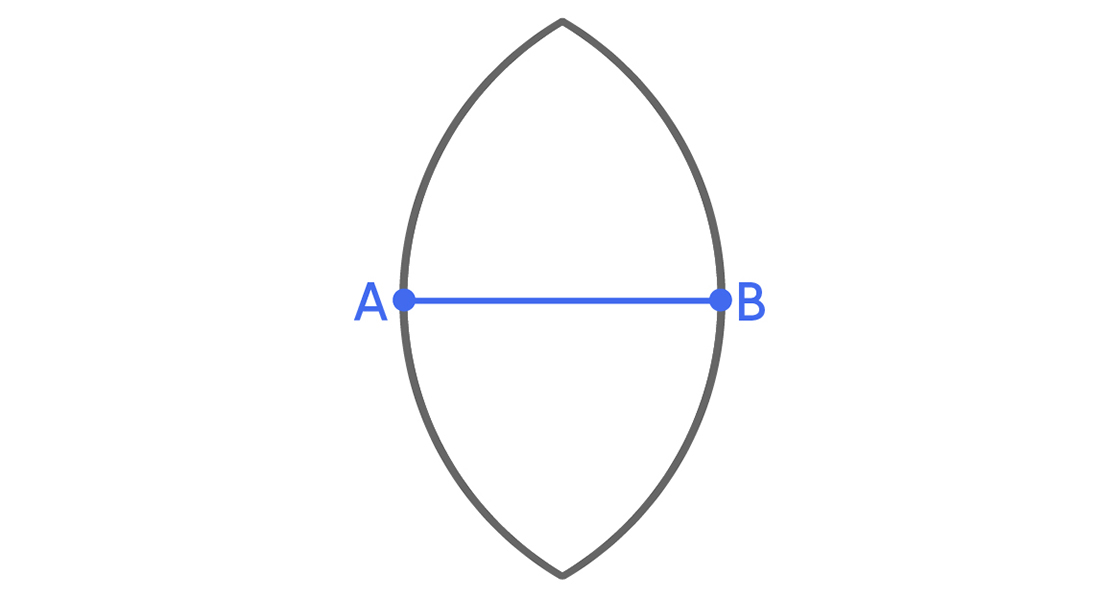
This argument doesn’t just apply to point C; it applies to every possible point in R. So every point in R must lie in the intersection of these two circles. In other words, this region can cover every possible set R of diameter 1 and is a universal cover.

But this universal cover doesn’t have minimal area. Let’s trim it down.

Notice that the intersecting points of the circles form two equilateral triangles with A and B, and the distance from the top (and the bottom) to the middle of segment AB is $latex \frac{\sqrt{3}}{2}$ units.

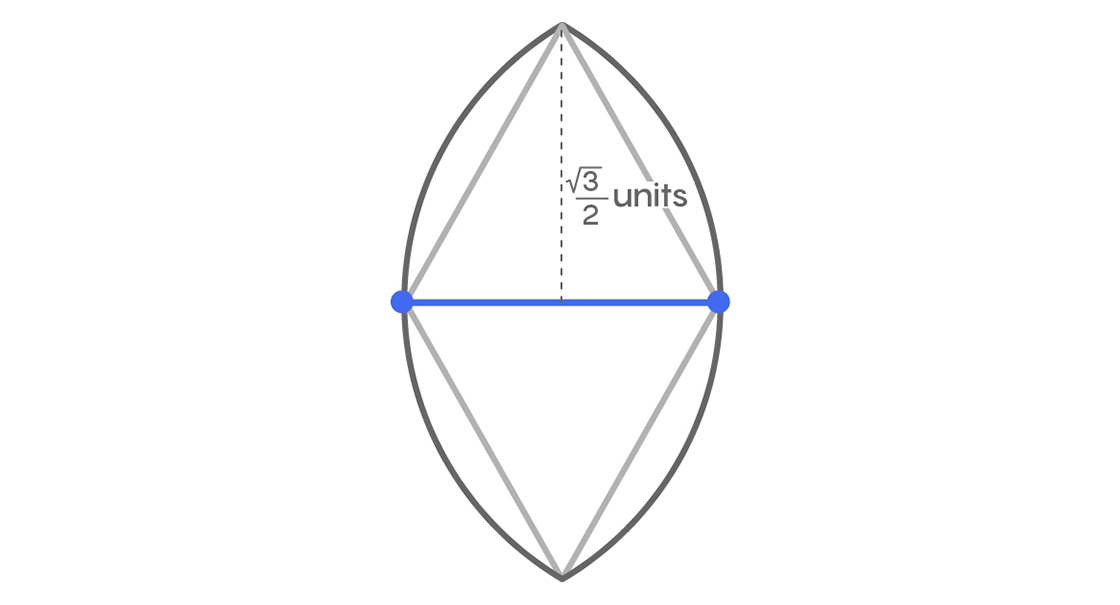
Since $latex \frac{\sqrt{3}}{2} > \frac{1}{2}$ , we can draw parallel lines $latex \frac{1}{2}$ unit away from $latex \overline{AB}$ on either side like this.

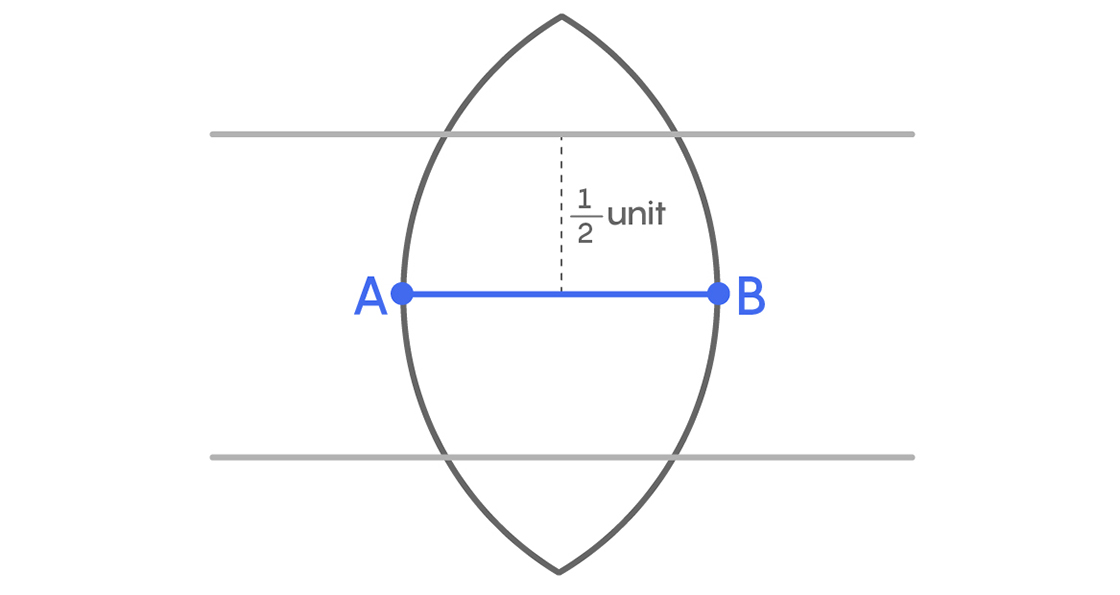
Now consider the two regions in red, one above the top parallel line and the other below the bottom one.

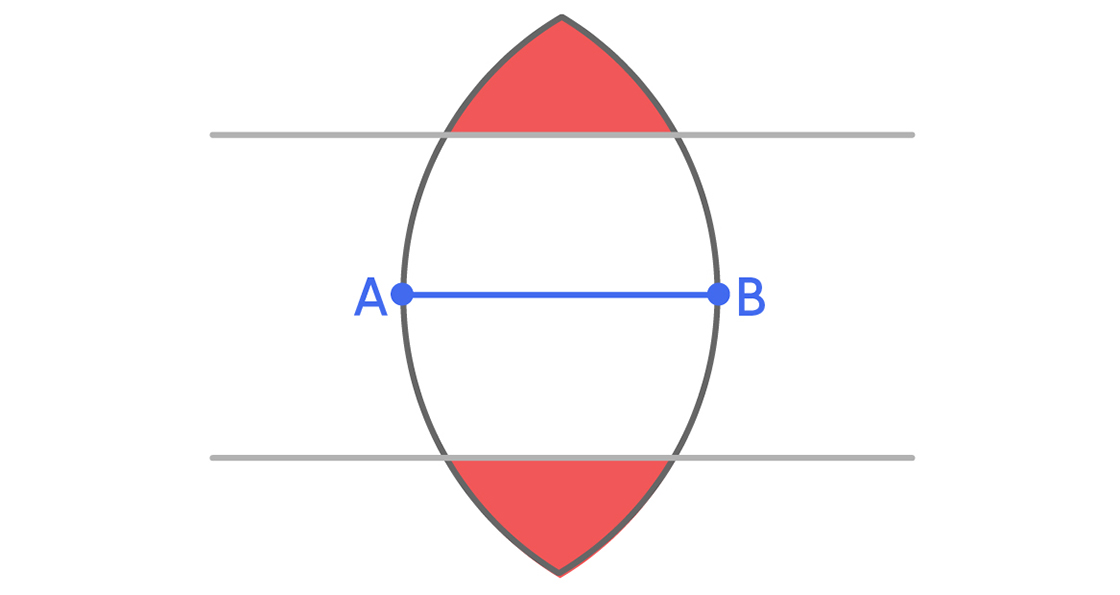
Since the distance between the two parallel lines is 1, a set of diameter 1 couldn’t possibly be in both red regions at the same time. That means we don’t need both red parts for a universal cover. We can just chop one off.

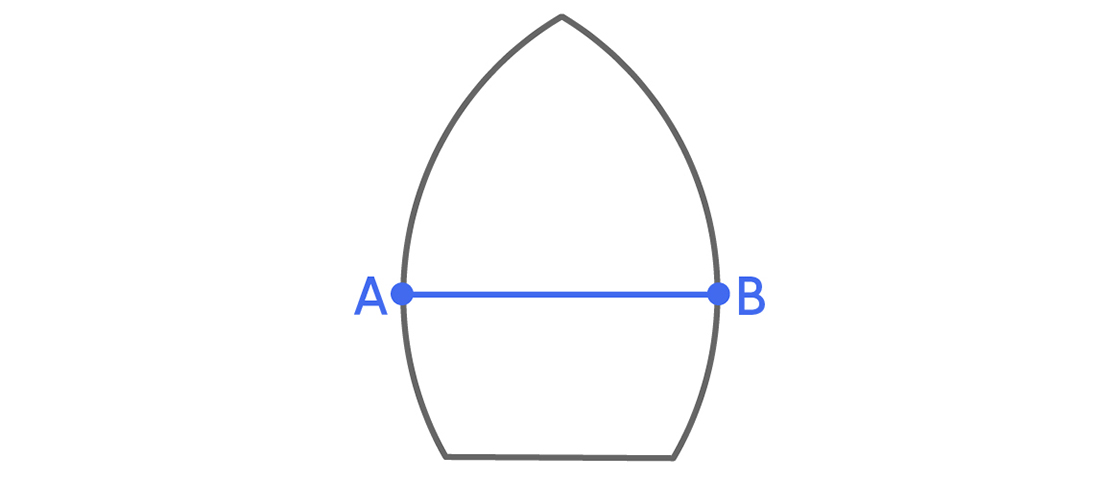
Our original cover — the intersection of the two disks — has area $latex \frac{2\pi}{3}-\frac{\sqrt{3}}{2} \approx$ 1.228, and our new cover has area $latex \frac{\pi}{2}-\frac{1}{2} \approx$ 1.071. Starting with an elementary universal cover, we were able to make it smaller by removing an extraneous piece.

This is exactly how mathematicians have arrived at the current smallest universal cover. Using more advanced techniques, we can find other simple shapes to start with. For example, it can be shown that a 1-by-1 square is a universal cover. And in response to Lebesgue’s challenge, Pál used properties of so-called curves of constant width to show that even though a set of diameter 1 might poke out of a circle of diameter 1, it can always be shifted or rotated to fit inside the hexagon that circumscribes that circle:

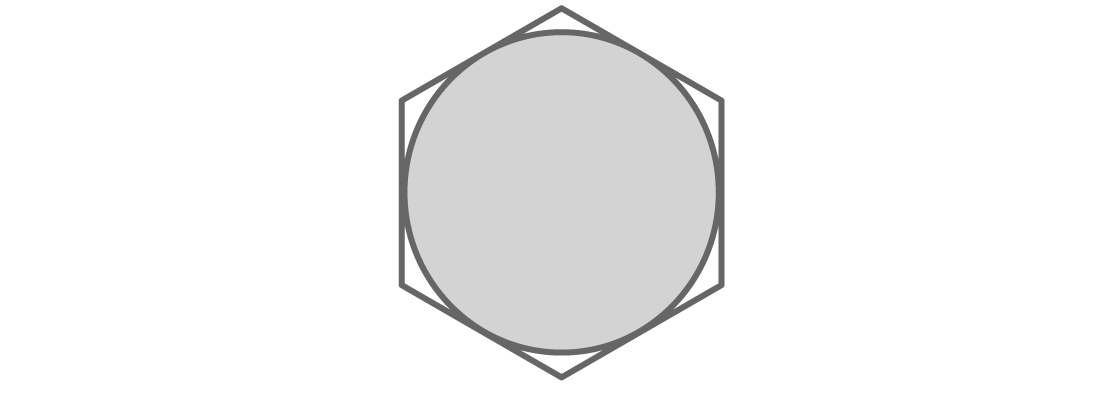
Below we show Pál’s hexagon covering various shapes of diameter 1. The shape in the middle is a Reuleaux triangle, a curve of constant width closely related to the example covers we constructed above. (We can construct a Reuleaux triangle from our example covers by centering our compass at the top intersection of the two circles, opening it to a width of 1, and making an arc from A to B.)

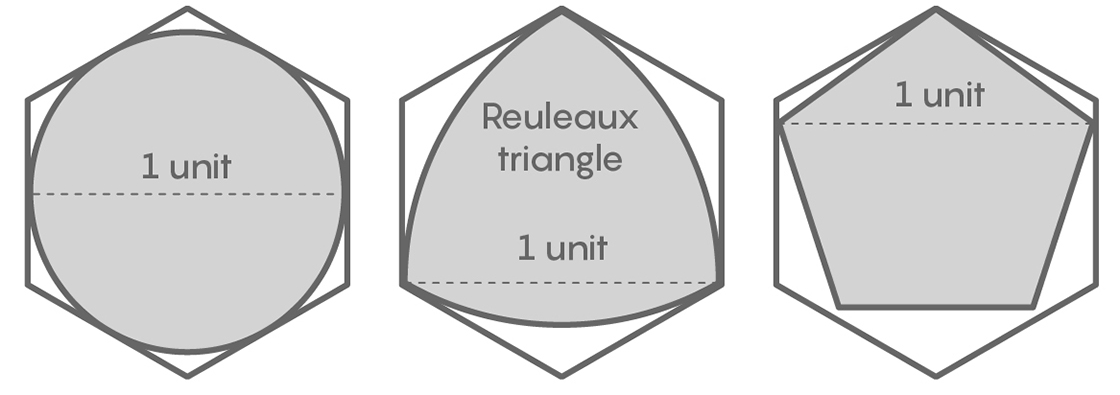
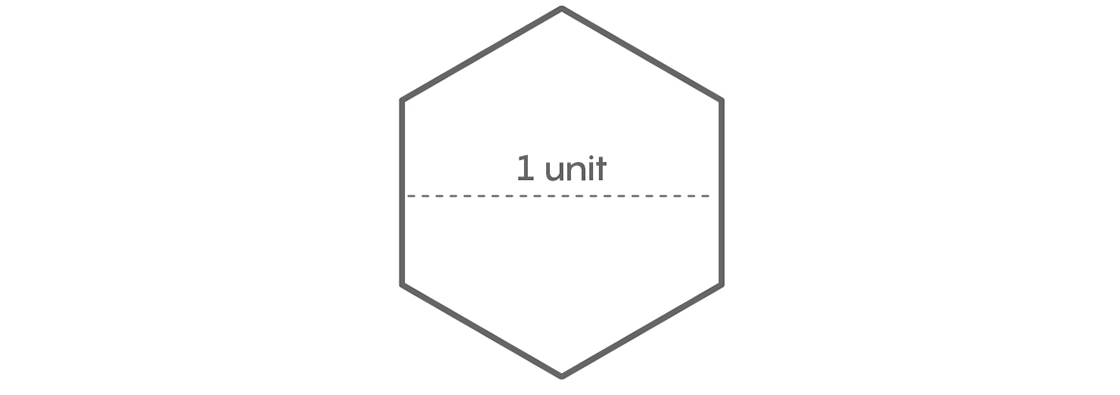
This hexagon has area $latex \frac{\sqrt{3}}{2} \approx$ 0.866, which is less than the area of our example covers and the unit square. But Pál also showed that we don’t need the entire hexagon. Using the following ingenious argument, he found some extraneous parts he could cut off.

Start with two copies of Pál’s hexagon stacked on top of each other

and rotate one of them 30 degrees about their center.

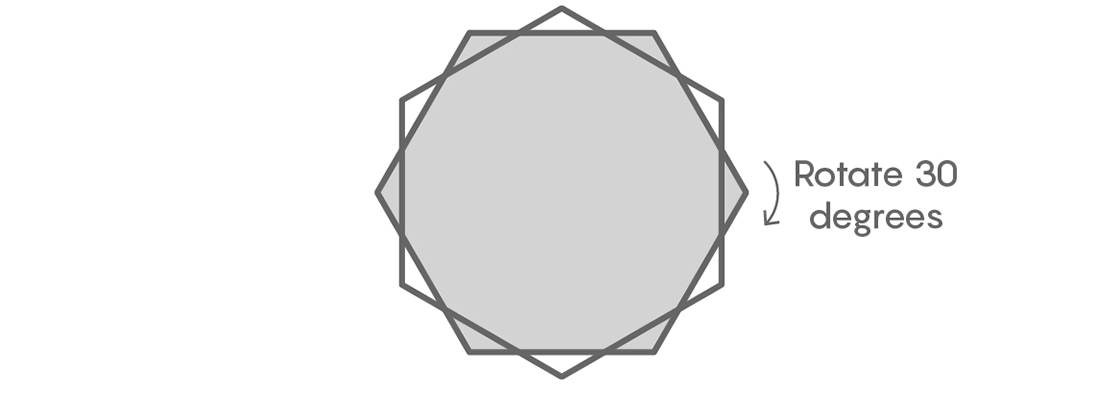
Lots of cool things are created by this — like a dodecagon formed by the intersection of the two hexagons — but we are most interested in the six little red triangles shown below.

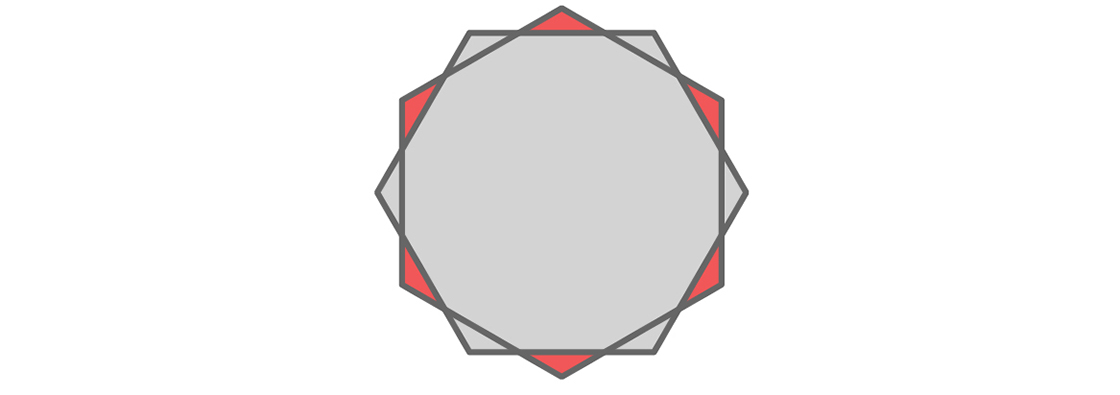
Each red triangle is both inside the original hexagon and outside the rotated hexagon. Since each pair of opposite sides of each hexagon are 1 unit apart, points lying in two opposing red triangles must be more than 1 unit apart. As in our argument above, a universal cover wouldn’t need both triangles in each opposing pair, since a set of diameter 1 couldn’t be in both at the same time. That means we should be able to remove some of them. Optimistically we might hope to remove three: one from each pair. But unfortunately we can’t remove three red triangles from our cover and still handle all possible sets of diameter 1. Let’s see why.

A hexagon can be rotated by 60 degrees or flipped across one of its lines of symmetry without anything changing, so there are really only two different ways to choose one red triangle from each opposing pair: The three triangles could be consecutive or they could alternate. This is shown below, with dots indicating which triangles a set of diameter 1 might occupy.

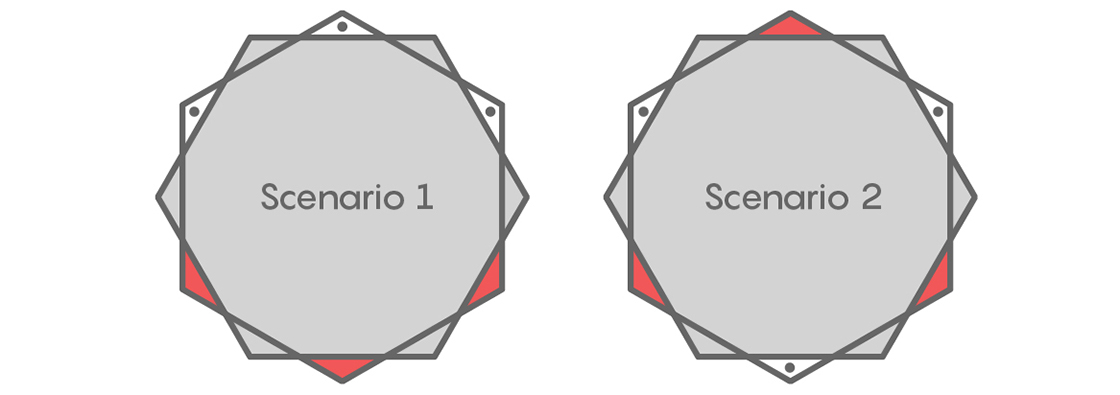
If the set we need to cover occupies three consecutive triangles, like on the left, it can’t be covered by the shape we’d get by removing three alternating triangles, like on the right. And if the set occupies three alternating triangles, it can’t be covered by the shape we’d get by removing three consecutive triangles. Removing either set of three triangles leaves a potential set of diameter 1 uncovered. So we can’t remove three red triangles.

But we can remove two. The two problematic sets described above can still be covered if we remove two red triangles that are neither adjacent nor opposite. That’s just what Pál did.

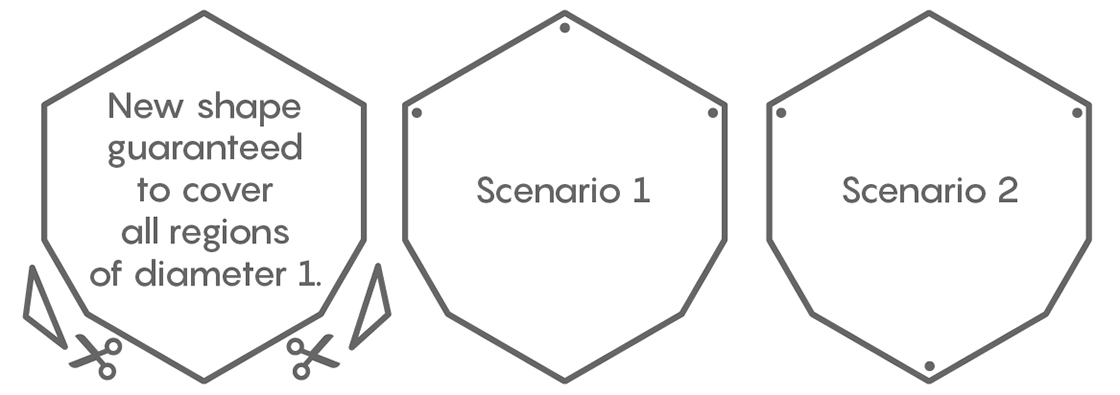
He sliced two triangles off his hexagon to get a new shape that is guaranteed to cover all regions of diameter 1. This new universal cover has an area of 2 – $latex \frac{2}{\sqrt{3}} \approx$ 0.8453 , slightly less than the hexagon.

And the trimming continued. Smaller pieces were successfully removed by the mathematicians Roland Sprague in 1936 and H.C. Hansen in 1992. And just a few years ago, the amateur mathematician Philip Gibbs, inspired by a blog post from the mathematician John Baez, proposed some new pieces to cut off. Working with Baez and another collaborator, he generalized the techniques of Sprague and Hansen to slice even more off the cover, claiming a new world record for the smallest convex cover of sets of diameter 1, a record Gibbs himself quickly improved upon by removing even more unnecessary area.

The good news is that we keep finding pieces of Pál’s hexagon to chop off. The bad news is that the pieces are very small. Sprague’s work reduced the cover’s area by about 0.001 square units, and Hansen’s only reduced it by 0.00000000004 square units. Gibbs and his collaborators reduced Hansen’s cover by around 0.00002 square units, which seems like a huge cut in comparison.

How low can they go? In 2005 Peter Brass and Mehrbod Sharifi proved that no universal cover could be smaller than 0.832 square units, so we know that we can’t chop too much more off the current record. But if you can come up with a new technique or a new starting point, you might get us closer to the minimal universal cover and slice off a piece of mathematical history for yourself. Just remember, the hardest part is imagining the infinitely many ways a set of diameter 1 could take shape. And making sure you’ve got all the possibilities covered.