How the Ancient Art of Eclipse Prediction Became an Exact Science
Introduction
Solar eclipses were interpreted throughout much of history as bad news for the sovereign — an ominous sign for their personal health or that of the realm. But those fears helped fuel thousands of years of scholarship. This progress began in Mesopotamia with a hunt for periodic patterns in historical data. It has culminated in an era in which we know the interdependent future motions of solar system bodies centuries in advance, transforming what was once a cause for cosmic-scale angst into a matter of cold clockwork.
If you had to pick one turning point, it might have been the morning of April 22, 1715, when a solar eclipse loomed over London. The British polymath Edmond Halley, best remembered as the namesake of Halley’s comet, had foretold it. He’d published a broadsheet that included a map of the path that the moon’s shadow would draw over England. That year, England had a freshly crowned king with a rebellion already brewing against him; by demystifying the eclipse with a prediction, Halley hoped to neutralize its power as an omen.
He also wanted to recruit data gatherers whose observations might lead to even better eclipse predictions going forward. “The Curious are desired to Observe it, and especially the duration of Total Darkness,” he advertised, “… for therby the Situation and dimensions of the Shadow will be nicely determin’d; and by means therof, we may be enabled to Predict the like Appearances for [the] future, to a greater degree of certainty than can be pretended to at present.”
Omens That Keep the Beat
Decades earlier, Halley, an avid reader of ancient texts, had rediscovered and popularized a helpful celestial cycle for thinking about eclipses and the position of the moon in the sky: 6,585 days, or a little more than 18 years. He called this cycle the “Saros,” which modern historians view as a mistranslation of a Sumerian symbol that originally meant something like “universe” or “big number.”
By around 600 BCE in Mesopotamia, Assyrian and Babylonian priest-mathematicians had scoured through the dates of past eclipses recorded in clay tablets, hoping to develop strategies for inferring when the next eclipse might happen. Eclipses worried kings in these cultures, and soon, with the invention of the zodiac and personal horoscopes, the need to keep tabs on the positions of the sun, moon and planets would concern everyone.
The first solutions were rules of thumb. Lunar eclipses often followed each other after six months, for example. The Babylonians also realized that specific solar and lunar eclipses were often separated from a similar event by what Halley called one Saros.
To understand this cycle in modern terms, imagine the geometry of celestial bodies at the moment of a solar eclipse, when the moon lies directly between the sun and Earth and all three bodies form a neat line. For this to happen, the moon must be a new moon. It must also be at a point where its own tilted orbit around the Earth is plunging through the plane in which the Earth marches through its own orbit around the sun.
Now imagine advancing the clock forward to find a time when these same conditions recur. We have to reconcile several overlapping but unequal lunar cycles. Cycle one: It takes about 29.5306 days to go from one new moon to the next. Cycle two: It takes the moon about 27.2122 days to go from one pass through the plane of Earth’s orbit to the same pass on the next go-round. Cycle three: Because the moon’s elliptical orbit draws it nearer and farther away from Earth, the moon also oscillates its apparent size and speed in the skies over Earth, a cycle that takes about 27.5546 days.
The Saros, then, is just a nice round interval during which all these cycles repeat a whole number of times: 223 passes through the new moon is almost exactly equal to 242 laps in and out of the ecliptic, which is in turn almost exactly equal to 239 oscillations in the moon’s apparent size. If you saw a solar or lunar eclipse, just wait one Saros, and the same rough geometric arrangement of the celestial bodies will repeat.


On the left, a four-inch-wide clay cuneiform tablet from Babylon records lunar eclipses between 609 and 447 BCE. A fragment of an ancient Greek orrery known as the Antikythera mechanism appears on the right. Discovered in a shipwreck and dated to roughly the second century BCE, the orrery tracked cycles such as the Saros in order to predict eclipses and other astronomical events.
The Trustees of the British Museum (left); 2005 National Archaeological Museum in Athens
The moon’s orbit is actually more complicated than just these parameters, though. And regardless, this scheme doesn’t tell you where on Earth the resulting eclipse will be visible.
Halley and Beyond
By the time Halley read about the Saros and resuscitated it for his own use, many more centuries’ worth of multicultural effort had further refined the problem of eclipses, as the math historian Clemency Montelle described in the 2011 book Chasing Shadows. The Babylonians eventually moved past simple empirical rules like “wait one Saros” to more complicated numerical schemes that computed the moon’s future coordinates in the sky. The ancient Greeks melded their own geometric ideas about the cosmos with Babylonian-style numerical calculations. Building on top of that synthesis, Islamic-world astronomers such as al-Khwarizmi, the ninth-century namesake of the word “algorithm,” pulled in trigonometric functions and decimal numbers (from India) that they scribbled on the new medium of paper (from China) to develop still more advanced predictive methods, which were now echoing around Europe, too.
But Halley had something even newer to play with. Around the same time he fished the Saros out of antiquity, he also bankrolled the publication of his friend Isaac Newton’s ideas about gravitation, which Newton then applied to understanding the moon’s orbit. By 1715, with the first solar eclipse in many centuries approaching London, Halley’s predictive map was a mashup of ancient and modern ways of thinking.
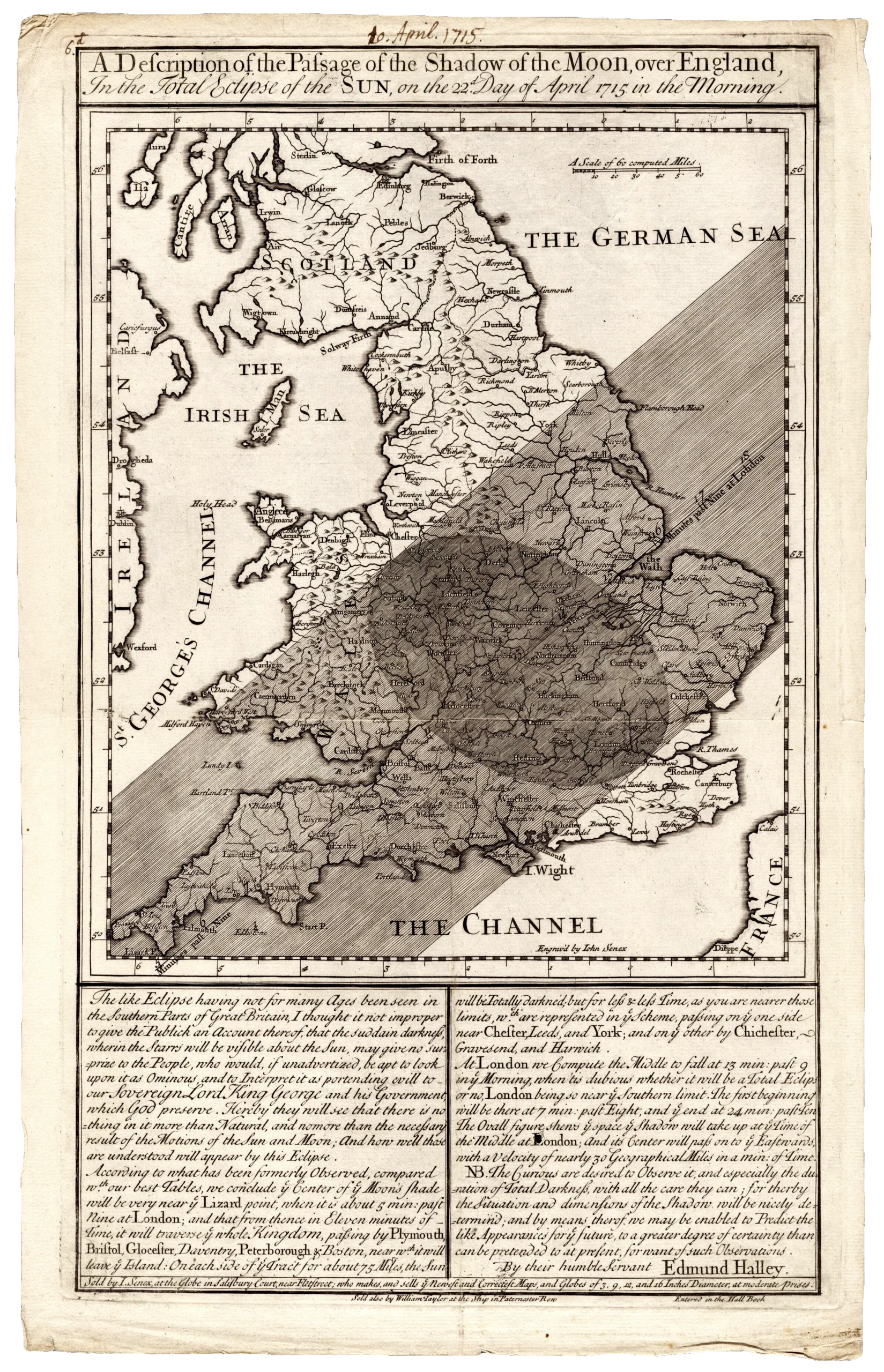
Days before the April 22, 1715, solar eclipse, the British astronomer Edmond Halley published this broadsheet predicting the timing and location of the event. His map predicting the path of totality turned out to be quite accurate — off by only about 20 miles on the northern edge.
Houghton Library, Harvard University
The next big step came in 1824, when the German astronomer Friedrich Bessel extended the Newtonian approach of thinking about eclipses using the laws of gravity. He envisioned the moon’s shadow cast onto an imaginary plane running through the center of the Earth. You could then project that shadow back up to the surface of the globe to see exactly where and when the shadow would strike, a process that eventually required thinking about the Earth as not a sphere but a lumpy, bumpy, spinning object. After Bessel, many nations had the global, imperial reach to chase down those shadows, said Deborah Kent, a math historian at the University of St. Andrews. By doing so, they could further refine their calculations in a battle for scientific soft-power supremacy.
Over the next century, eclipse expeditions helped settle one of the biggest mysteries in science: Was Mercury’s odd orbit due to an undiscovered sun-hugging planet (which would presumably become visible during an eclipse)? Or, as turned out to be the case, was there some problem with Newton’s understanding of gravity? These stakes made eclipse prediction and observation even more important, with scientists dispatched to all corners of the Earth with strict instructions on where exactly to be and which data to record. They then filed dry reports punctuated by the occasional “eruption of awe,” Kent said. “In almost every single one of them, there’s kind of two paragraphs of rhapsodic, Victorian, over-the-top description.”
In the 20th century, the problem transformed yet again. A proper prediction of eclipses always had to wrestle with the fact that the moon and everything else in the solar system are constantly tugging at each other. This wasn’t just the famously unsolvable “three-body problem”; it’s an N-body problem. When NASA began to launch people and robots toward solar system bodies, the need to know where these bodies were and where they would be in the future took on new urgency — and it became easier to figure out.
Because of mirrors left on the moon by the Apollo astronauts, we know where the moon is relative to Earth to within a couple of meters, according to Ryan Park, who leads the Solar System Dynamics group at NASA’s Jet Propulsion Laboratory. And with multiple spacecraft beaming back ranging data as they buzz around the solar system, we know the sun’s position with high accuracy, too. Park’s team feeds the lunar and solar position data — alongside similar parameters for the planets and hundreds of asteroids, and corrections for things like pressure from the solar wind, and not just the laws of Newton’s gravity but the subtler tweaks of general relativity — into a computer model. Then the model churns out a list of the predicted positions of everything, including the moon. And then, periodically, the JPL team updates their model and publishes new lists.
These positions, overkill for the task of predicting eclipses, are meant to be good enough for space travel. “I’m a little surprised,” said Park, when space mission developers ask about whether they’ll have to spend time figuring out where exactly the moon will be and how it moves. “I’m like, no, no, no, no, we solved the problem years ago.”




