Ideal Glass Would Explain Why Glass Exists at All

Miguel Ramos holds up a piece of fossilized amber. After settling for 110 million years, the amber was thought to approach the state of ideal glass, where molecules are packed together in the densest possible random arrangement.
James Rajotte for Quanta Magazine
Introduction
In 2008, Miguel Ramos read in the newspaper that 110-million-year-old amber bearing pristine Mesozoic insects had been discovered a few hours’ drive from Madrid, where he lived. A physicist who specializes in glass, Ramos had wanted for years to get his hands on ancient amber. He contacted the paleontologists working at the site, who invited him to visit.
“They provided me with the clear samples that are not good for them,” he said. “They have no interesting insects or whatever … but they are perfect for me.”
Ramos spent the next several years intermittently working on measurements of the ancient glass. He hoped that the fossilized tree resin, after aging for so long, might approach a hypothetical form of matter known as ideal glass.
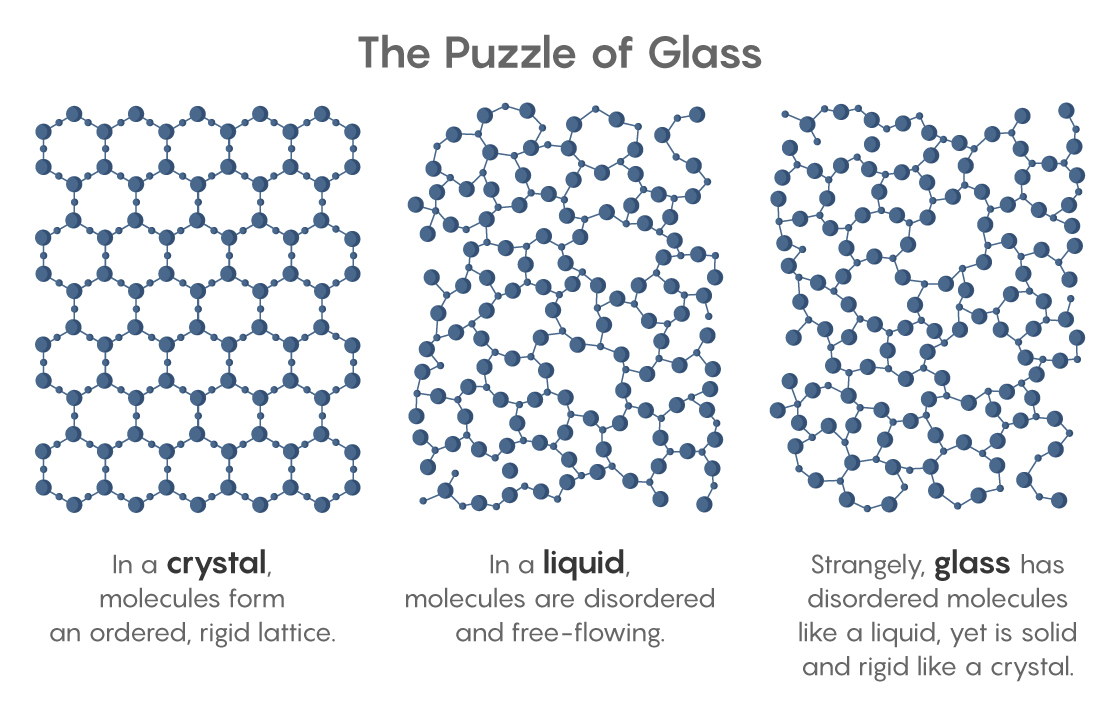
For decades, physicists have dreamed of this perfect amorphous solid. They desire ideal glass not so much for its own sake (though it would have unique, useful properties) but because its existence would solve a deep mystery. It’s the mystery posed by every window and mirror, every piece of plastic and hard candy, and even the cytoplasm that fills every cell. All of these materials are technically glass, for glass is anything that’s solid and rigid but made of disordered molecules like those in a liquid. Glass is a liquid in suspended animation, a liquid whose molecules curiously cannot flow. Ideal glass, if it exists, would tell us why.
Inconveniently, ideal glass would take so long to form that it may not have done so in all of cosmic history. Physicists can only seek indirect evidence that, given unlimited time, it would. Ramos, an experimental physicist at the Autonomous University of Madrid, hoped that after 110 million years of aging, the Spanish amber might have started to show glimmers of perfection. If so, he would know what the molecules in ordinary glass are really doing when they appear to do nothing.
Ramos’s amber measurements are part of a surge of interest in ideal glass. In the past few years, new methods of making glass and simulating it on computers have led to unexpected progress. Major clues have emerged about the nature of ideal glass and its connection to ordinary glass. “These studies provide renewed support for the hypothesis of the existence of an ideal-glass state,” said Ludovic Berthier, a physicist at the University of Montpellier who was centrally involved in the recent computer simulations.
But the emerging picture of ideal glass only makes sense if we set aside one piece of evidence.
“Indeed,” Berthier said, “the amber work stands out as difficult to rationalize.”
The Paradox of Glass
When you cool a liquid, it will either crystallize or harden into glass. Which of the two happens depends on the substance and on the subtleties of the process that glassblowers have learned through trial and error over thousands of years. “Avoiding crystallization is a dark art,” said Paddy Royall, a glass physicist at the University of Bristol in the United Kingdom.
The two options differ greatly.
Crystallization is a dramatic switch from the liquid phase, in which molecules are disordered and free flowing, to the crystal phase, in which molecules are locked in a regular, repeating pattern. Water freezes into ice at zero degrees Celsius, for instance, because the H2O molecules stop jiggling around just enough at that temperature to feel each other’s forces and fall into lockstep.
Other liquids, when cooled, more easily become glass. Silica, for example — window glass — starts as a molten liquid well above 1,000 degrees Celsius; as it cools, its disordered molecules contract slightly, crowding a bit closer together, which makes the liquid increasingly viscous. Eventually, the molecules stop moving altogether. In this gradual glass transition, the molecules don’t reorganize. They simply grind to a halt.
Lucy Reading-Ikkanda/Quanta Magazine
Exactly why the cooling liquid hardens remains unknown. If the molecules in glass were simply too cold to flow, it should still be possible to squish them into new arrangements. But glass doesn’t squish; its jumbled molecules are truly rigid, despite looking the same as molecules in a liquid. “Liquid and glass have the same structure, but behave differently,” said Camille Scalliet, a glass theorist at the University of Cambridge. “Understanding that is the main question.”
A clue came in 1948, when a young chemist named Walter Kauzmann noticed what became known as the entropy crisis, a glassy paradox that later researchers realized ideal glass could resolve.
Kauzmann knew that the more slowly you cool a liquid, the more you can cool it before it transitions into glass. And slower-formed glass ends up denser and more stable, because its molecules had longer to shuffle around (while the liquid was still viscous) and find tighter, lower-energy arrangements. Measurements indicated a corresponding reduction in the entropy, or disorder, of the slower-formed glass — fewer ways its molecules could be arranged with the same low energy.
Extrapolating the trend, Kauzmann realized that if you could cool a liquid slowly enough, you could cool it all the way down to a temperature now known as the Kauzmann temperature before it fully hardened. At that temperature, the resulting glass would have an entropy as low as that of a crystal. But crystals are neat, orderly structures. How could glass, disordered by definition, possess equal order?
No ordinary glass could, which implied that something special must happen at the Kauzmann temperature. Crisis would be avoided if a liquid, upon reaching that temperature, attained the ideal-glass state — the densest possible random packing of molecules. Such a state would exhibit “long-range amorphous order,” where each molecule feels and affects the position of every other, so that in order to move, they must move as one. The hidden long-range order of this putative state could rival the more obvious orderliness of a crystal. “That observation right there was at the heart of why people thought there should be an ideal glass,” said Mark Ediger, a chemical physicist at the University of Wisconsin, Madison.
According to this theory, first advanced by Julian Gibbs and Edmund DiMarzio in 1958, ideal glass is a true phase of matter, akin to the liquid and crystal phases. The transition to this phase just takes too long, requiring too slow a cooling process, for scientists to ever see. The ideal-glass transition is “masked,” said Daniel Stein, a condensed matter physicist at New York University, by the liquid becoming “so viscous that everything is arrested.”
“It’s sort of like looking through a glass darkly,” Stein said. “We can’t get to [ideal glass] or see it. But we can theoretically try to create accurate models of what’s going on there.”
A New Glass
Unexpected help has come from experiments. There was never any hope of forming ideal glass by cooling a liquid, the glassmaking method humans have used for millennia. You’d have to cool a liquid impossibly slowly — perhaps even infinitely slowly — to keep it from hardening before it hit the Kauzmann temperature. But in 2007, Ediger, the Wisconsin physicist, developed a new method of glassmaking. “We figured out there was another way to make glasses that are high density and close to the ideal-glass state by a completely different route,” he said.
Ediger and his team discovered that they could create “ultra-stable glasses” that exist in a state somewhere between ordinary and ideal. Using a method called vapor deposition, they dropped molecules one by one onto a surface as if they were playing Tetris, allowing each molecule to settle into its snuggest fit in the forming glass before the next molecule came down. The resulting glass was denser, more stable, and lower in entropy than all of the glasses throughout human history. “These materials have the properties that you would expect if you took a liquid and cooled it over the course of a million years,” Ediger said.
Another property of ultra-stable glass would eventually reveal the most promising road map to ideal glass.
Two groups, one of them led by Miguel Ramos in Madrid, identified that property in 2014, when they found that ultra-stable glass departs from a universal characteristic of all ordinary glass.
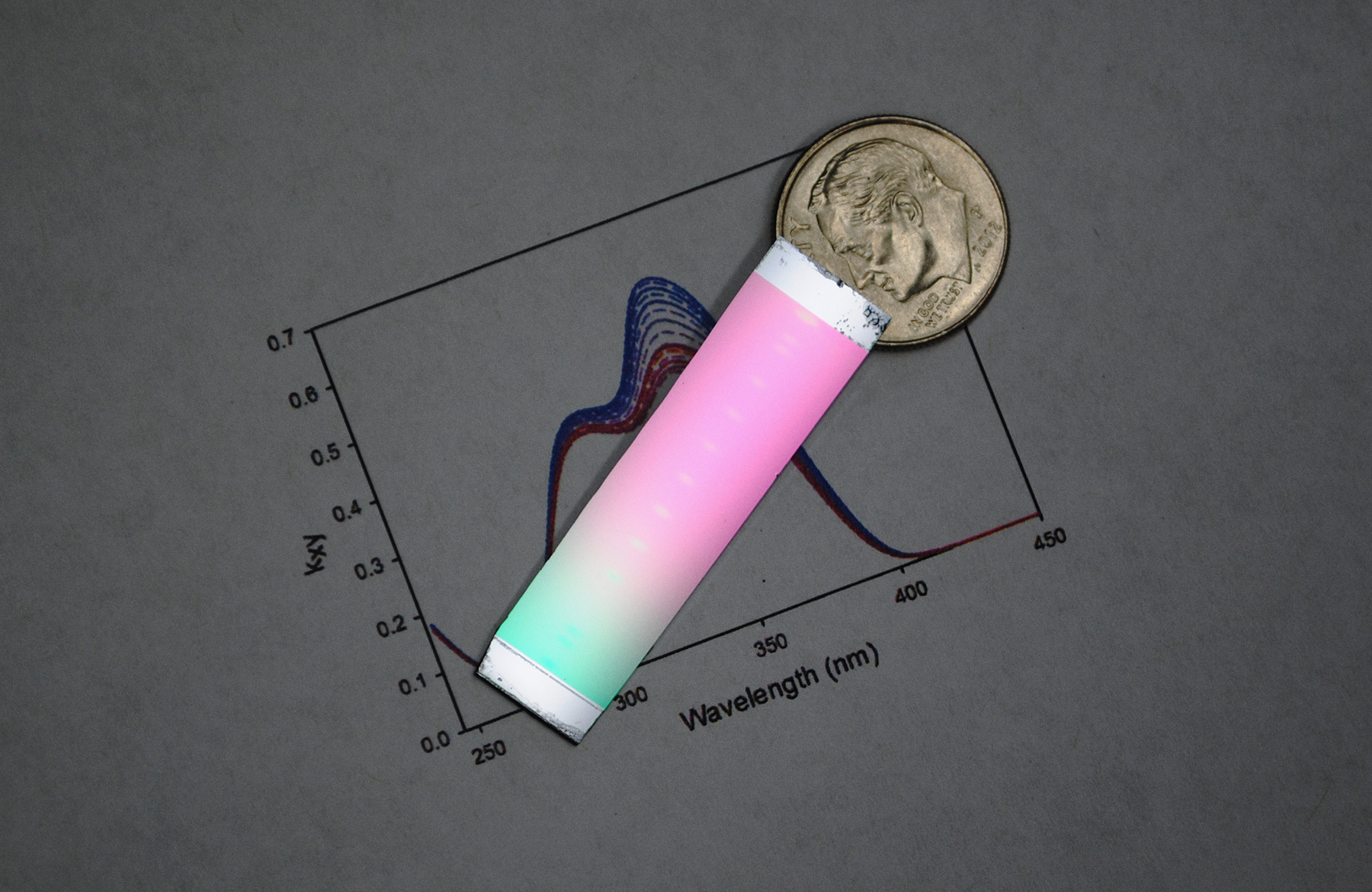
Vapor-deposited glass can have different properties depending on the temperature at which it is created. In this sample, researchers maintained a temperature gradient across the sample, which led to the rainbow effect. The ultrastable glass is toward the middle of the sample.
Diane Walters, University of Wisconsin-Madison
Physicists have known for decades that ultra-cold glass has a high heat capacity — the amount of heat needed to raise its temperature. Glass can take way more heat than a crystal can near absolute zero, with a heat capacity that’s directly proportional to the temperature.
Theorists including Phil Anderson, the revered Nobel Prize-winning condensed matter physicist, suggested an explanation in the early 1970s. They argued that glass contains many “two-level systems,” little clusters of atoms or molecules that can slip back and forth between two alternative, equally stable configurations. “You can imagine a whole bunch of atoms kind of shifting from one configuration to a very slightly different configuration,” said Frances Hellman of the University of California, Berkeley, “which just doesn’t exist in a crystalline material.”
Although the atoms or molecules are too boxed in by their neighbors to do much switching on their own, at room temperature, heat activates the two-level systems, providing the atoms with the energy they need to shuffle around. This activity diminishes as the glass’s temperature drops. But near absolute zero, quantum effects become important: Groups of atoms in the glass can quantum mechanically “tunnel” between the alternative configurations, passing right through any obstacles, and even occupy both levels of the two-level system at once. The tunneling absorbs a lot of heat, producing glass’s characteristic high heat capacity.
Several years after Ediger figured out how to make ultra-stable glass, Hellman’s group at Berkeley and Ramos’ in Madrid independently set out to study whether it might depart from that universal heat capacity near absolute zero. In their respective experiments, they probed the low-temperature properties of ultra-stable silicon and ultra-stable indomethacin (a chemical that’s also used as an anti-inflammatory drug). Sure enough, they found that both glasses had far lower heat capacity than usual near absolute zero, in line with a crystal’s. This suggested that ultra-stable glass has fewer two-level systems to tunnel between. The molecules are in especially snug configurations with few competitors.

Ramos cools amber down to temperatures close to absolute zero to test how closely it approaches the state of ideal glass.
James Rajotte for Quanta Magazine
If ultra-stable glass’s exceptionally low heat capacity really does come from having fewer two-level systems, then ideal glass naturally corresponds to the state with no two-level systems at all. “It’s just perfectly, somehow, positioned where all the atoms are disordered — it doesn’t have a crystal structure — but there’s nothing moving at all,” said David Reichman, a theorist at Columbia University.
Furthermore, the drive toward this state of perfect long-range amorphous order, where each molecule affects the positions of all others, could be what causes liquids to harden into the glass we see (and see through) all around us.
In this emerging picture, when a liquid becomes a glass, it’s actually attempting to transition to the ideal-glass phase, drawn by a fundamental pull toward long-range order. The ideal glass is the endpoint, Royall said, but as the molecules try to crowd closer together, they get stuck; the increasing viscosity prevents the system from ever reaching the desired state.
Recently, groundbreaking computer simulations were used to test these ideas. Simulating ultra-stable glass on a computer used to be infeasible because of the extraordinary computing time required for the simulated molecules to crowd together. Two years ago, though, Berthier found a trick that allowed him to speed up the process by a factor of 1 trillion. His algorithm picks two particles at random and swaps their positions. These shake-ups help the simulated liquid stay unstuck, allowing molecules to settle into snugger fits — just as the ability to swap two ill-fitting shapes would help in Tetris.
In a paper that’s under review for publication in Physical Review Letters, Berthier, Scalliet, Reichman and two co-authors reported that the more stable the simulated glass, the fewer two-level systems it has. As with Hellman’s and Ramos’ heat capacity measurements, the computer simulations suggest that two-level systems — competing configurations of groups of molecules — are the source of glass’s entropy. The fewer of these alternative states there are, the more stability and long-range order an amorphous solid has, and the closer it is to ideal.
The theorists Vassiliy Lubchenko of the University of Houston and Peter Wolynes of Rice University suggested back in 2007 that ideal glass should have no two-level systems. “I’m quite happy with Berthier’s result,” Wolynes said by email.
The Amber Anomaly
But then there’s that amber.
Ramos and his collaborators published their comparisons of old and “rejuvenated” samples of the yellow glass in Physical Review Letters in 2014. They found that the 110-million-year-old amber had grown about 2% denser, in line with ultra-stable glass. This should suggest that the amber had indeed stabilized over time, as little groups of molecules slipped, one by one, into lower-energy arrangements.
But when the Madrid team cooled the ancient glass nearly to absolute zero and measured its heat capacity, the results told a different story. The aged amber had the same high heat capacity as new amber — and all other ordinary glass. Its molecules seemed to be tunneling between just as many two-level systems as usual.
Why didn’t the number of two-level systems drop over time as the amber stabilized and became denser? The findings don’t fit.
“I really like the experiments on amber, but making an amber glass is sort of a messy process,” said Ediger, the originator of the vapor-deposition method. “It’s basically tree sap that over time chemically changes and solidifies as well as ages.” He thinks impurities in the Spanish amber might have sullied the heat capacity measurements.
Researchers plan to do further experiments on amber, as well as lab-made and simulated glass, hoping to uncover more details of two-level systems and to get closer to the putative ideal state. Reichman noted that it may never be possible to prove its existence with complete certainty. “Maybe one day we will know, at least on the computer, how to precisely pack particles in a way that would be the ideal glass we are looking for,” he said. “But we would then have to wait a very long time — too long — to see if it remains stable.”
Editor’s Note: Ludovic Berthier and David Reichman have received funding from the Simons Foundation, which also supports this editorially independent publication. Simons Foundation funding plays no role in our coverage.
This article was reprinted on Wired.com.



