Mathematicians Catch a Pattern by Figuring Out How to Avoid It

Mathematicians are making inroads in the grand effort to find structure in random-seeming sets of numbers.
Celia Lowenthal for Quanta Magazine
Introduction
Some mathematical patterns are so subtle you could search for a lifetime and never find them. Others are so common that they seem impossible to avoid.
A new proof by Sarah Peluse of the University of Oxford establishes that one particularly important type of numerical sequence is, ultimately, unavoidable: It’s guaranteed to show up in every single sufficiently large collection of numbers, regardless of how the numbers are chosen.
“There’s a sort of indestructibility to these patterns,” said Terence Tao of the University of California, Los Angeles.
Peluse’s proof concerns sequences of numbers called “polynomial progressions.” They are easy to generate — you could create one yourself in short order — and they touch on the interplay between addition and multiplication among the numbers.
For several decades, mathematicians have known that when a collection, or set, of numbers is small (meaning it contains relatively few numbers), the set might not contain any polynomial progressions. They also knew that as a set grows it eventually crosses a threshold, after which it has so many numbers that one of these patterns has to be there, somewhere. It’s like a bowl of alphabet soup — the more letters you have, the more likely it is that the bowl will contain words.
But prior to Peluse’s work, mathematicians didn’t know what that critical threshold was. Her proof provides an answer — a precise formula for determining how big a set needs to be in order to guarantee that it contains certain polynomial progressions.
Previously, mathematicians had only a vague understanding that polynomial progressions are embedded among the whole numbers (1, 2, 3 and so on). Now they know exactly how to find them.
Finding Patterns
To get a sense of these patterns, consider one that is slightly simpler than the polynomial progressions Peluse worked with. Start with 2 and keep adding 3: 2, 5, 8, 11, 14, and so on. This pattern — where you begin with one number and keep adding another — is called an “arithmetic progression.” It’s one of the most studied, and most prevalent, patterns in math.

There are two main facts to understand about the frequency with which arithmetic progressions appear among the whole numbers.
In 1975, Endre Szemerédi proved one of them. First, he said, decide how long you want your arithmetic progression to be. It could be any such pattern with four terms (2, 5, 8, 11), or seven terms (14, 17, 20, 23, 26, 29, 32), or any number of terms you want. Then he proved that once a set reaches some exact size (which he couldn’t identify), it must contain an arithmetic pattern of that length. In doing so, he codified the intuition that among a large enough collection of numbers there has to be a pattern somewhere.
“Szemerédi basically said that complete disorder is impossible. No matter what set you take, there have to be little inroads of structure inside of it,” said Ben Green of Oxford.
But Szemerédi’s theorem didn’t say anything about how big a collection of numbers needs to be before these patterns become inevitable. He simply said that there exists a set of numbers, of some unknown size, that contains an arithmetic pattern of the length you’re looking for.
More than two decades later, a mathematician put a number on that size — in effect, proving the second main fact about these arithmetic patterns.
In 2001, Timothy Gowers of the University of Cambridge proved that if you want to be guaranteed to find, say, a five-term arithmetic progression, you need a set of numbers that’s at least some exact size — and he identified just what that size is. (Actually stating the size is complicated, as it involves enormous exponential numbers.)
To understand what Gowers did, you have to understand what mathematicians mean when they talk about the “size” of a set of numbers and the idea of “big enough.”
First, choose an interval on the number line, say 1 to 1,000, or something more random like 17 to 1,016. The endpoints of the interval don’t matter — only the length does. Next, determine the proportion of the numbers within that interval that you’re going to put into your set. For example, if you create a set with 100 numbers from 1 to 1,000, the size of your set is 10% of the interval.
Gowers’ proof works regardless of how you choose the numbers in that set. You could take the first 100 odd numbers between 1 and 1,000, the first 100 numbers that end in a 6, or even 100 random numbers. Whatever your method, Gowers proved that once a set takes up enough space (not necessarily 10%) in a long enough interval, it can’t help but include a five-term arithmetic progression. And he did the same for arithmetic progressions of any length you want.
“After Gowers, you know that if you give me an arithmetic progression of any length, then any subset” of numbers of some specified size must necessarily contain that progression, Peluse said.
Peluse’s work parallels Gowers’ achievement, except that she focused on polynomial progressions instead.
In an arithmetic progression, remember, you choose one starting number and keep adding another. In the type of polynomial progressions studied by Peluse, you still pick a starting value, but now you add powers of another number. For example: 2, 2 + 31, 2 + 32, 2 + 33, 2 + 34. Or 2, 5, 11, 29, 83. (Her progressions also had only one term for each power, a requirement that makes them more manageable.)
These polynomial progressions are closely related to an important type of pattern known as a geometric progression, formed by raising a number to increasingly high powers: 31, 32, 33, 34. These appear naturally in many areas of math and physics, and they’ve fascinated mathematicians for millennia. Geometric progressions are rare among even large sets of numbers, but if you tweak a geometric progression slightly — by adding a constant, like 2, to each term — you get a polynomial progression. And these seem to be everywhere.
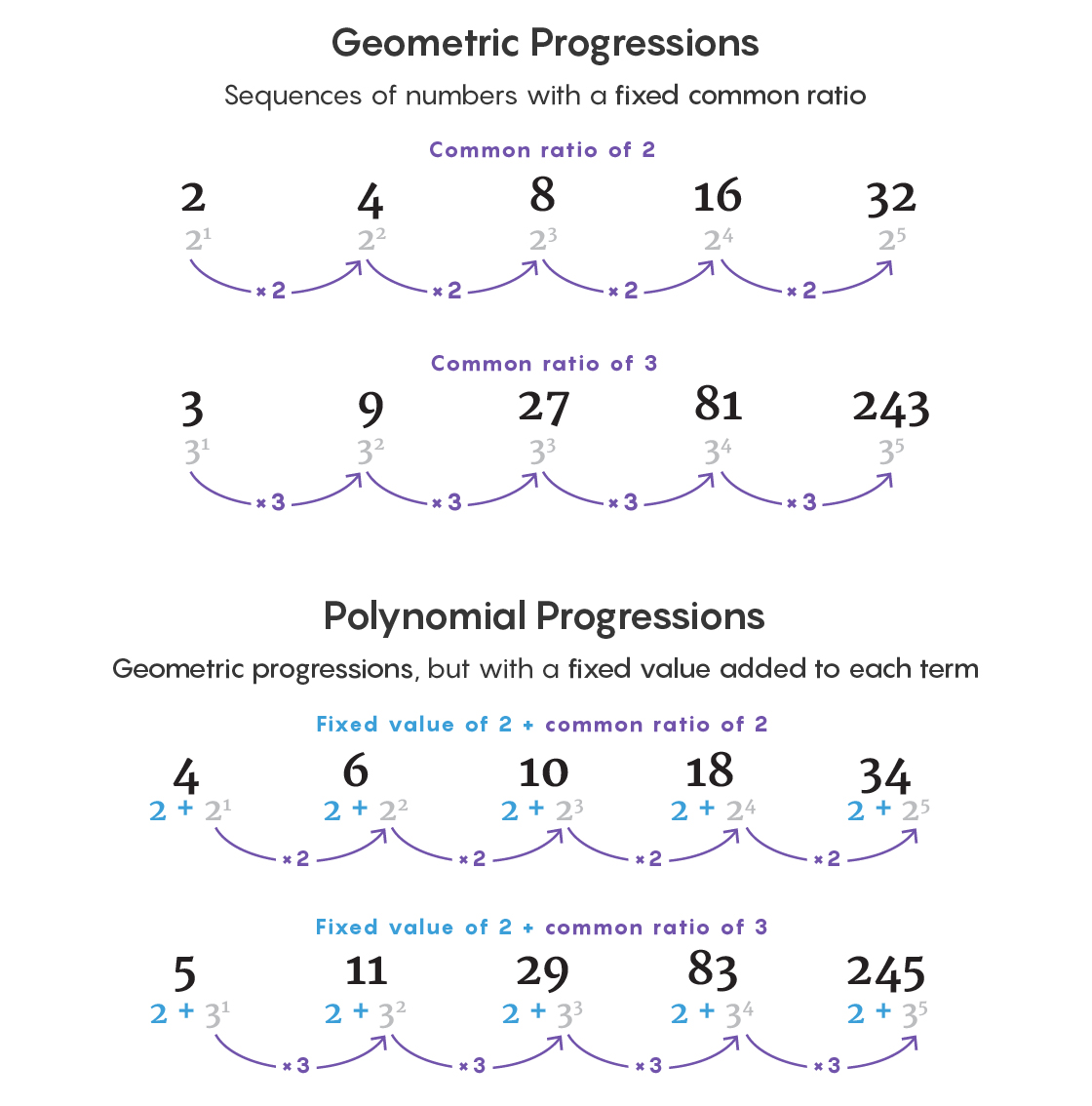
“You can construct large sets of [numbers] that don’t contain geometric progressions. But if you allow yourself more freedom and shift your geometric progression,” creating a polynomial progression, then large sets seem to be forced to contain them, said Sean Prendiville of Lancaster University, who has collaborated with Peluse on polynomial progressions.
In 1996, Vitaly Bergelson and Alexander Leibman proved that once a set of numbers gets big enough, it has to contain polynomial progressions — the polynomial equivalent of Szemerédi’s work. But once again, that left mathematicians with no idea what “big enough” meant.
Peluse answered that question in a counterintuitive way — by thinking about exactly what it would take for a set of numbers not to contain the pattern you’re looking for.
Fighting Patterns With Patterns
Peluse wanted to determine how big a set needs to be — what percentage of the numbers in an interval it needs to include — in order to ensure that it contains a given polynomial progression. To do that, she had to think about all the ways a set of numbers could avoid containing the progression — and then to prove that past a certain size, even the cleverest avoidance strategies no longer work.
You can think about the problem as a challenge. Imagine that someone asks you to create a set containing half the numbers between 1 and 1,000. You win if the set doesn’t contain the first four terms of a polynomial progression. How would you select the numbers?
Your instinct might be to choose the numbers at random. That instinct is wrong.
“Most sets are in the middle of the bell curve. The number of polynomial progressions they contain is the average number,” Prendiville said. And that average is way more than the zero you want.
It’s similar to how, if you chose a person at random from the world’s population, you’d probably get someone close to average height. If your goal was to find a much rarer 7-footer, you’d need to search in a more targeted way.
So to win the number-picking challenge, you’ll need a more organized way of deciding which ones to include in your set of 500. You might notice, for example, that if you choose only even numbers, you eliminate the possibility that your set contains polynomial progressions with any odd numbers. Progress! Of course, you’ve also increased the likelihood that your set contains polynomial progressions made up of even numbers.
But the point is that by coming up with a structured way of choosing those 500 numbers, you can rule out the possibility that your set will contain certain polynomial progressions. In other words, it takes a pattern to avoid a pattern.
Peluse set out to prove that after reaching a certain size, even the most cleverly constructed sets still have to contain a given polynomial progression. Essentially, she wanted to identify the critical point at which every time you avoid one instance of a polynomial progression, you back into another, as with the odd and even numbers.
To do that, she had to find a way to quantify just how much structure a set contains.
Measuring Structure
Before Peluse’s paper, many mathematicians had tried to understand when polynomial progressions appear among sets of numbers. The researchers included some of the most accomplished minds in the field, but none of them made significant progress toward figuring out how big a set needs to be in order to contain polynomial progressions of different lengths.
The main impediment was that mathematicians had no idea how to capture, in a precise way, the kinds of structures that might allow a set to avoid containing polynomial progressions. There was one candidate technique. But at the time Peluse started her work, it was completely inapplicable to questions about polynomial progressions.
The technique originated in Gowers’ 2001 work on arithmetic progressions. There, Gowers had created a test, called the “Gowers norm,” which detects specific kinds of structures in a set of numbers. The test generates a single number quantifying the amount of structure in the set — or, to put it differently, it quantifies how far the set is from being a set of random numbers.
“The notion of looking random is not a well-defined mathematical notion,” Green said. Gowers found a way to quantify what this should mean.
A set can be structured to a greater or lesser extent. Sets containing random numbers have no structure at all — and therefore are likely to contain numerical patterns. They have a lower Gowers norm. Sets containing only odd numbers, or only multiples of 10, have a rudimentary structure. It’s easy to prove that past a certain size, sets with these kinds of simple designs also contain different kinds of patterns.
The most difficult sets to work on are those with a very intricate structure. These sets could still look random when in fact they’re constructed according to some kind of very subtle rule. They have a high Gowers norm, and they present the best chance of systematically avoiding patterns as the sets themselves grow larger.
While Gowers used these techniques to answer questions about arithmetic progressions, they were not applicable to questions about polynomial progressions. This is because arithmetic progressions are evenly spaced, while the terms in polynomial progressions jump wildly from one to the next. The Gowers norms were useful for studying polynomial progressions the way a weed whacker is good for stripping paint from a house: the right general idea, even if it’s not suited to the job.
In her new proof, Peluse used the basic idea of the Gowers norm to create a wholly new way of analyzing the kinds of structures relevant to polynomial progressions. She used this technique, called “degree-lowering,” to prove that for the polynomial progressions she was interested in, the only kinds of structures you actually need to worry about are the blunt, simple ones with a low Gowers norm. That’s because polynomial progressions veer so extremely from one term to the next that they inevitably run through subtler numerical obstacles — like a bull crashing through display tables on its way out of a china shop.
Peluse’s formula is complicated to state. It involves taking a double logarithm of the length of the initial interval from which you choose the numbers in your set. The minimum size she came up with is also not necessarily the true minimum size — future work might find that the critical threshold is even lower. But before her proof, mathematicians had no quantitative understanding at all about when polynomial progressions were guaranteed.
“She’s the first person to show how large sets need to be,” Prendiville said.
Peluse’s proof answers one quantitative question about polynomial progressions. Mathematicians now hope they can use it to answer another — about when polynomial progressions appear in sets composed entirely of prime numbers, which are the most important numbers in mathematics and notoriously resistant to patterns. Before Peluse’s proof, mathematicians had no idea how to approach that question.
“There’s a hope you can import some of the arguments from my paper into the primes setting,” Peluse said.