Matrix Multiplication Inches Closer to Mythic Goal
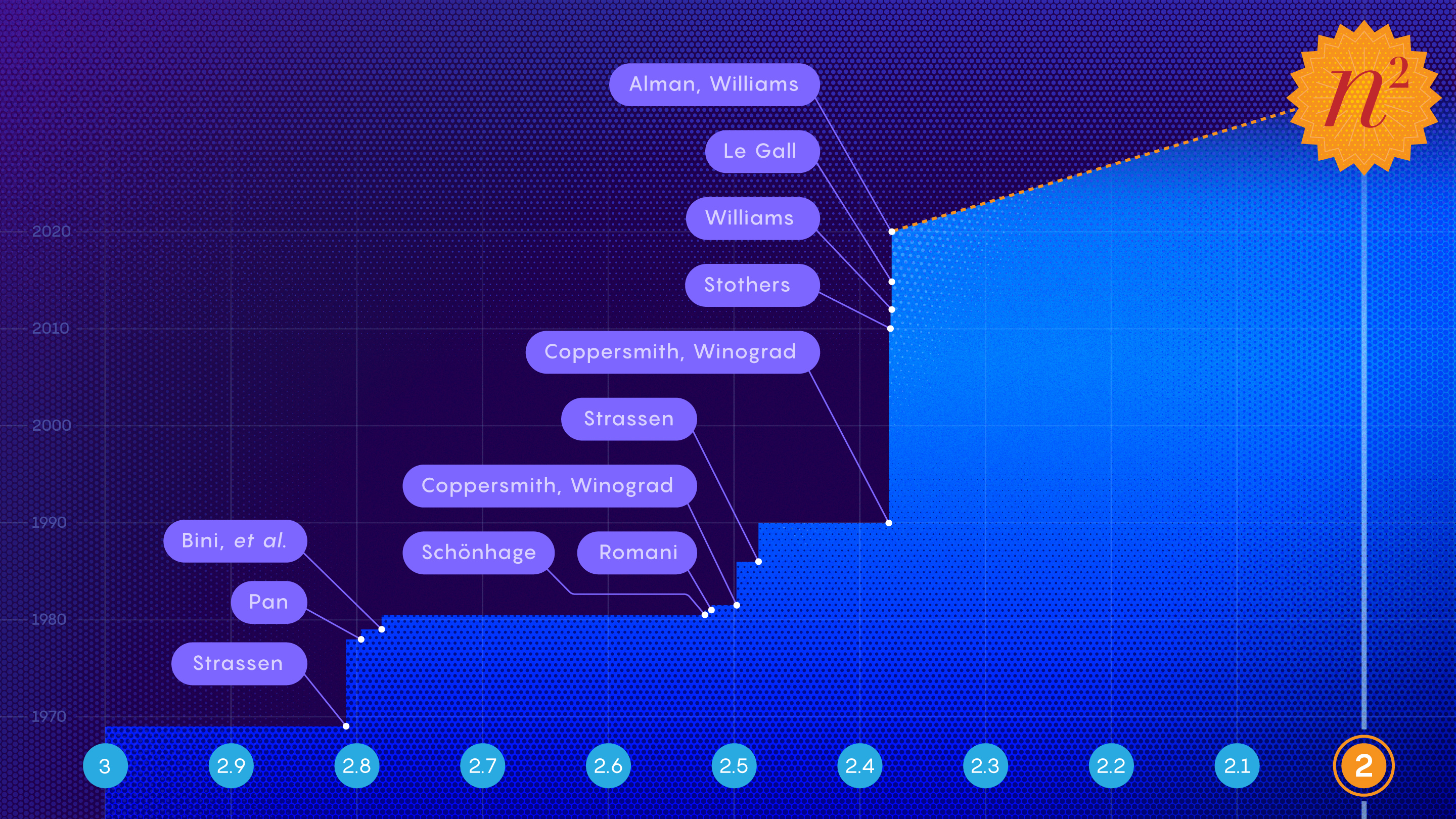
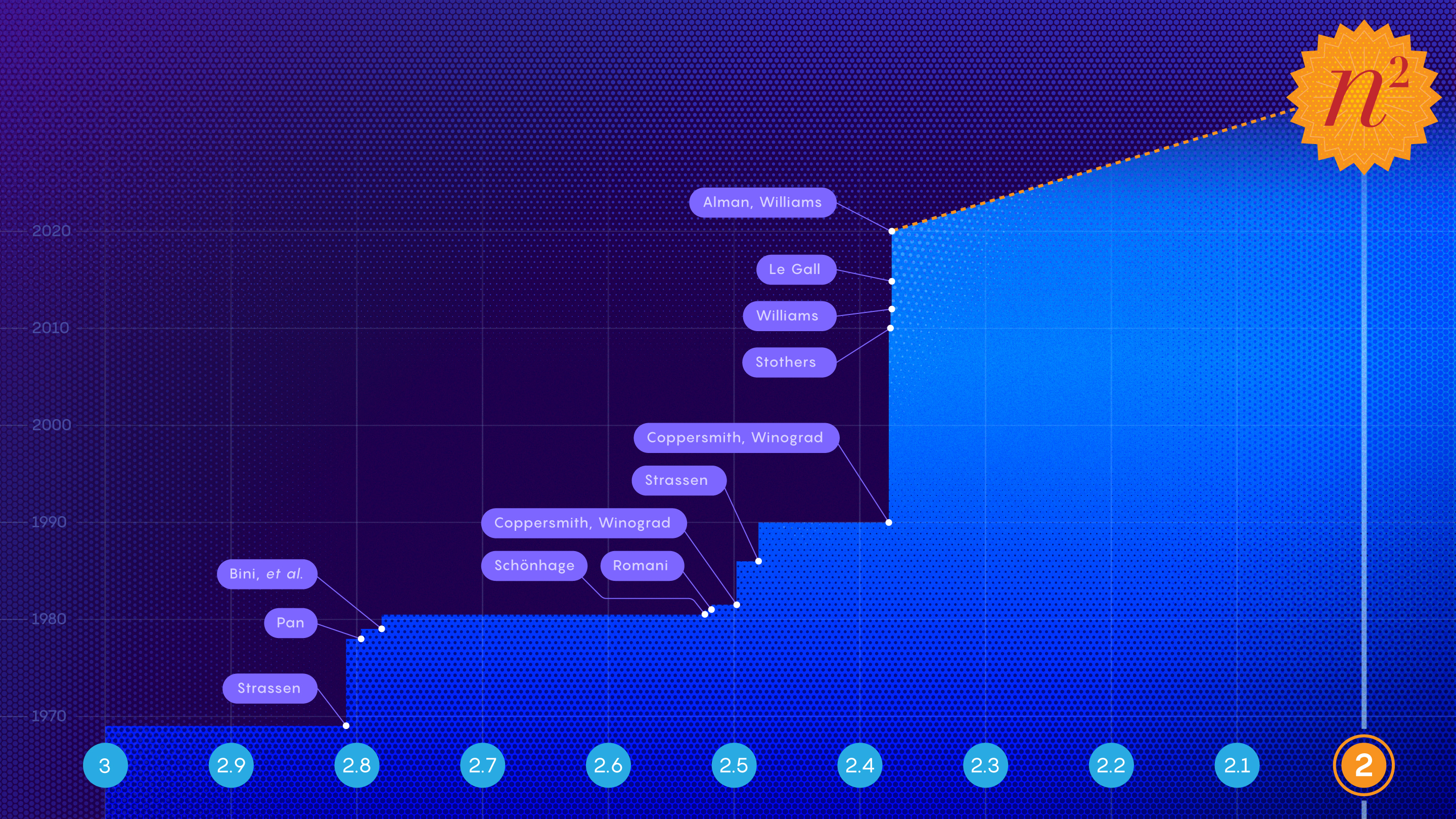
Mathematicians have been getting closer to their goal of reaching exponent two — meaning multiplying a pair of n-by-n matrices in only n2 steps — but will they ever reach it?
Samuel Velasco/Quanta Magazine; source: Jochen Burghardt
Introduction
For computer scientists and mathematicians, opinions about “exponent two” boil down to a sense of how the world should be.
“It’s hard to distinguish scientific thinking from wishful thinking,” said Chris Umans of the California Institute of Technology. “I want the exponent to be two because it’s beautiful.”
“Exponent two” refers to the ideal speed — in terms of number of steps required — of performing one of the most fundamental operations in math: matrix multiplication. If exponent two is achievable, then it’s possible to carry out matrix multiplication as fast as physically possible. If it’s not, then we’re stuck in a world misfit to our dreams.
Matrices are arrays of numbers. When you have two matrices of compatible sizes, it’s possible to multiply them to produce a third matrix. For example, if you start with a pair of two-by-two matrices, their product will also be a two-by-two matrix, containing four entries. More generally, the product of a pair of n-by-n matrices is another n-by-n matrix with n2 entries.
For this reason, the fastest one could possibly hope to multiply pairs of matrices is in n2 steps — that is, in the number of steps it takes merely to write down the answer. This is where “exponent two” comes from.
And while no one knows for sure whether it can be reached, researchers continue to make progress in that direction.
A paper posted in October comes the closest yet, describing the fastest-ever method for multiplying two matrices together. The result, by Josh Alman, a postdoctoral researcher at Harvard University, and Virginia Vassilevska Williams of the Massachusetts Institute of Technology, shaves about one-hundred-thousandth off the exponent of the previous best mark. It’s typical of the recent painstaking gains in the field.
To get a sense for this process, and how it can be improved, let’s start with a pair of two-by-two matrices, A and B. When computing each entry of their product, you use the corresponding row of A and corresponding column of B. So to get the top-right entry, multiply the first number in the first row of A by the first number in the second column of B, then multiply the second number in the first row of A by the second number in the second column of B, and add those two products together.
Samuel Velasco/Quanta Magazine
This operation is known as taking the “inner product” of a row with a column. To compute the other entries in the product matrix, repeat the procedure with the corresponding rows and columns.
Altogether, the textbook method for multiplying two-by-two matrices requires eight multiplications, plus some additions. Generally, this way of multiplying two n-by-n matrices together requires n3 multiplications along the way.
As matrices grow larger, the number of multiplications needed to find their product increases much faster than the number of additions. While it takes eight intermediate multiplications to find the product of two-by-two matrices, it takes 64 to find the product of four-by-four matrices. However, the number of additions required to add those sets of matrices is much closer together. Generally, the number of additions is equal to the number of entries in the matrix, so four for the two-by-two matrices and 16 for the four-by-four matrices. This difference between addition and multiplication begins to get at why researchers measure the speed of matrix multiplication purely in terms of the number of multiplications required.
“Multiplications are everything,” said Umans. “The exponent on the eventual running time is fully dependent only on the number of multiplications. The additions sort of disappear.”
For centuries people thought n3 was simply the fastest that matrix multiplication could be done. In 1969, Volker Strassen reportedly set out to prove that there was no way to multiply two-by-two matrices using fewer than eight multiplications. Apparently he couldn’t find the proof, and after a while he realized why: There’s actually a way to do it with seven!
Strassen came up with a complicated set of relationships that made it possible to replace one of those eight multiplications with 14 extra additions. That might not seem like much of a difference, but it pays off thanks to the importance of multiplication over addition. And by finding a way to save a single multiplication for small two-by-two matrices, Strassen found an opening that he could exploit when multiplying larger matrices.
“This tiny improvement leads to huge improvements with big matrices,” Vassilevska Williams said.


Virginia Vassilevska Williams of the Massachusetts Institute of Technology and Josh Alman of Harvard University discovered the fastest-ever way to multiply two matrices, clocking in at n2.3728596 steps.
Jared Charney; Richard TK Hawke
Say, for example, you want to multiply a pair of eight-by-eight matrices. One way to do it is to break each big matrix into four four-by-four matrices, so each one has four entries. Because a matrix can also have entries that are themselves matrices, you can thus think of the original matrices as a pair of two-by-two matrices, each of whose four entries is itself a four-by-four matrix. Through some manipulation, these four-by-four matrices can themselves each be broken into four two-by-two matrices.
The point of this reduction — of repeatedly breaking bigger matrices into smaller matrices — is that it’s possible to apply Strassen’s algorithm over and over again to the smaller matrices, reaping the savings of his method at each step. Altogether, Strassen’s algorithm improved the speed of matrix multiplication from n3 to n2.81 multiplicative steps.
The next big improvement took place in the late 1970s, with a fundamentally new way to approach the problem. It involves translating matrix multiplication into a different computational problem in linear algebra involving objects called tensors. The particular tensors used in this problem are three-dimensional arrays of numbers composed of many different parts, each of which looks like a small matrix multiplication problem.
Matrix multiplication and this problem involving tensors are equivalent to each other in a sense, yet researchers already had faster procedures for solving the latter one. This left them with the task of determining the exchange rate between the two: How big are the matrices you can multiply for the same computational cost that it takes to solve the tensor problem?
“This is a very common paradigm in theoretical computer science, of reducing between problems to show they’re as easy or as hard as each other,” Alman said.
In 1981 Arnold Schönhage used this approach to prove that it’s possible to perform matrix multiplication in n2.522 steps. Strassen later called this approach the “laser method.”
Over the last few decades, every improvement in matrix multiplication has come from improvements in the laser method, as researchers have found increasingly efficient ways to translate between the two problems. In their new proof, Alman and Vassilevska Williams reduce the friction between the two problems and show that it’s possible to “buy” more matrix multiplication than previously realized for solving a tensor problem of a given size.
“Josh and Virginia have basically found a way of taking the machinery inside the laser method and tweaking it to get even better results,” said Henry Cohn of Microsoft Research.
The paper improves the theoretical speed limit on matrix multiplication to n2.3728596.
It also allows Vassilevska Williams to regain the matrix multiplication crown, which she previously held in 2012 (n2.372873), then lost in 2014 to François Le Gall (n2.3728639).
Yet for all the jockeying, it’s also clear this approach is providing diminishing returns. In fact, Alman and Vassilevska Williams’s improvement may have nearly maxed out the laser method — remaining far short of that ultimate theoretical goal.
“There isn’t likely to be a leap to exponent two using this particular family of methods,” Umans said.
Getting there will require discovering new methods and sustaining the belief that it’s even possible.
Vassilevska Williams remembers a conversation she once had with Strassen about this: “I asked him if he thinks you can get [exponent 2] for matrix multiplication and he said, ‘no, no, no, no, no.’”



