Mathematicians Marvel at ‘Crazy’ Cuts Through Four Dimensions

Kristina Armitage/Quanta Magazine
Introduction
The central objects of study in topology are spaces called manifolds, which look flat when you zoom in on them. The surface of a sphere, for instance, is a two-dimensional manifold. Topologists understand such two-dimensional manifolds very well. And they have developed tools that let them make sense of three-dimensional manifolds and those with five or more dimensions.
But in four dimensions, “everything goes a bit crazy,” said Sam Hughes, a postdoctoral researcher at the University of Oxford. Tools stop working; exotic behavior emerges. As Tom Mrowka of the Massachusetts Institute of Technology explained, “There’s just enough room to have interesting phenomena, but not so much room that they fall apart.”
In the early 1990s, Mrowka and Peter Kronheimer of Harvard University were studying how two-dimensional surfaces can be embedded within four-dimensional manifolds. They developed new techniques to characterize these surfaces, allowing them to gain crucial insights into the otherwise inaccessible structure of four-dimensional manifolds. Their findings suggested that the members of a broad class of surfaces all slice through their parent manifold in a relatively simple way, leaving a fundamental property unchanged. But nobody could prove this was always true.
In February, together with Daniel Ruberman of Brandeis University, Hughes constructed a sequence of counterexamples — “crazy” two-dimensional surfaces that dissect their parent manifolds in ways that mathematicians had believed to be impossible. The counterexamples show that four-dimensional manifolds are even more remarkably diverse than mathematicians in earlier decades had realized. “It’s really a beautiful paper,” Mrowka said. “I just keep looking at it. There’s lots of delicious little things there.”
Making a List
Late last year, Ruberman helped organize a conference that created a new list of the most significant open problems in low-dimensional topology. In preparing for it, he looked at a previous list of important unsolved topological problems from 1997. It included a question that Kronheimer had posed based on his work with Mrowka. “It was in there, and I think it was a little bit forgotten,” Ruberman said. Now he thought he could answer it.
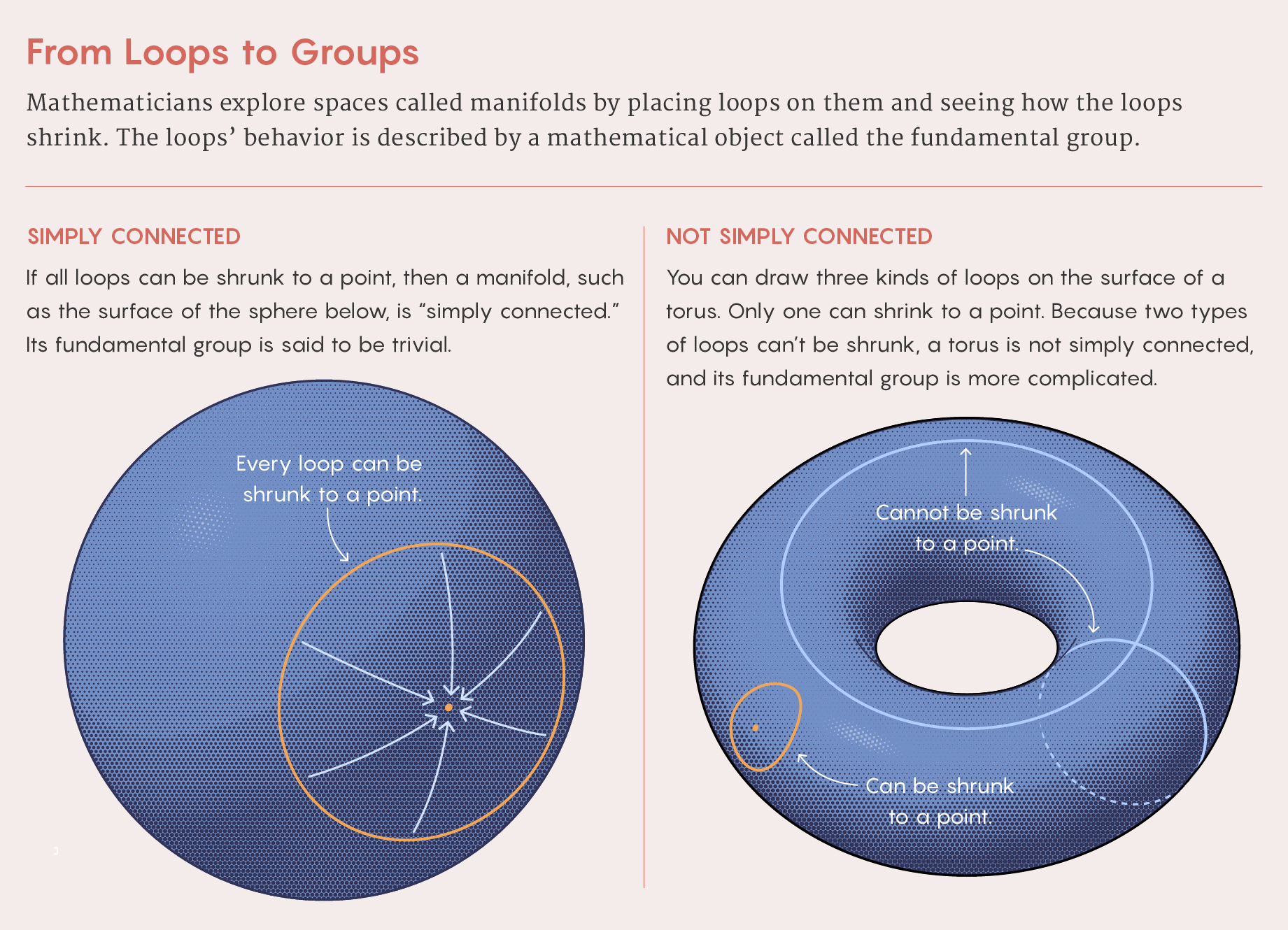
To understand the question, it helps to first consider two key ideas: simply connected manifolds, and the fundamental group.
Simply connected manifolds are spaces without any holes passing through them. In one dimension, an infinite line is simply connected, but a circle isn’t. In two dimensions, an infinite plane and the surface of a sphere are simply connected, but the surface of a doughnut is not.
Mathematicians make this distinction rigorous by placing loops on a manifold and considering how they can be deformed. If any loop can be shrunk to a point, then a manifold is simply connected. On a plane or the surface of a sphere, for instance, this is possible — think about pulling a string taut. But if that string goes around a circle, it can’t shrink. Similarly, on the surface of a doughnut, loops that go either around or through the central hole can’t be deformed into a single point. The doughnut itself gets in the way.
Mathematicians classify spaces that are not simply connected by computing their “fundamental group,” an object whose structure reflects how loops shrink. Manifolds that are simply connected have a “trivial” fundamental group with just one element. But manifolds with holes in them have more complicated fundamental groups.

Merrill Sherman/Quanta Magazine
Merrill Sherman/Quanta Magazine
Four-dimensional manifolds that are simply connected can still be plenty strange. To understand them, mathematicians ponder what can happen to the two-dimensional surfaces embedded in them.
By analogy, think about laying a loop of string flat on a piece of paper. There’s not much you can do with it. But lift it up into three-dimensional space, and you can tie it into complicated knots. The ways in which you can manipulate the string — a one-dimensional manifold — clarify the nature of the space it is embedded in.
Similarly, in the more complicated world of four dimensions, two-dimensional surfaces are “kind of key to the whole business, in many different ways,” Ruberman said. “Surfaces tell you much more about a four-dimensional manifold than you have any right to expect.” Surfaces let you distinguish between manifolds: If a surface can live inside one manifold but not another, you know the manifolds are different. And surfaces can be used to build new manifolds out of old ones.
Surfaces also have corresponding fundamental groups. And so do their complements — the part of a manifold that is left over when you take the surface away. Remove the equator from two-dimensional manifolds like the surface of a sphere or doughnut, for instance, and you get two disconnected halves. But the doughnut’s surface remains in one piece if you remove a vertical ring instead of a horizontal one. Similarly, depending on how you cut a surface out of a four-dimensional manifold, you can get different kinds of complements.
Merrill Sherman/Quanta Magazine
Back in the 1990s, Mrowka and Kronheimer investigated what happens when you excise a two-dimensional surface from a four-dimensional manifold. If the manifold itself is simply connected, what conditions must surfaces meet to guarantee that their complements must also be simply connected?
Kronheimer and Mrowka knew that some kinds of surfaces could have complements that weren’t simply connected. But their work seemed to indicate that another broad class of surfaces must always have simply connected complements.
For nearly three decades, nobody could find an example of a surface in that class whose complement was not simply connected. But in the fall of 2023, after coming across the problem, Ruberman thought he could. Instead of starting with a four-dimensional manifold and cutting out a surface, he began with a two-dimensional surface that had the necessary properties and built a manifold around it.
First, he fattened the surface into a four-dimensional blob. This four-dimensional blob had a three-dimensional boundary, just as a three-dimensional object like a ball has a two-dimensional boundary. Ruberman wanted to attach a carefully chosen four-dimensional manifold to the other side of the boundary, which would serve as the surface’s complement. If the gambit worked, then this manifold would have a complicated fundamental group, yet the fundamental group of everything taken together would be trivial. The newly constructed four-dimensional manifold would therefore be simply connected.
But to be able to glue everything together in the right way, he had to show that the fundamental group of the new addition satisfied all sorts of properties. “I had no idea how to do that,” Ruberman said.
Then in January, Hughes — a group theorist — gave a talk at Brandeis. Ruberman was in the audience. He recognized that Hughes might have the missing piece he was looking for. The two met up the following day, and within a few hours, they’d worked out the main ideas they needed. What Ruberman was missing “is something group theorists have been computing for 70, 80 years at this point,” Hughes said. “We’ve been at this forever.” By the end of the week, they had a completed proof.
“I knew some things, and he knew some things, and between the two of us, we knew enough to just do it,” Ruberman said.
Because of the way group theory gets used in the proof, “it’s a little bit unusual,” said Maggie Miller of the University of Texas, Austin. “It’s written a little bit different than most four-dimensional topologists would be comfortable with.”
The result is yet another example of how complicated four-dimensional topology can get. “There are more interesting embeddings of surfaces than we thought,” Hughes said. This makes it more difficult to classify manifolds, and harder to prove other kinds of results about them.
Nevertheless, in March, İnanç Baykur of the University of Massachusetts, Amherst, who organized last year’s list-making conference with Ruberman, announced the solution to another problem involving simply connected four-dimensional manifolds from the 1997 list.
It seems the topologists are cleaning house.
Correction: April 23, 2024
The original version of this article said that if you slice a sphere or a doughnut in two, you get two hemispheres. It is more accurate to call them halves.



