Math’s ‘Bunkbed Conjecture’ Has Been Debunked
Irene Pérez for Quanta Magazine
Introduction
Much of mathematics is driven by intuition, by a deep-rooted sense of what should be true. But sometimes instinct can lead a mathematician astray. Early evidence might not represent the bigger picture; a statement might seem obvious, only for some hidden subtlety to reveal itself.
Unexpectedly, three mathematicians have now shown that a well-known hypothesis in probability theory called the bunkbed conjecture falls into this category. The conjecture — which is about the different ways you can navigate the mathematical mazes called graphs when they’re stacked on top of each other like bunk beds — seemed natural, even self-evident. “Anything our brain tells us suggests the conjecture should be true,” said Maria Chudnovsky, a graph theorist at Princeton University who was not involved in the new work.
But they were wrong. Last month, a trio of mathematicians announced a counterexample, disproving the conjecture. The result offers fresh guidance on how to approach related problems in physics about properties of solid materials. But it also taps into deeper questions about how mathematics works. A lot of mathematical effort is spent trying to prove conjectures true. It’s lonelier to try to pull them apart. The team behind the new work failed many times before they finally found their counterexample. Their story suggests that mathematicians may need to question their assumptions more often.
Graphs on Graphs
In the mid-1980s, a Dutch physicist named Pieter Kasteleyn wanted to mathematically prove an assertion about how liquids flow throughout porous solids. His work led him to pose the bunkbed conjecture.
To understand it, start with a graph: a collection of points, or vertices, connected by lines, or edges.
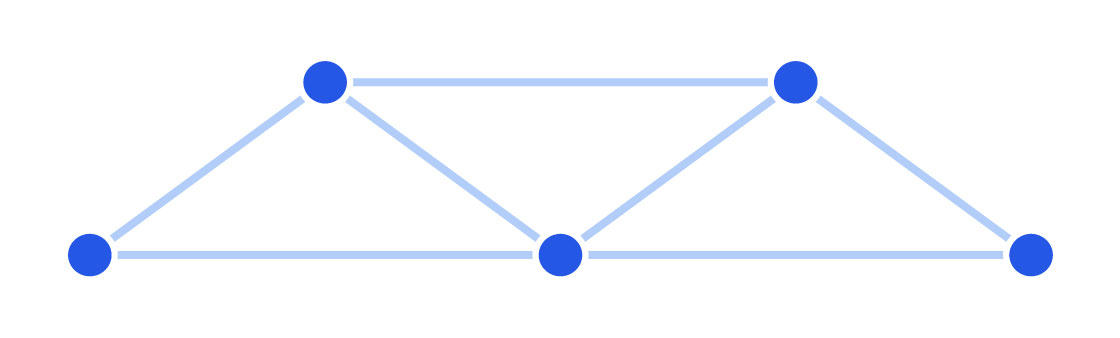
Mark Belan/ Quanta Magazine
Now make an exact copy of the graph and place it directly above the original. Draw some vertical posts between them — additional edges that connect some of the vertices on the bottom graph with their twin vertices on the top graph. The structure you end up with resembles a bunk bed.
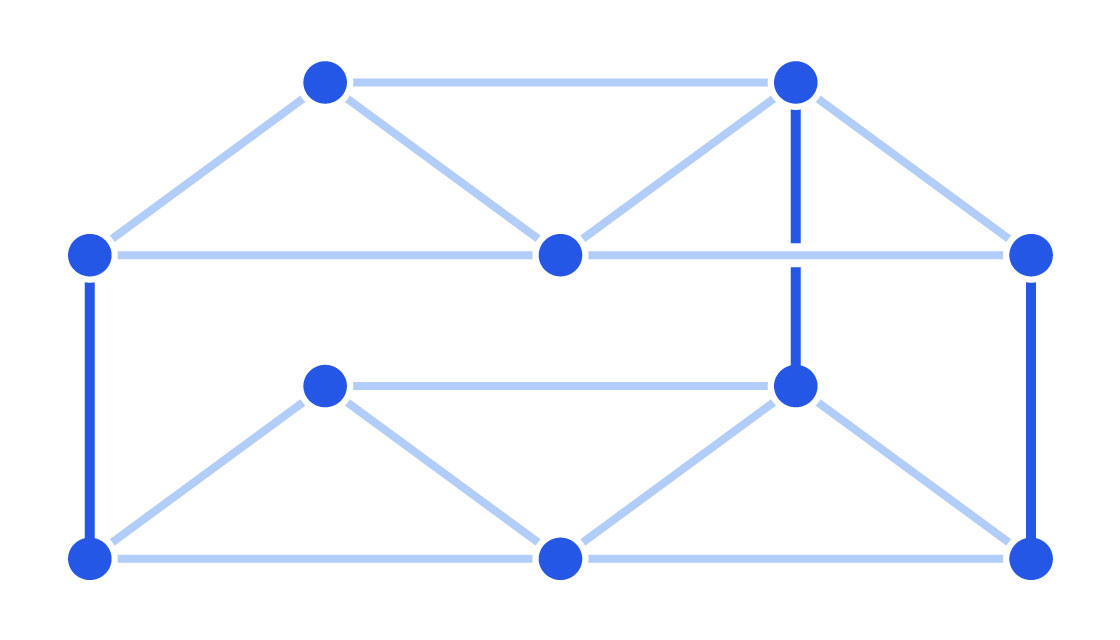
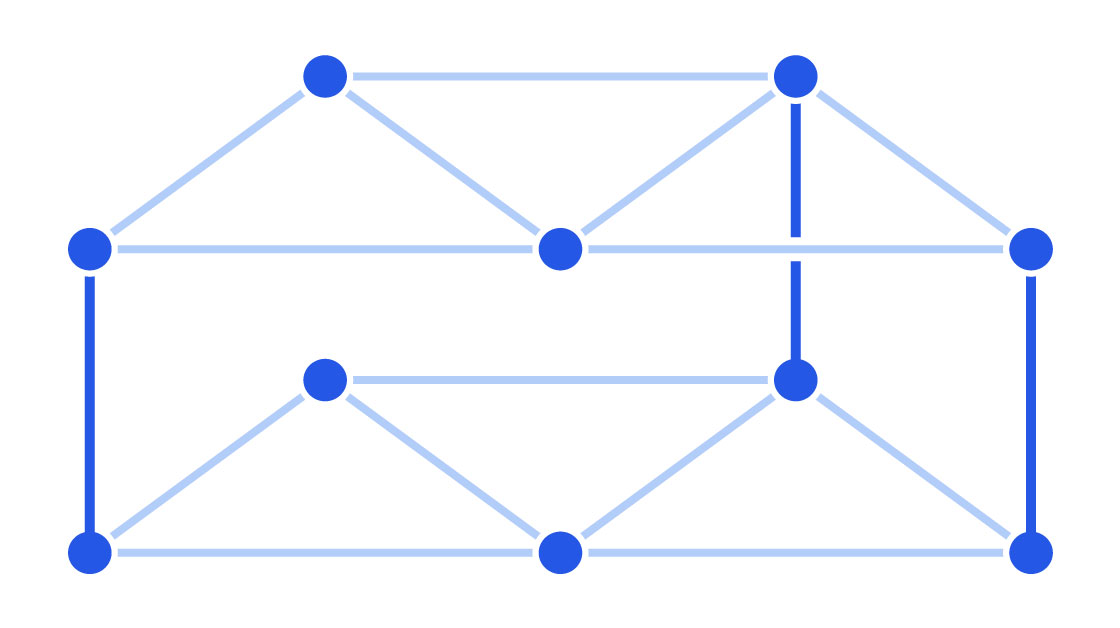
Next, consider an edge in the bottom graph. Flip a coin. If it lands on heads, erase the edge. If it lands on tails, keep the edge. Repeat this process for every edge in both graphs. Your bottom and top bunks will end up looking different, but they’ll still be connected by the vertical posts.
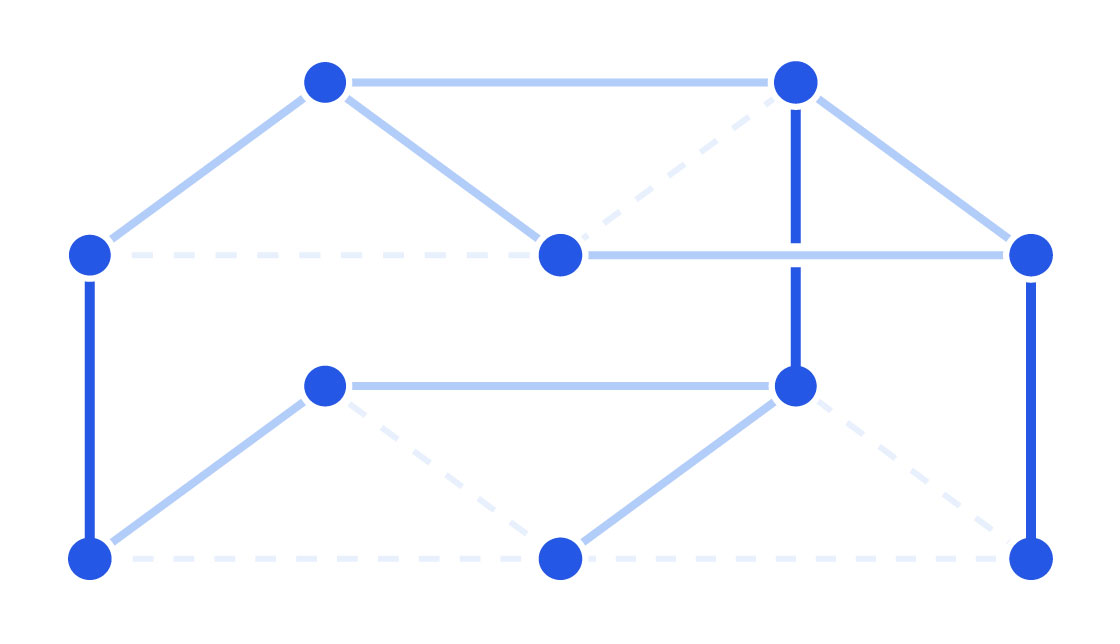
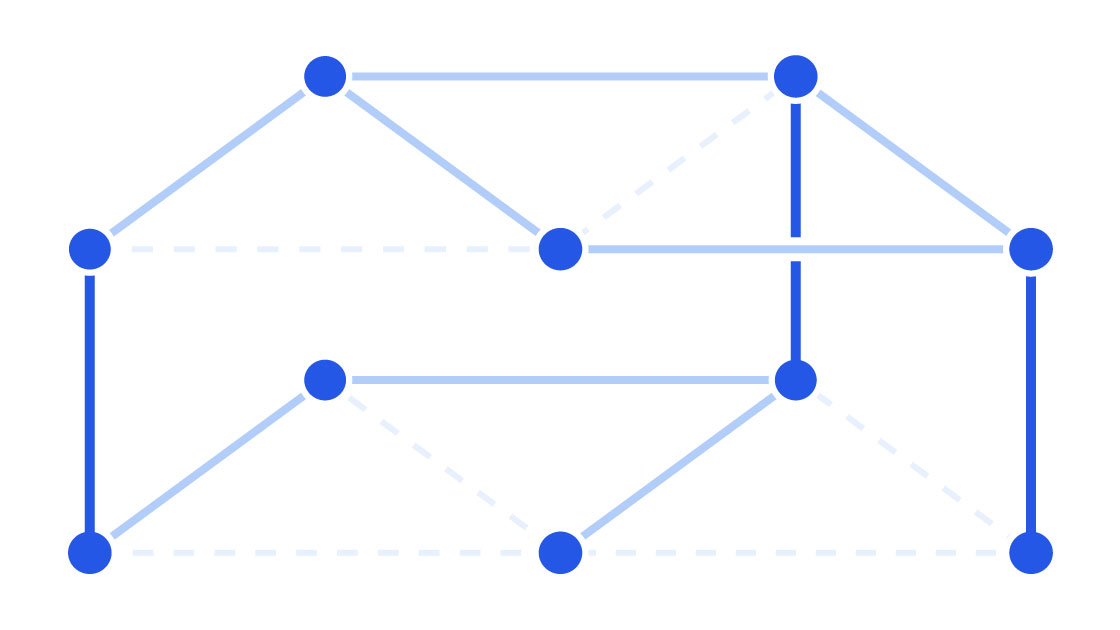
Finally, pick two vertices in the bottom graph. Can you get from one vertex to the other by following the graph’s edges, or are the two now disconnected? For any graph, you can calculate the probability that there will be a path. Now look at the same two vertices, but for one of them, jump up to the vertex directly above it in the top graph. Is there a path that will take you from the starting vertex on the bottom graph to the ending vertex on the top graph?
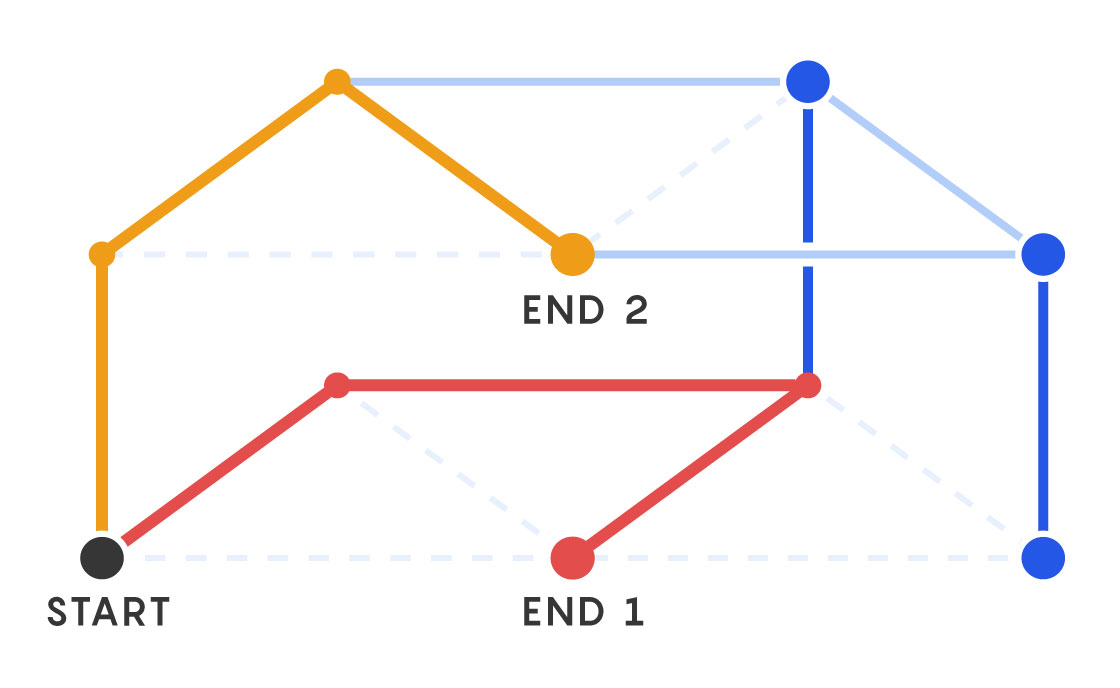
The bunkbed conjecture says that the probability of finding the path on the bottom bunk is always greater than or equal to the probability of finding the path that jumps to the top bunk. It doesn’t matter what graph you start with, or how many vertical posts you draw between the bunks, or which starting and ending vertices you choose.
For decades, mathematicians thought this had to be true. Their intuition told them that moving around on just one bunk should be easier than moving between two — that the extra vertical jump required to get from the lower to the upper bunk should significantly limit the number of available paths.
Mathematicians also wanted the bunkbed conjecture to be true. It belongs to a class of statements in an area called percolation theory, which deals with the paths and clusters that exist after graphs have edges deleted at random. These graphs can be thought of as simplified models of how a fluid moves, or percolates, through a porous material, the way water moves through a sponge. The bunkbed conjecture, for its part, would imply a widely believed assumption in physics about how likely a fluid is to travel through a solid. It would also hint at how to solve related problems about the physics of percolation.
But that would only happen if someone could prove that the bunkbed conjecture was true. There was a reason why no one could.
Probably Wrong
Igor Pak, a mathematician at the University of California, Los Angeles, always had his doubts that the bunkbed conjecture was true. “He was skeptical from the very beginning,” said Nikita Gladkov, one of his graduate students. “He’s a big disbeliever in old conjectures.” Pak has been a vocal critic of mathematicians’ tendency to focus their efforts on proving such conjectures. He asserts that equally important advances can come from asking, “What if they are all wrong?”
Pak also had a particular reason for doubting the bunkbed conjecture: It seemed to be far too broad a claim. He was skeptical that it would really hold for every conceivable graph. “Some conjectures are motivated by substance, and other conjectures are motivated by wishful thinking,” he said. The bunkbed conjecture seemed like the latter.

Nikita Gladkov ran an exhaustive, brute-force search on every graph to search for a counterexample.
Alexey Tregubov
In 2022, he set out to disprove it. He spent a year making failed attempts. Then he instructed Gladkov to use a computer to run an exhaustive, brute-force search on every graph he could. Realizing the task would require some sophisticated programming, Gladkov enlisted a friend he’d known since high school, Aleksandr Zimin, now a graduate student at the Massachusetts Institute of Technology. “We actually were roommates in college — we had a real bunk bed in our dorm,” Gladkov said.
Gladkov, Pak and Zimin were able to manually check every possible graph with fewer than nine vertices. In these cases, they could verify that the bunkbed conjecture held true. But for larger graphs, the number of possible situations blew up. They couldn’t account for all the possible ways that edges could be deleted or paths could be formed.
The team then turned to machine learning. They trained a neural network to produce graphs with circuitous paths that might potentially prefer the upward jump. In many of the examples it spat out, they found that a bottom-bunk path was only the tiniest bit more probable than its top-bunk alternative. But the model didn’t uncover any graphs where the reverse was true.
There was another problem. Each graph the neural network came up with was still so large that the mathematicians couldn’t possibly investigate every single outcome of the coin-flipping step. Rather, the team had to compute the probability of finding upper and lower paths over a subset of these outcomes — much as polls sample from a subset of voters to predict the result of an election.
The mathematicians realized that they could be more than 99.99% confident in any counterexample their neural network gave them — but not 100%. They began to doubt whether pursuing this approach to the problem would be rewarded. It was unlikely to convince the mathematical community; certainly no prestigious journal would consider it a rigorous proof. “Ph.D. students need jobs in reality, not in theory,” Pak wrote on his blog — and Gladkov and Zimin would be looking for jobs soon. “That is really why we stopped,” he continued. “Why persevere and create controversy when you can just try doing something else?”
They gave up on their computational approach, but they didn’t stop thinking about the problem. For the next several months, they focused on formulating a theoretical argument that wouldn’t require a computer. But they didn’t have all the pieces they needed to complete it.
Then a breakthrough came from abroad.
Who Needs Computers?
In June, Lawrence Hollom of the University of Cambridge disproved a version of the bunkbed problem in a different context. Instead of dealing with graphs, this formulation of the conjecture asked about objects called hypergraphs. In a hypergraph, an edge is no longer defined as the connection between a pair of vertices, but rather as the connection between any number of vertices.
Hollom found a counterexample to this version of the conjecture. He created a small hypergraph whose edges each connected three vertices:
Gladkov came across the paper and realized it was just what the trio needed. “I found it in the evening, and I read it until 3 a.m. I was like, ‘Wow, this is crazy. Absolutely mind-boggling,’” he said. He texted Zimin before going to sleep, and the two got on the phone the next day. Could they rework Hollom’s counterexample into a normal graph that would disprove the original bunkbed conjecture?
This wasn’t the first time the pair of old friends had thought about how to translate hypergraphs into graphs. Early last year, they had discussed the issue just before attending a concert together. “The Red Hot Chili Peppers were singing, and I was thinking about this problem,” Gladkov said. “I was not listening to the music much.” They later developed techniques that allowed them to move from hypergraphs to graphs in particular situations.
They could now use those techniques, they realized, to adapt Hollom’s hypergraph. Gladkov, Pak and Zimin replaced each three-vertex edge in the hypergraph with a massive cluster of points and normal edges. This gave them an enormous graph of 7,222 vertices connected by 14,422 edges. They then used the theoretical argument they’d built up after abandoning their artificial intelligence approach to prove that in this graph, finding an upper path was $latex \frac{1}{10^{6,500}}$ percent more likely than finding a lower one — an unimaginably small but nonzero number. The bunkbed conjecture was wrong.
Their result shows the importance of not taking anything for granted, said Noga Alon, a mathematician at Princeton. “We have to be suspicious, even about things that intuitively look very likely to be true.”
Gladkov, Pak and Zimin found many small-graph examples that satisfied the conjecture, but in the end, those did not reflect the more complicated, less intuitive graphs they could build when given enough vertices and edges.
As Hollom put it, “Do we actually understand all this stuff as well as we think we do?”
Mathematicians still believe the physics statement about connected locations within solids that inspired the bunkbed conjecture. But they’ll need to find a different way to prove it.
In the meantime, Pak says, it’s clear that mathematicians need to engage in a more active discussion about the nature of mathematical proof. He and his colleagues ultimately didn’t have to rely on controversial computational methods; they were able to disprove the conjecture with total certainty. But as computer- and AI-based lines of attack become more common in mathematics research, some mathematicians are debating whether the field’s norms will eventually have to change. “It’s a philosophical question,” Alon said. “How do we view proofs that are only true with high probability?”
“I think the future of mathematics will be to accept probabilistic proofs like this,” said Doron Zeilberger, a mathematician at Rutgers University who is known for crediting his computer as a co-author on many of his papers. “In 50 years, or maybe less, people will have a new attitude.”
Others wonder if such a future threatens something vital. “Maybe a probabilistic proof would give you less understanding or intuition of what’s really going on,” Alon said.
Pak has suggested that separate journals be created for results of this kind as they become more common, so that their value isn’t lost to mathematicians. But his main goal is to open the conversation. “There’s no correct answer,” he said. “I want the community to meditate on whether the next result of this kind will count.” As technology continues to infiltrate and transform mathematics, the question will only become more pressing.



