Merging Fields, Mathematicians Go the Distance on Old Problem
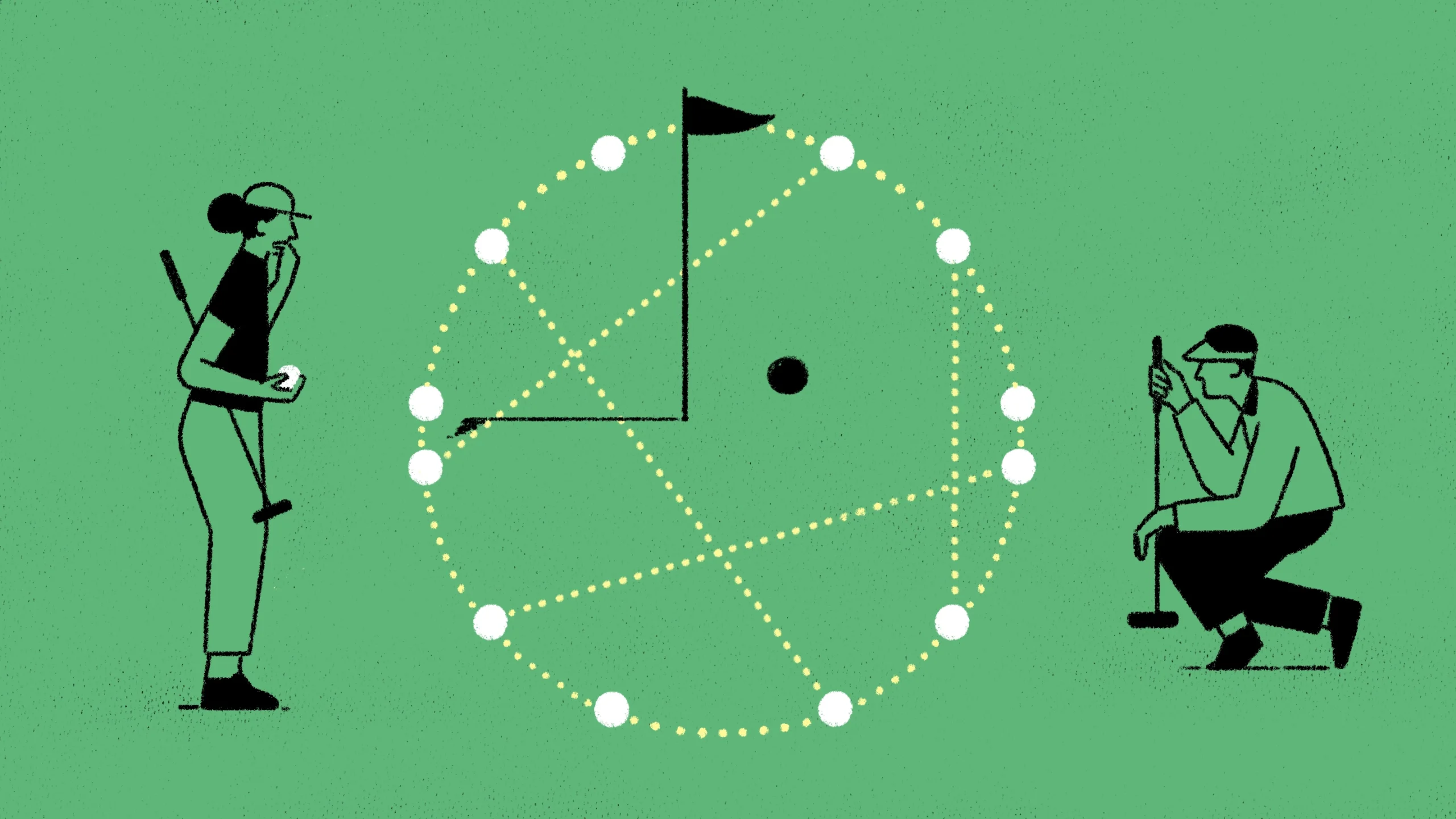
If a large (but non-infinite) set of points are whole-number distances away from each other, how can they be arranged? A new result proves that a circle is one of the only options.
Fran Pulido for Quanta Magazine
Introduction
The change of plans came on a road trip. On a beautiful day last April, the mathematicians Rachel Greenfeld and Sarah Peluse set out from their home institution, the Institute for Advanced Study in Princeton, New Jersey, heading to Rochester, New York, where both were scheduled to give talks the next day.
They had been struggling for nearly two years with an important conjecture in harmonic analysis, the field that studies how to break complex signals apart into their component frequencies. Together with a third collaborator, Marina Iliopoulou, they were studying a version of the problem in which the component frequencies are represented as points in a plane whose distances from each other are related to integers. The three researchers were trying to show that there couldn’t be too many of these points, but so far, all their techniques had come up short.
They seemed to be spinning their wheels. Then Peluse had a thought: What if they ditched the harmonic analysis problem — temporarily, of course — and turned their attention to sets of points in which the distance between any two points is exactly an integer? What possible structures can such sets have? Mathematicians have been trying to understand integer distance sets since ancient times. For example, Pythagorean triples (such as 3, 4 and 5), represent right triangles whose three vertices are all integer distances apart.
“In the car, I guess because Rachel was trapped with me, I brought it up,” said Peluse, who is now a professor at the University of Michigan. The idea of tackling integer distance sets electrified Greenfeld.
Before they knew it, they had embarked on not one change of direction but two.
“We actually stopped paying attention to where we were going and didn’t get off the expressway,” Peluse said. “We were going in the opposite direction from Rochester for, like, an hour before we noticed, because we were so excited about the math.”
In 1945, Norman Anning and Paul Erdős proved that an infinite set of points in the plane that are all integer distances apart must lie on a line. For a finite set of points, the possibilities are a little more varied. Mathematicians have constructed large sets that lie on either a line or a circle, sometimes with three or four extra points that are off the main drag. (The points themselves don’t have to have integer coordinates — the question is about the distances between them.)

Rachel Greenfeld, a mathematician at the Institute for Advanced Study.
Andrea Kane
No one has come up with a large set of points with any other configuration, but nobody has proved that other configurations are impossible. In the nearly 80 years since Anning and Erdős’ result, the subject has seen virtually no progress — until now.
Greenfeld, Iliopoulou and Peluse have proved that all the points in a large integer distance set — except perhaps a sparse handful of outlier points — must lie on a single line or circle. “If you want to have a large set where all the pairwise distances are integers, then circles and lines are the only players,” said József Solymosi of the University of British Columbia. He called their result a “fantastic solution.”
The new approach uses ideas and techniques from three distinct areas of mathematics: combinatorics, number theory and algebraic geometry. This joining together of different fields “could be a real psychological breakthrough,” said Terence Tao, a mathematician at the University of California, Los Angeles.
Alex Iosevich, of the University of Rochester, agrees. “They laid down a very solid foundation for a very broad set of problems,” he said. “There’s absolutely no doubt in my mind that this is going to find even deeper applications.”
The Limits of Simplicity
Within a plane, it’s easy to choose an infinite set of points that are all integer distances apart — just take your favorite line, imagine a number line superimposed on it, and use some or all of the points corresponding to whole numbers. But this is the only way to construct an infinite integer distance set in the plane, as Anning and Erdős realized in 1945. As soon as you have just three points that are not all on the same line, your configuration becomes so constrained that it’s impossible to add infinitely many more points.
The reason boils down to simple geometry. Imagine starting with two points, A and B, that are an integer distance apart. If you want to add a third point, C, that is an integer distance from both A and B but doesn’t lie on the line through them, most points in the plane won’t work. The only viable points live on special curves called hyperbolas that cut between A and B. If A and B are, say, 4 units apart, then there are exactly four of these hyperbolas. (A hyperbola usually has two distinct parts, so for example the two red curves in the figure below form a single hyperbola.)
Merrill Sherman/Quanta Magazine
Once you’ve chosen C (which in this example is 3 units from A and 5 units from B), you have hardly any options for adding more points. Any point you could add must lie on one of the hyperbolas between A and B, or on the line that runs through them. But it must also lie on one of the hyperbolas between A and C, and one of the hyperbolas between B and C (or the corresponding lines) — in other words, a new point can only be placed where three hyperbolas or lines intersect (though not every intersection point will work). There are only finitely many of these hyperbolas and lines to begin with, and two hyperbolas (or lines) can intersect in at most four points. So you end up with only finitely many intersection points to choose from — you can’t build an infinite set.
When it comes to understanding what a finite set of integer distance points actually looks like, the hyperbola approach quickly gets unwieldy. As you add points, you have to grapple with growing numbers of hyperbolas. For instance, by the time your set has just 10 points, adding an 11th will create 10 new families of hyperbolas — all the ones between your new point and each of the points already in the set. “You cannot add many points, because you’ll get lost in all those hyperbolas and intersections,” Greenfeld said.
So mathematicians have looked for more manageable principles for constructing large sets of integer distance points that don’t lie on a line. But they’ve only been able to come up with one approach: Put your points on a circle. If you want an integer distance set with, say, a trillion points, there are ways to come up with a trillion points on a circle of radius 1 whose distances apart are all fractions. Then you can inflate the circle until all the fractional distances turn into whole numbers. The more points you want in your set, the more you’ll need to inflate the circle.
Over the years, mathematicians have come up with only slightly more exotic examples. They can construct large integer distance sets in which all but four points lie on a line or all except three lie on a circle. Many mathematicians suspect that these are the only large integer distance sets in which not all of the points are on a line or a circle. They’ll know this for sure if they can ever prove something called the Bombieri-Lang conjecture. But mathematicians are divided about whether this conjecture is likely to be true.
Since Anning and Erdős’ work in 1945, mathematicians have made little progress on understanding integer distance sets. Over time, the integer distance problem seemed to join an array of other problems in combinatorics, number theory and geometry that are simple to state but seemingly impossible to solve. “It’s a measure of how pathetic our mathematics is,” Tao said.

Sarah Peluse, a mathematician at the University of Michigan.
Dan Komoda
In a way, the integer distance problem was a victim of its own early successes. The hyperbola proof, with its ingenious simplicity, is emblematic of the philosophy espoused by Erdős, a highly influential mathematician who often spoke of “The Book” — an imagined volume of the most elegant proofs in mathematics. The culture of simplicity Erdős promoted has led to “tremendous results” in combinatorial geometry, Iosevich said. But it can also lead to blind spots — in this case, about the value of bringing in approaches from algebraic geometry.
“I don’t think you will find a result [in algebraic geometry] proven in the last 50 years that is not very technically involved and messy,” Iosevich said. “However, sometimes things need to be this way.”
In retrospect, the integer distance problem was waiting for mathematicians who were willing to consider more unruly curves than hyperbolas and then draw on recondite tools from algebraic geometry and number theory to tame them. “It required people with a sufficient breadth of knowledge and interest,” Iosevich said.
Most mathematicians, he said, are content to ply a few tools in one corner of mathematics for their entire career. But Greenfeld, Iliopoulou and Peluse are fearless explorers, Iosevich said. “They view mathematics as a coherent whole.”
Complexifying the Problem
In the summer of 2021, Greenfeld decided that it was time to take a stab at a problem from harmonic analysis she’d been mulling over since graduate school. Classical harmonic analysis, which forms the foundation for signal processing in the real world, is all about decomposing signals into sine waves of different frequencies and phases. This process works because it’s possible to make an infinite list of sine waves that, when combined, capture all the features of any signal, without any redundancy.
Often, though, researchers want to study something more complicated than a one-dimensional signal. For instance, they might want to decompose a signal on a disk in the plane. But the disk can only host a finite collection of compatible sine waves — too few to capture the behavior of all possible signals on the disk. The question then becomes: How big can this finite collection be?
In such a collection, the frequencies of the sines can be represented as points in the plane that seem averse to clustering in lines and circles: You’ll never find three points that are all close to the same line, or four that are all close to the same circle. Greenfeld hoped to use this aversion to prove that these sets of frequencies can contain only a few points.
At a 2021 meeting at the University of Bonn, Greenfeld attended a talk about the “determinant method,” a technique from number theory that can be used to estimate how many integer points of certain types can lie on curves. This tool, she realized, might be just what she needed. Greenfeld recruited Iliopoulou and Peluse, who were also at the meeting. “We started to learn this method together,” Greenfeld said.
But despite many efforts, they couldn’t seem to bend the determinant method to their purpose, and by the spring of 2023, they were feeling discouraged. Iosevich had invited Greenfeld and Peluse to drive to Rochester for a visit. “So we were thinking, ‘OK, we’ll go to Rochester, and talking to Alex will reinvigorate us,’” Peluse said. But as it turned out, they landed in Rochester already reinvigorated, thanks to a bracing discussion of integer distance sets on their unplanned detour along the Susquehanna River in Pennsylvania.
They arrived too late for a planned dinner with Iosevich, but they found him waiting in the hotel lobby with bags of takeout. He forgave their lateness — and was more than forgiving the next morning, when they told him about their plan to tackle integer distance sets. “He was so excited,” Peluse recalled. “Emotionally, this was a huge boost.”
As with the hyperbola approach, Greenfeld, Iliopoulou and Peluse tried to control the structure of integer distance sets by identifying families of curves the points must lie on. The hyperbola method starts to get too convoluted as soon as you have more than a few points, but Greenfeld, Iliopoulou and Peluse figured out how to consider many points at the same time by moving the entire configuration into a higher-dimensional space.
To see how this works, suppose you start with a “reference” point A in your integer distance set. Every other point in the set is an integer distance from A. The points live in a plane, but you can bump the plane into three-dimensional space by tacking a third coordinate onto each point, whose value is the distance from A. For instance, suppose A is the point (1, 3). Then the point (4, 7), which is 5 units away from A, turns into the point (4, 7, 5) in three-dimensional space. This process converts the plane into a cone in three-dimensional space whose tip sits at A, now labeled (1, 3, 0). The integer distance points become points in three-dimensional space that lie on the cone and also on a certain lattice.
Similarly, if you choose two reference points, A and B, you can convert points in the plane to points in four-dimensional space — just give each point two new coordinates whose values are its distances to A and B. This process converts the plane into a curvy surface in four-dimensional space. You can keep adding more reference points in this way. With each new reference point, the dimension increases by one and the plane gets mapped to an even wigglier surface (or, as mathematicians say, a surface of higher degree).
With this framework in place, the researchers used the determinant method from number theory. Determinants are numbers, usually associated with matrices, that capture a host of geometric properties of a collection of points — for instance, a particular determinant might measure the area of the triangle formed by three of the points. The determinant method offers a way to use such determinants to estimate the number of points that lie simultaneously on a wiggly surface and on a lattice — just the kind of situation Greenfeld, Iliopoulou and Peluse were dealing with.
The researchers used a line of work based on the determinant method to show that when they bump their integer distance set up to a suitably high dimension, the points must all lie on a small number of special curves. These curves, when their shadows in the plane are not a line or a circle, can’t contain many lattice points, which are the only candidates for points in the integer distance set. That means the number of points in the set that can lie off the main line or circle is bounded — the researchers showed that it must be smaller than a very slowly growing function of the set’s diameter.
Their bound doesn’t reach the standard of the “four points off the line or three points off the circle” conjecture that many mathematicians believe is true for large integer distance sets. Even so, the result shows that “the essence of the conjecture is true,” said Jacob Fox of Stanford University. A full proof of the conjecture will likely require another infusion of new ideas, mathematicians said.
The team’s high-dimensional encoding scheme is “extremely robust,” Iosevich said. “There aren’t only applications in principle — there are applications that I’m already thinking about.”
One application, Greenfeld, Iliopoulou and Peluse hope, will be to their original harmonic analysis problem, to which the three are now returning. Their result on integer distance sets “could be a steppingstone toward that,” Greenfeld said.
The synthesis of combinatorics with algebraic geometry that the researchers initiated will not stop with integer distance sets or allied problems in harmonic analysis, Iosevich predicted. “I believe that what we are seeing is a conceptual breakthrough,” he said. “This sends a message to people in both fields that this is a very productive interaction.”
It also sends a message about the value of sometimes making a problem more complicated, Tao said. Mathematicians usually strive for the reverse, he noted. “But this is an example where complexifying the problem is actually the right move.”
The advance has changed the way he thinks about high-degree curves, he said. “Sometimes they can be your friends and not your enemies.”



