New Shapes Solve Infinite Pool-Table Problem

Olena Shmahalo/Quanta Magazine; background: FrostBo
Introduction
Strike a billiard ball on a frictionless table with no pockets so that it never stops bouncing off the table walls. If you returned years later, what would you find? Would the ball have settled into some repeating orbit, like a planet circling the sun, or would it be continually tracing new paths in a ceaseless exploration of its felt-covered plane?
These kinds of questions occurred to mathematical minds centuries ago, in relation to the long-term trajectories of real objects in outer space, and for nearly that long they’ve seemed impossible to determine exactly. What will a bouncing ball be up to a billion years from now? It’s as hard to answer as it sounds.
More recently, though, mathematicians have achieved a succession of stunning breakthroughs. One of the latest results, yet to be published, describes a new category of what are known as “optimal” billiard tables — shapes whose particular angles make it possible to understand every billiard path that could occur within them. The newfound shapes are among a handful of optimal billiard tables ever discovered, and part of an even more select group of quadrilaterals with that property.
“They are like these rare jewels,” said Curt McMullen, a mathematician at Harvard University and a co-author of the work along with Alex Wright of Stanford University, Ronen Mukamel of Rice University and Alex Eskin of the University of Chicago.
To find these jewels, these four mathematicians used an elegant set of methods that allow mathematicians to reimagine the claustrophobic, rebounding world of a billiard table as an elegant universe of smooth curves arcing unimpeded through space. There, the far-out future of the billiard path can be apprehended at a glance — while at the same time, perfect billiard tables end up serving as clues about the nature of the exotic higher-dimensional space in which they appear.
The Shape That Wouldn’t Go Away
When you set a ball in motion on a billiard table, it may seem as if anything is possible, but when a table has optimal dynamics, only two things truly are. The first is complete chaos, which is to say that the ball’s path will cover the entire table as time wears on. The second is periodicity — a repeating path like a ball pinging back and forth between two sides.
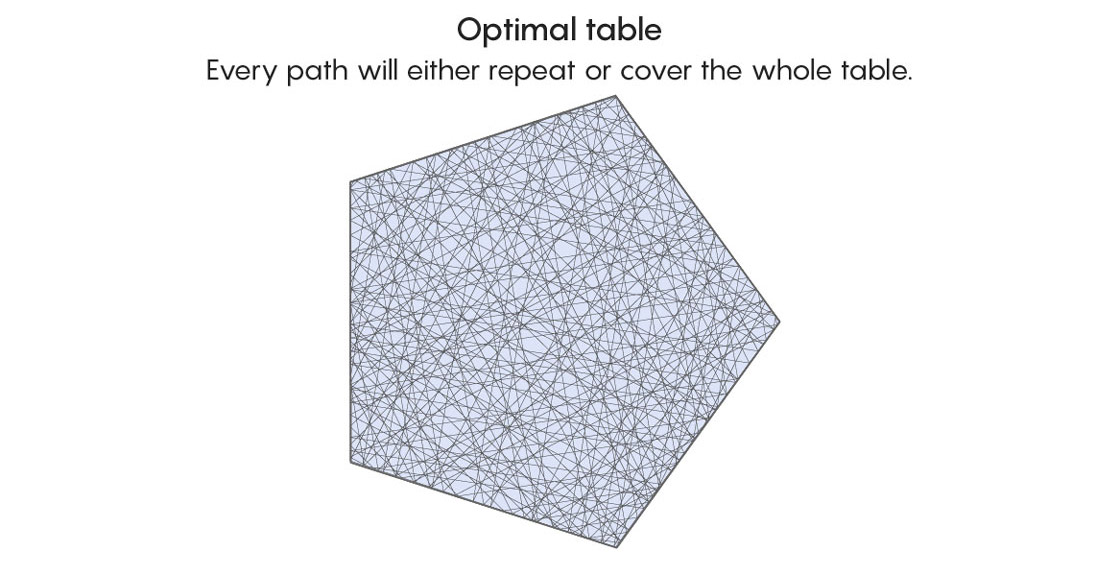
In tables without optimal dynamics, a wider range of possibilities exists, which makes the full analysis of all possible paths impossible: A ball could end up bouncing chaotically in one part of the table forever, never retracing its path, but also never covering the whole table.
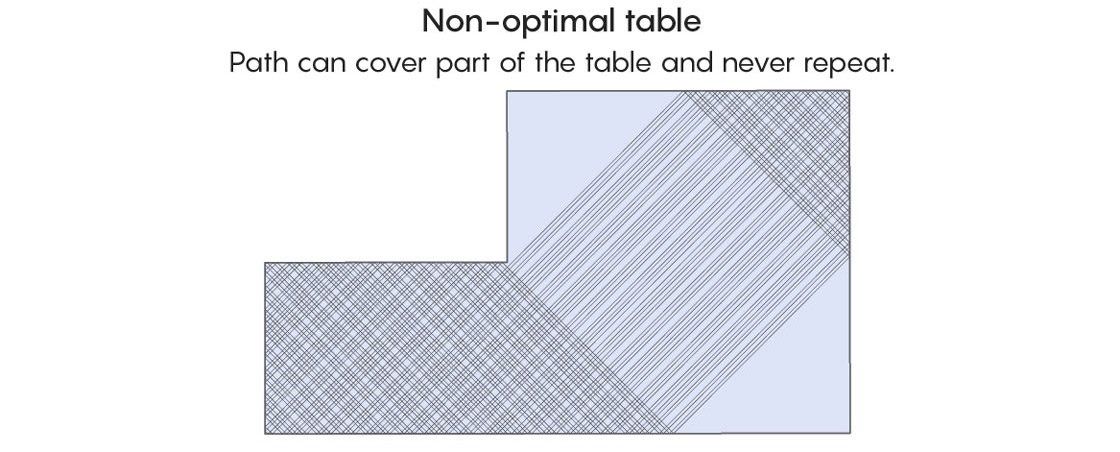
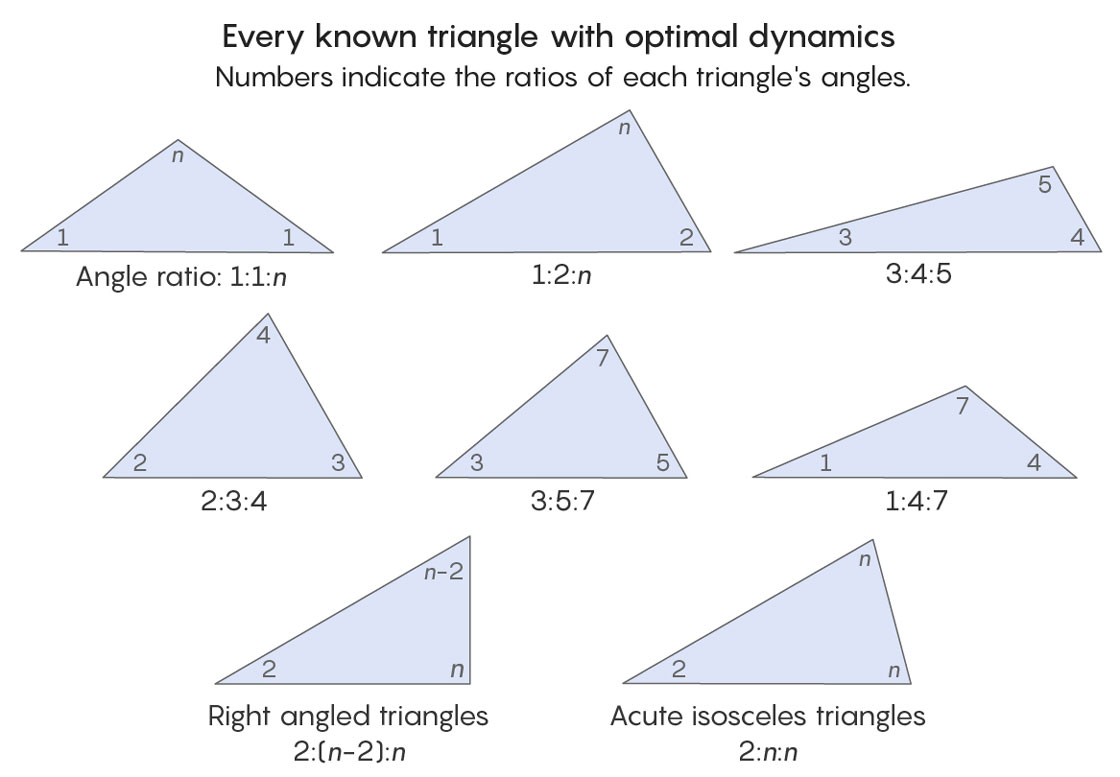
If you’re given a polygon, there’s no easy way to tell if it has optimal dynamics. For this reason, many basic questions about billiard paths remain unanswered. For example, is there at least one periodic trajectory within every possible triangle? Mathematicians can’t say, though they can point to the obstacle.
“There’s a lot that’s not known about obtuse triangles,” McMullen said, adding, “Well, don’t let me get off on a rant about triangles.”
What mathematicians do know is that there are at least eight kinds of triangles with optimal dynamics; the first was discovered in 1989 and the last in 2013. Whether there are more is anyone’s guess. “That may be the last example,” McMullen said.
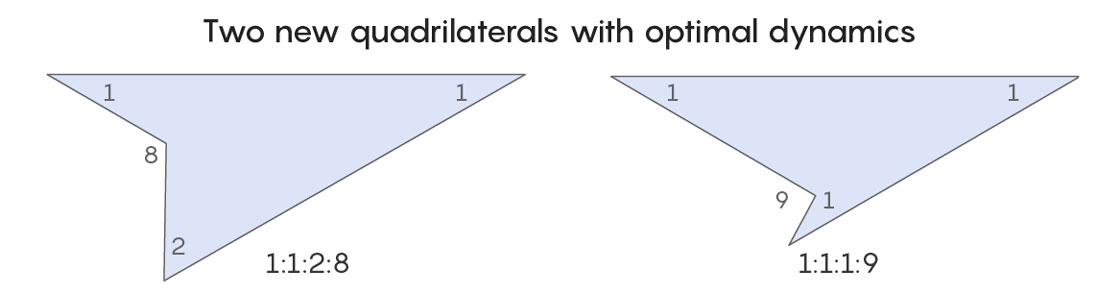
The new article identifies two new families of quadrilaterals with optimal dynamics: quadrilaterals whose angle ratios are 1:1:1:9 and 1:1:2:8. Both resemble darts, with two fins in the back and a point up front, and together they’re the first quadrilaterals with optimal dynamics to be found in a decade.
Wright was the first to glimpse these shapes. In 2014 he was at Stanford University, collaborating with Maryam Mirzakhani, who that year became the first woman to win a Fields Medal (math’s highest honor) and who recently died of cancer at age 40. The two were, in a sense, trying to prove that shapes like these quadrilaterals don’t exist. Wright tried to rule out one example after another by showing that the existence of each particular object would imply a contradiction. But then he came across a shape he just couldn’t make go away.
A Straight-Line Solution
When he began this work, Wright was not actually thinking about quadrilaterals, and he had no particular interest in billiards. Instead, he and Mirzakhani were exploring the properties of a mathematical area called moduli space, which has played a central role in a wide range of mathematical discoveries over the last 50 years.
“Moduli space is a meeting ground where mathematical thought takes place,” McMullen said. “It’s related to string theory, it’s an avatar, an endless source of inspiration.”
In mathematics, it’s often beneficial to study classes of objects rather than specific objects — to make statements about all squares rather than individual squares, or to corral an infinitude of curves into one single object that represents them all.
“This is one of the key ideas of the last 50 years, that it is very convenient to not study objects individually, but to try to see them as a member of some continuous family of objects,” said Anton Zorich, a mathematician at the Institute of Mathematics of Jussieu in Paris and a leading figure in dynamics.
Moduli space is a tidy way of doing just this, of tallying all objects of a given kind, so that all objects can be studied in relation to one another.
Imagine, for instance, that you wanted to study the family of lines on a plane that pass through a single point. That’s a lot of lines to keep track of, but you might realize that each line pierces a circle drawn around that point in two opposite places. The points on the circle serve as a kind of catalog of all possible lines passing through the original point. Instead of trying to work with more lines than you can hold in your hands, you can instead study points on a ring that fits around your finger.
“It’s often not so complicated to see this family as a geometric object, which has its own existence and own geometry. It’s not so abstract,” Zorich said.
Just as the circle can be (roughly) thought of as the moduli space of lines passing through a point, there is a moduli space that relates to billiards by a roundabout process.
Start with a polygon whose billiard paths you’re interested in, and whose angles are rational multiples of pi (a stipulation without which the following steps won’t work). Then start reflecting that polygon over its edges in a process mathematicians call “unfolding.” Continue this reflection process until any further reflection would give you a copy of a polygon you already have.
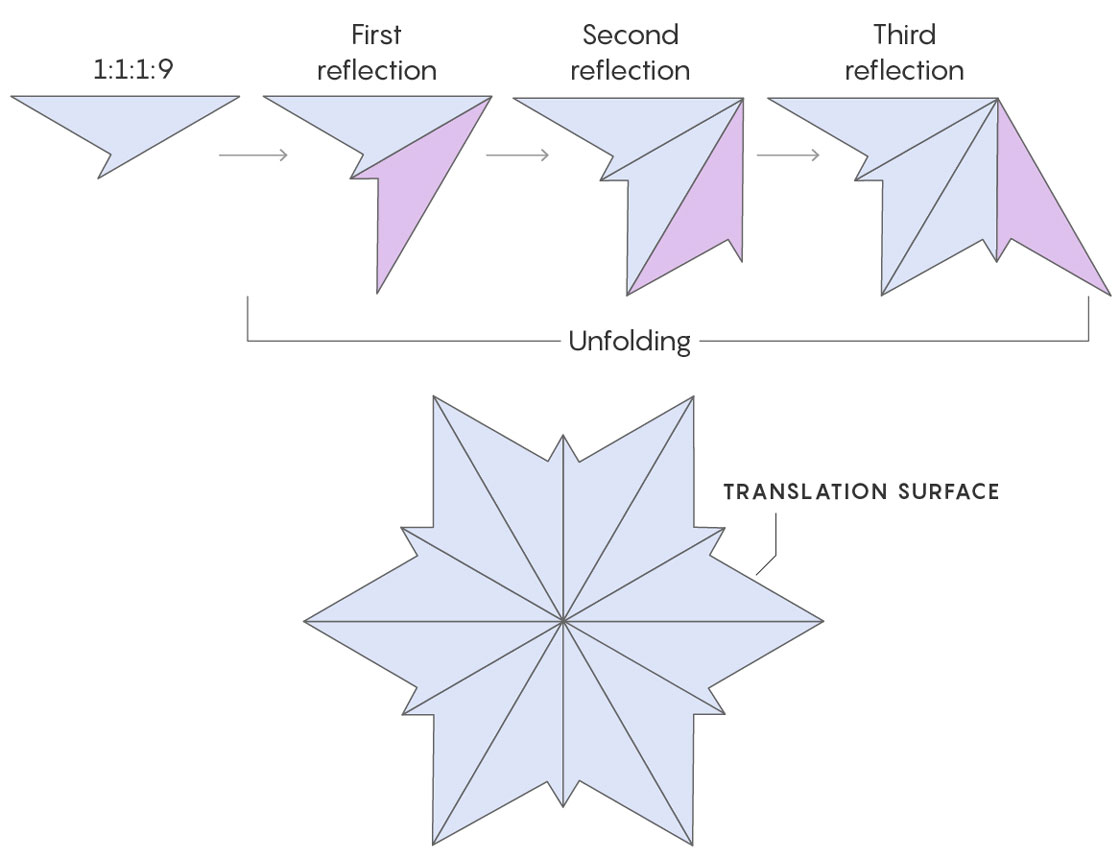
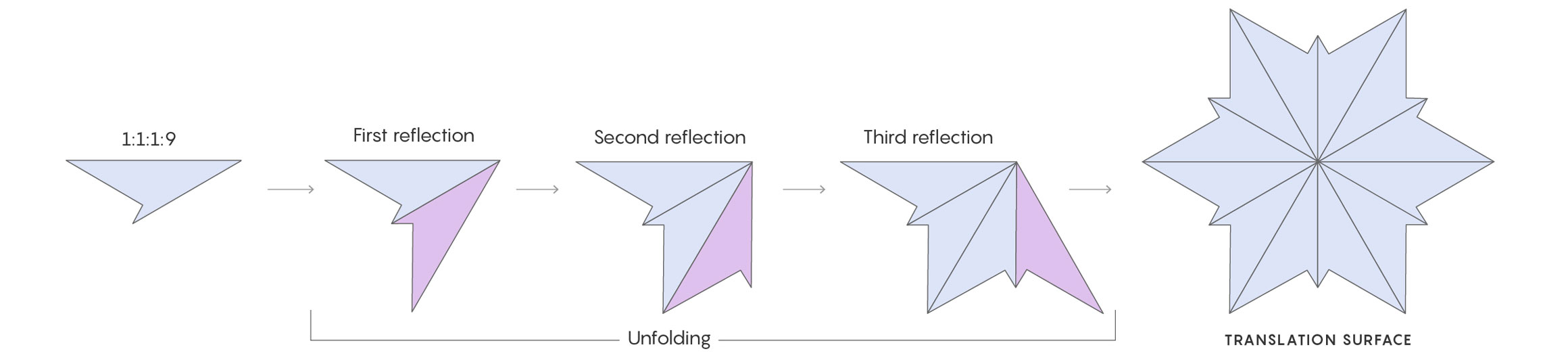
The reflected polygon is now a new shape called a translation surface. And on this surface the behavior of a billiard ball changes. Rather than striking a side of a triangle and bouncing off, the ball moves in a continuous straight line.
“Instead of studying billiards in polygons you end up studying straight-line flows on translation surfaces,” Wright said.
Every translation surface generated by reflecting polygons can be described uniquely by a set of real numbers (the numbers come from mathematical objects called vectors that define the shape). These numbers serve as coordinates in moduli space, where each point represents a different translation surface.
This, then, is the process so far: Start with billiards in a polygon, reflect that polygon to create a translation surface, and encode that translation surface as a point in the moduli space of all translation surfaces. The miracle of the whole operation is that the point in moduli space remembers something of the original polygon — so by studying how that point fits among all the other points in moduli space, mathematicians can deduce properties of billiard paths in the original polygon.
Closing the Orbit
The main way that mathematicians study points in moduli space is by looking at what’s called their “orbit closures,” which is also a way of getting at the properties of the polygons represented by those points.
Mathematicians study orbit closures in moduli space for their own sake, irrespective of anything to do with billiards. At the same time, a clear way to understand the significance of orbit closures is to consider how they’re used in the study of billiards, and how the two — orbit closures and billiard paths — can provide information about each other.
“There is a surprising interaction between algebraic geometry, the pure mathematics of moduli spaces, and the dynamics of billiards, that goes both ways,” said McMullen.
If you’re interested in studying billiard paths in, say, a 1:1:1:9 quadrilateral, one way to do it is to manipulate the associated translation surface using a matrix. A matrix, like the one below, is really just a set of directions for how to change the proportions of the surface — maybe by stretching it in one dimension, shrinking it in another, or tilting it to the left or right. If you start with this square and multiply it by this two-by-two matrix, you deform the square into a right-leaning parallelogram.
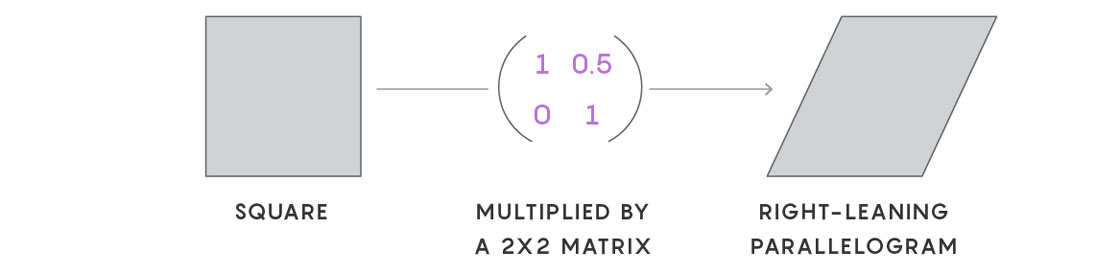
There’s an infinite variety of two-by-two matrices, and if you apply the correct one, it will bring the dynamics of your polygon into focus. Say, for example, you give your billiard ball a push in the vertical direction. You want to know what it is doing 1 million units of time later. If you stretch your polygon by a factor of 1 million in the horizontal direction and shrink it by 1 million in the vertical direction, you effectively zoom in on that far-out behavior. This is a process called renormalization, which is widely used in math and physics.
“If you shrink the space in the direction of the billiard line by a factor of 1 million,” McMullen said, “that radically changes the surface you’re on. But now the analysis of the time-1-million flow is reduced to the analysis of the time-one flow.”
When you transform a translation surface using a matrix, you create downstream effects: The new surface corresponds to a new point in moduli space. Given that, a more direct way to study what’s going on in this matrix transformation is simply to study points in moduli space: We started at this point, used this matrix, and ended up at this other point. The path from the first point to the second is called an orbit. What’s revealing for mathematicians is the so-called “orbit closure,” which is the set of all possible points you can arrive at (or get infinitely close to) when you start at one point and act on it by means of all possible two-by-two matrices.
Mirzakhani won the Fields Medal in large part for discoveries she made about orbits in moduli space, particularly in joint work with Eskin and Amir Mohammadi, who is now at the University of California, San Diego. From a naive perspective, you might assume that orbit closures are completely idiosyncratic, or fractal — in other words, that there’s a totally unique orbit closure for each point in moduli space. Mirzakhani and her co-authors proved that orbit closures in moduli space are actually nice, neat shapes called manifolds, and that there are only a few distinct types of them.
“The fact that they’re very nice manifolds means they’re a simpler, tamer object that can be understood,” Wright said. “Part of Maryam’s insight is that there shouldn’t be so many. The driving sentiment behind her conjectures is that rather than a vast zoo, there should only be a few types and we should be able to classify them.”
In their 2014 work Mirzakhani and Wright came across an orbit closure that didn’t seem to fit in any known categories. Wright went to Eskin, who had earlier collaborated with Mirzakhani and who had developed a computer program for studying billiard paths in polygons. Wright input the point into Eskin’s program. On the first two runs the computer program said there was nothing unique about its orbit closure. But then Wright adjusted some numbers in the program, and the third time through it showed that this orbit closure was as special as he had hoped.
“I’d been inputting data with 20 digits of precision and it needed 40 or something,” he said. “Then I was staring at a perfect output from the program. I literally jumped up and down with excitement, which might be the only time I’ve ever done that doing math.”
Wright then went to Mukamel and McMullen, who helped him come up with an algebraic way of thinking about the problem. With their techniques, the trio was able to prove a related conjecture, and later, with Eskin, they also proved that this new orbit closure really does exist.
“Once we had a handle on the algebraic equations, we could prove there was a variety of the type Alex was seeing hints of,” Mukamel said.
The process they used to investigate the properties of the quadrilateral that had first perplexed Wright eventually led the authors to two new quadrilaterals with optimal dynamics: the 1:1:1:9 and 1:1:2:8 shapes. Both shapes are unassuming, the kinds of funky constructions you might come across in a doodle. But in the rarefied air of moduli space, they have proved to be so much more.
Correction August 8, 2017: An earlier version of the story misidentified the paper that the billiard work appears in. That paper, co-authored by Eskin, McMullen, Mukamel and Wright, is not yet published.



