Solution: Magic Moiré in Twisted Graphene

Dan Page for Quanta Magazine
Introduction
Materials science was rocked recently by an amazing discovery: When a layer of graphene, a sheet of carbon crystal with atoms arranged in a one-atom-thick hexagonal lattice, is dropped on another one and rotated to just the correct angle, the resulting bilayer graphene magically acquires the ability to become superconductive. Our June Insights puzzle explored a set of simple questions designed to give some intuitive understanding of the geometric properties that make this happen. One of the factors that cause this effect is the fact that the two slightly misaligned sheets interfere with each other to produce larger-grained moiré patterns, which have long been familiar to people in diverse fields such as visual artists, fabric makers and photographers.
In the case of graphene, the natural orientation of the six-carbon hexagons in the single-layer sheets is mimicked and amplified to far larger scales by the moiré effect. This creates very large similarly oriented hexagonal areas called superlattices, which are outlined in blue in the figure. These superlattices consist of very large numbers of atoms in which electron interactions take place, especially at specific twist angles between the two layers. The answers to our puzzle questions below can give you a feel for how similar grids interfere, how the moiré effect amplifies their base patterns, and how certain twist angles may give more interesting results than others.
Problem 1
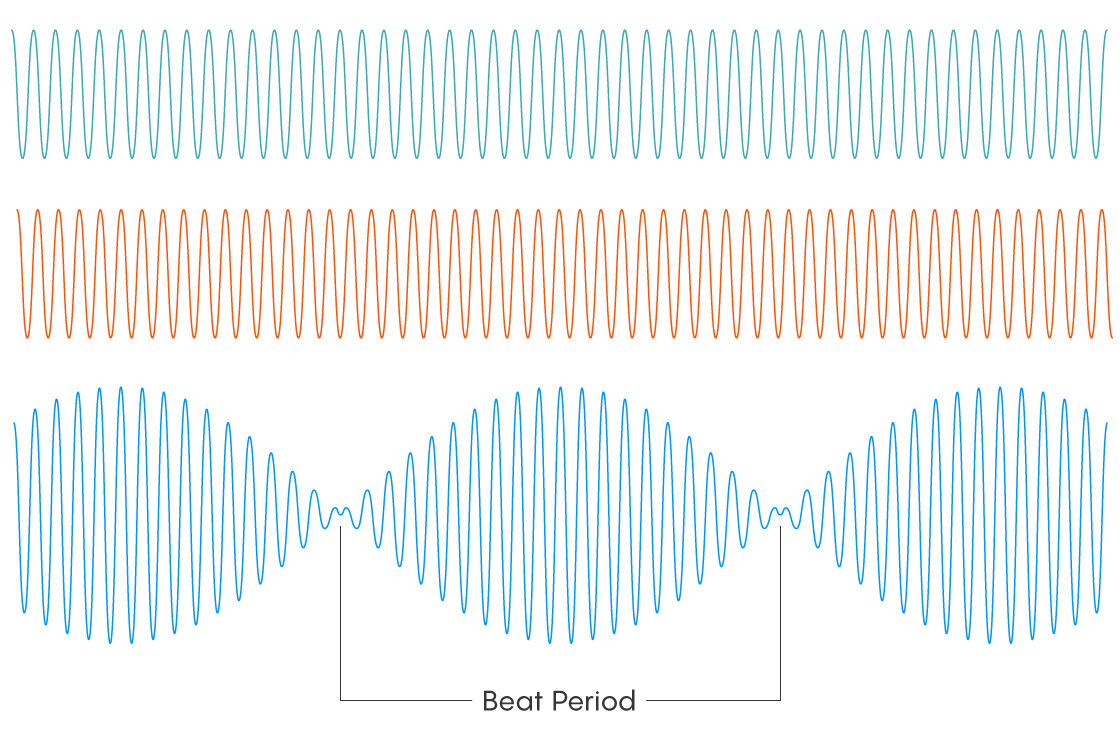
This problem started with the simplest example of how two similar patterns interfere with each other — the phenomenon of acoustic beats. Here, the two interfering patterns are sound waves (mathematically, sine waves) of slightly different frequencies, which together produce the acoustically dominant recurring beat pattern at a frequency that is the difference between the two original frequencies.
5W Infographics for Quanta Magazine
As seen in the figure, the waxing and waning of the beats is caused by the fact that the original sine waves are in phase in the middle of the beat, which makes them reinforce each other, and out of phase between the beats, which makes them cancel each other out. We asked readers to fill in a table, showing what happens when the two frequencies, centered around 500 hertz, converge. The completed table, correctly solved by Douglas Felix, is shown below.
| Beats/sec | Frequency 1 (Hz) | Frequency 2 (Hz) | Beat period (sec) | Oscillations per beat |
| 10 | 505 | 495 | 0.1 | 50 |
| 8 | 504 | 496 | 0.125 | 62.5 |
| 6 | 503 | 497 | 0.167 | 83.3 |
| 4 | 502 | 498 | 0.25 | 125 |
| 2 | 501 | 499 | 0.5 | 250 |
The number of beats per second is equal to the difference in the two frequencies: bps = f1 − f2. The average of the two frequencies is 500, so their sum is 1,000 (f1 + f2 = 1,000). Solving these two equations gives the second and third columns — the frequencies are half the number of beats per second on either side of 500. The beat period is simply the reciprocal of the beats per second, and you can get the oscillations per beat by dividing the base frequency, 500, by the beats per second (opb = 500/bps) or by multiplying the beat period by 500.
Notice how much the beat period increases with just a slight decrease in the frequency difference. When you bring the two frequencies just 1 hertz closer (a 0.2% change from 502 to 501 for f1 and from 498 to 499 for f2), the beat lasts twice as long (a 100% increase). This illustrates that the smaller the difference in the two initial patterns, the larger the grain of the resulting interference pattern.
Problem 2
For this problem, we moved from beats to line moiré patterns.
Assume that the distance from the center of one dark line to the next in the square on the upper right is 10 units. What is the distance between the centers of the dark areas in the moiré pattern if the corresponding distance between lines in the lower left square is a) 12 units or b) 11 units?
As Sanjay pointed out, this is the same as a vernier scale. Exactly! At the center of any dark area of the moiré pattern the dark lines of the two squares are perfectly aligned. Think of this as a coordinate of zero in the vertical direction. From this point, the separation between the dark lines of the two squares initially increases, then decreases, and finally becomes zero at the center of the next dark area. For integer separations the next alignment will happen, as Sanjay pointed out, at the lowest common multiple (LCM) of the two distances. For part a) the answer is the LCM of 10 and 12, which is 60 units; for part b) it’s the LCM of 10 and 11, which is 110 units. Douglas Felix also obtained the right answer, introducing the important concept of the wave number.
Once again a smaller difference between the interfering patterns produces a larger grain in the resulting moiré pattern.
Problem 3
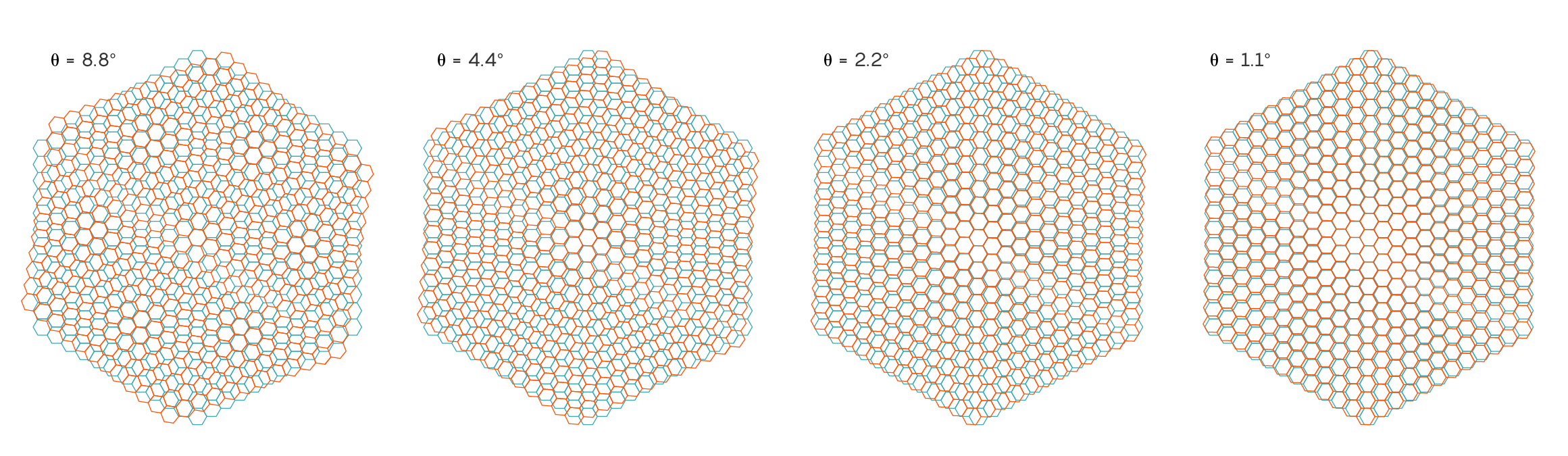
In this problem, we turned our attention to rotated grids of hexagonal cells which reproduce the structure of graphene. As shown in the figure below, the resultant superlattice moiré hexagons double in size at each step as the rotation angle is sequentially halved from 8.8 to 4.4 to 2.2 to 1.1 degrees:
5W Infographics for Quanta Magazine
We asked the following question: When you halve the angle from 2.2 to 1.1 degrees, the angle that produces the interesting effects in graphene, the superlattice seems to have disappeared completely and the pattern looks almost like a single sheet without any moiré. Or does it? What do you think has happened to the large moiré superlattice at this angle? What happens when you halve the angle again a few more times to match some of the even smaller angle predictions?
Milo Hyde nailed the answer as follows:
The depicted 1.1-degree hexagonal lattice is too small to see the moiré pattern. By examining the 8.8-degree lattice, we can infer how large the 1.1-degree lattice needs to be to look identical to the others. Counting from the center hexagon, each depicted lattice consists of 11 rings of hexagons. Therefore, to make the 1.1-degree 11-ring lattice look like the 8.8-degree lattice, we would need to expand the depicted 1.1-degree lattice to 88 rings. To make it look like the 4.4-degree lattice, we would need to expand it to 44 rings, and lastly, to make it look like the 2.2-degree lattice, we would need to expand it to 22 rings.
If we halve the angle from 1.1-degrees, the corresponding lattice needs to double in size to see the moiré pattern, i.e., a 0.55-degree lattice would need to be expanded to 176 rings to look like the depicted 11-ring 8.8-degree lattice. This doubling continues indefinitely.
Problem 4
In this problem we tackled the mystery of graphene’s “magic angles.” The graphene moiré patterns change in a smooth and continuous manner as the angle of rotation of the second sheet decreases. The superlattice hexagons get smaller and more numerous, and their size varies continuously with the angle. However, the electron tunneling phenomenon is discrete and recurs periodically at specific angles only. Can you venture an entirely geometric explanation of how the seemingly continuous rotation profile could possibly produce a discrete physical phenomenon that only recurs periodically?
Once again, I liked Milo Hyde’s answer, which describes an almost perfect physical analogy:
Similar to how blowing air across an open bottle produces a fundamental resonant tone plus higher harmonics, the electron tunneling phenomenon resonates (fundamentally) starting at a 1.1-degree graphene rotation angle and then periodically reoccurs at higher “harmonic” angles. It is important to note that in the physical analogy, the excitation — blowing air across the bottle opening — is a continuous, broadband excitation similar to the continuous graphene rotation angle. In the bottle analogy, the fundamental resonant tone is related to 1/(L/2), where L is the length of the bottle. I hypothesize something similar shows up when one solves Schrodinger’s equation, a wave equation, with the applicable boundary conditions describing the rotated graphene geometry.
As these slides describe, the distance between the centers of two adjacent hexagons apparently needs to be about 13 nanometers (which it is at 1.1 degrees of rotation) or a simple fraction thereof.
Now that we’ve dealt with our puzzle problems, it’s time for the poetry! We asked you to come up with your best verses to explain the graphene story while parodying the famous song “That’s Amore.”
My brother Madhav privately sent me this eminently singable one:
When a grid’s misaligned, with a like one behind, that’s a Moiré.
This seems like a fitting beginning to a very good one contributed by Ty Rex:
When the twist is just right
Then electrons take flight —
That’s a moiré —
And coherently gel
Into super-sized cells —
That’s a moiré.
Thank you, Ty Rex. Your final lines were good, but they didn’t adhere to the parody template, so I didn’t include them. Perhaps readers can find a fitting ending and we can have our own crowd-sourced “Graphene a Moiré” anthem!
Thank you, everyone, for contributing. I must commend Sanjay for his answer to problem 2, and especially Douglas Felix for answering all the problems correctly. Douglas Felix is a veteran to this column and has twice won the Insights prize. This time, the prize goes to Milo Hyde for his answers to the last two problems.
See you next month for new Insights.