Did the Chicken Come First or Is It Turtles All the Way Down?

When you consider the origin of life, the origin of the universe, or any other origin story, one question inevitably rears its ugly head: What caused the beginning? This apparent paradox has vexed humanity for millennia. It’s responsible for philosophical terms like “the prime or unmoved mover” or “the uncaused cause,” and for the postulation of innumerable gods and deities in religious circles. It’s also responsible for catchphrases that suggest impossibility, such as “It’s a chicken-and-egg problem” or the whimsical “It’s turtles all the way down!” In spite of it all, science has achieved considerable insight on this question of infinite regress. This month, we examine the conundrum with the help of some questions and puzzles. Some require serious thought or investigation, and others are more whimsical and subjective, but hopefully all will be illuminating.

In biology, the problem of infinite regress has been solved by Darwin’s theory of evolution, a feat so momentous that the philosopher Daniel Dennett has called it “the single best idea anyone ever had.” Darwin’s theory of evolution explained the origins of biology as “descent with modification” that takes place by means of the ingenious principle of natural selection — Darwin adduced mountains of evidence for both the process and the mechanism. From a philosophical perspective, Darwin’s solution has a couple of features that neatly melt the conceptual difficulties we have with infinite regress. The first is the notion that the categories we think of as fixed, such as species, are in fact fluid, slowly and imperceptibly evolving from one into another over the ages. The second is the idea that as we go backward in time, life-forms get simpler and simpler, with transitional forms bridging the gaps we see between modern species. The forms at the very beginning are so simple that it becomes easier to see them arising from nothing more than elementary physics and chemistry, as has been shown by experiments in which mixtures of chemical elements placed in primitive conditions produce the building blocks of life.

Let’s get a feel for these ideas with a couple of questions.

Question 1

Take a look at the change in facial features between our apelike ancestors and modern humans in this video rendition by the “paleoartist” John Gurche, in which 7 million years of evolutionary history are compressed into less than three minutes. At what point in the video would it no longer surprise you to see the depicted face in a gathering of humans in a modern city? Assuming that the video has a linear timescale, how long ago would that be?

If beings with the intermediate facial characteristics shown in this video were present on Earth today, the artificiality of the separation between apes and humans would be more visually obvious. The second point I mentioned about evolution, the gradual progression from the simplest creatures almost 4 billion years ago to the complex organisms of today, can also be seen in other time-lapse videos (such as this one).

Question 2

Next, let’s delve deeper into evolutionary biology to tackle the chicken-and-egg problem and dispel its implied impossibility. As with the first question, the problem only seems intractable because of the false implication that chickens were always chickens and eggs were always eggs. Let’s clarify the meaning of these categories in four different ways. In each of the questions below you have to specify which of the two came first and approximately how many years ago this happened.

1. Define “chicken” as the bird we would recognize today, and “egg” as the specific kind that would give rise to that bird. Which came first and how long ago?
2. Define “chicken” as the bird we would recognize today, and “egg” as something similar in size and shape to one we would use in an omelet. Which came first and how long ago?
3. At some point in the evolutionary process, something emerged in the history of life called the alternation of generations. Organisms started existing in two alternating forms: One was the complex metabolizing organism (an animal or plant), and the second was a dormant entity such as an egg, seed or spore that would give rise to it. Define “chicken” as the first type and “egg” as the second type. Which came first and how long ago?
4. When life first emerged, even the simplest forms had two components that coexisted — the biochemistry or set of chemical reactions it needed to metabolize and live, and the DNA or RNA or other code that could generate the organism from scratch, given the proper environment. Define “chicken” as the first part and “egg” as the second part. Which came first and how long ago?

Now let’s turn to physics, in which the problem of infinite regress is deeper. Here it remains unsolved and perhaps always will. This seems unavoidable, because as we dig deeper into the structure and origin of the universe there will invariably come a point where no further progress can be made, at least for a time, and there is no way to know if we have reached rock bottom or if there is still another turtle to discover. Let’s look at what we’ve found already.

We can start with the question that led the ancients to posit a prime mover: How did motion start? The most firmly established modern explanation for the origin of the universe is the Big Bang, a cosmic explosion that occurred approximately 13.8 billion years ago in a featureless high-density, high-temperature singularity. Following this, a process of evolution occurred that’s analogous to the one in biology. The fundamental forces were established and elementary particles, atoms, stars and chemical elements were formed, more or less following the laws we know today. In this scenario, motion hardly needs an explanation — it seems to be the natural order of things. Everything is in motion relative to something else. What’s impossible is a total lack of motion — perfect rest. It is because the ancients imagined creation arising out of nothingness that they needed a prime mover.

As in biology, this explanation satisfies the requirement that the initial state be simple, without the complexity and variety that we currently see. But what caused the Big Bang? We don’t really know, but based on extrapolation from phenomena that we do know, the best answer we can give is “a gigantic quantum fluctuation.” Is this rock bottom, or is there something that can explain how the laws governing the universe came into existence? We do know something about that. In 1918, Emmy Noether proved a famous theorem showing that symmetry is responsible for conservation laws. And in a recent Quanta article, “Why the Laws of Physics Are Inevitable,” Natalie Wolchover describes the “bootstrap approach,” which assumes that the laws of nature essentially dictate one another through their mutual consistency — that nature “pulls itself up by its own bootstraps.” Thus, it has been proved that the existence of spin-2 particles invariably gives rise to the equivalence principle and general relativity. Of course, understanding all this requires specialized training in mathematics and physics, but here is a whimsical situation in a toy universe that shows how the properties of a hypothetical particle can influence the laws of the universe.

Puzzle 1

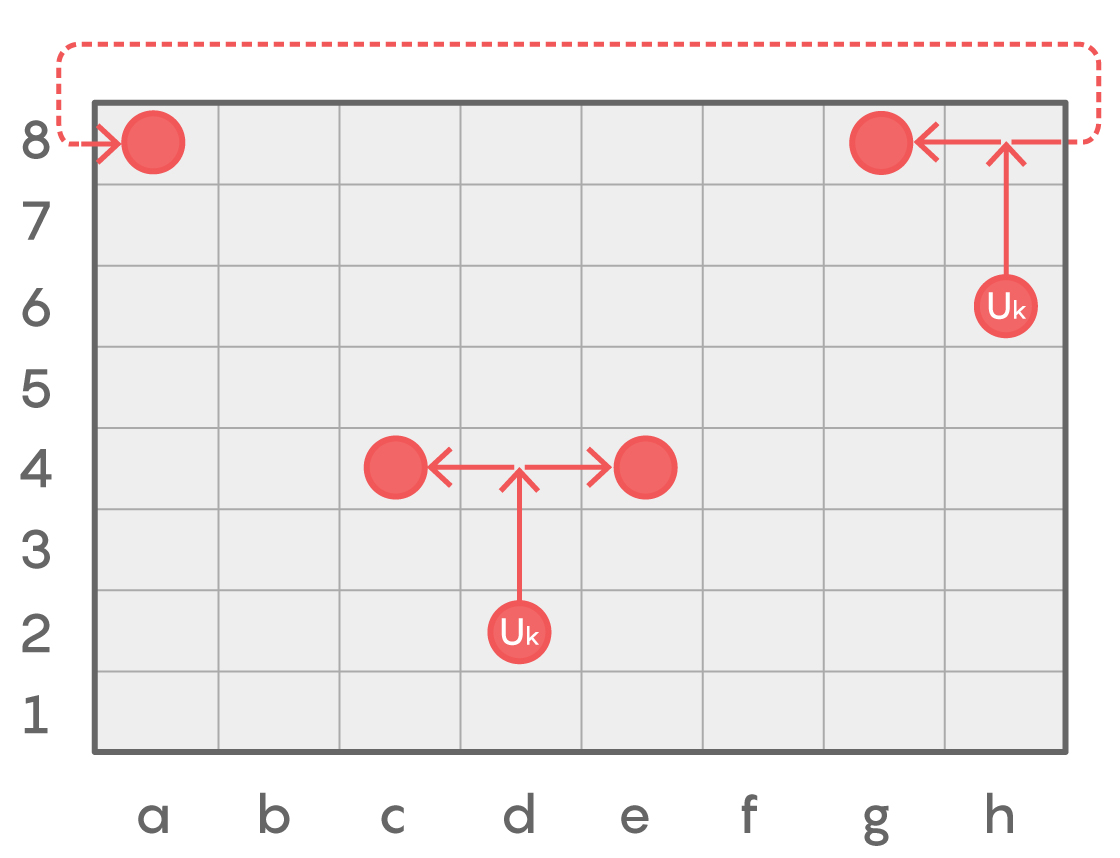
Imagine a two-dimensional universe divided into an 8-by-8 grid as shown below. This universe has a particle called a U_k (short for “upward knight”). The U_k can make a quantum jump to a square two squares above and one square to the left or right. Thus a U_k at d2 can move to c4 (up-left jump) or e4 (up-right jump), but not to any other square on this jump. If the U_k is in a position like h6, such that its up-right quantum jump will take it outside the universe’s grid, the particle will leave the universe on the right side and reappear via a wormhole on the left side at a8 in the position that it would have reached in the hypothetical grid of the adjacent parallel universe. From a8, an up-right jump takes it to b2, while an up-left jump will take it to h2, after a double wormhole ride. Two U_ks that can reach the same square are said to be the same color. Based on the symmetry properties of the U_k’s jumps, how many colors does this universe have?

So it may be possible to derive the laws of our universe based on considerations of symmetry and consistency. The physicist Paul Dirac conjectured more than 80 years ago that the laws in our universe and the values of physical constants may evolve with time. The cosmologist Lee Smolin carried the biological analogy even further, speculating that inside black holes, universes may give rise to baby universes, each with slightly different laws and constants from its parent. These baby universes would persist longer if the mutated laws made them more stable, in a process of cosmological natural selection. It turns out that a universe with parameters optimized for maximizing fecund black holes also produces the right conditions to support life. Thus, Smolin’s cosmological natural selection might account for the anthropic principle, the idea that cosmological theories of the universe must necessarily allow for human existence.

Let’s consider the origin of one more property of our universe — its quantum randomness (indeterminacy), which we discussed a few months ago. A deterministic algorithm cannot produce inherent randomness; it can only produce pseudo-randomness. However, a complex nonlinear interaction of multiple particles — deterministic chaos, as happens with the weather — can be indistinguishable from indeterminacy. Could the underlying cause of quantum indeterminacy be deterministic chaos at some much smaller subquantum scale? After all, a bunch of pennies (or M&M’s) shaken in a box can simulate the radioactive decay of atoms, a process that is supposed to be inherently random and unpredictable in quantum mechanics.

The deterministic chaos induced by shaking pennies in a box is a result of many objects interacting with forces that operate haphazardly in multiple directions. As you decrease the complexity of the situation or algorithm, the results get less random. Simple linear pseudo-random number generators that iteratively obtain sequences of random numbers in computers have gotten pretty good, but the earliest ones often failed pattern detection tests. Our last puzzle challenges you to make one of them perform better.

Puzzle 2

One of the first simple methods of generating pseudo-random numbers, the middle square method, was invented by the mathematician John von Neumann in 1949. You take a numeric seed with an even number of digits (say four), square it, and extract the middle four digits, which become the next seed. For example, if 7,478 is the seed, squaring it gives you 55,920,484, yielding the four digits 9,204, which become the next seed. If the square has fewer than eight digits, you add leading zeros.

The problem with this method is that if the middle four digits of the square are all zeros, the generator will then output only zeros. Also, the generator can get stuck in short repeating cycles for some other seed numbers. It is generally found that only about 60% of all possible four-digit numbers can be generated by this method. Can you tweak the middle square method by adding one or two additional rules that use simple substitution or arithmetic operations on one or more digits in order to generate a greater proportion of four-digit numbers? For example, you can make a rule that a zero in a certain position will be replaced with a 5, or that you subtract 2 if the last digit is greater than 5, or something similar that might improve this random number generator.

(Updated on Feb. 7, 2020: Cornflower has pointed out that it might be possible to use the tweaks to generate a greater proportion of four-digit numbers without improving the quality of the random number generator. Hence, please aim your tweaks to try and increase the length of the longest cycle of four-digit numbers that the middle square method can generate, before a previous number is repeated.)

In addition to solving these puzzles, please give your own views on the thorny topic of infinite regress. Happy puzzling!

Editor’s note: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt or one of the two Quanta books, Alice and Bob Meet the Wall of Fire or The Prime Number Conspiracy (winner’s choice). And if you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION.” (It will not appear online, so solutions to the puzzle above should be submitted separately.)

Note that we may hold comments for the first day or two to allow for independent contributions by readers.

Update: The solution has been published here.