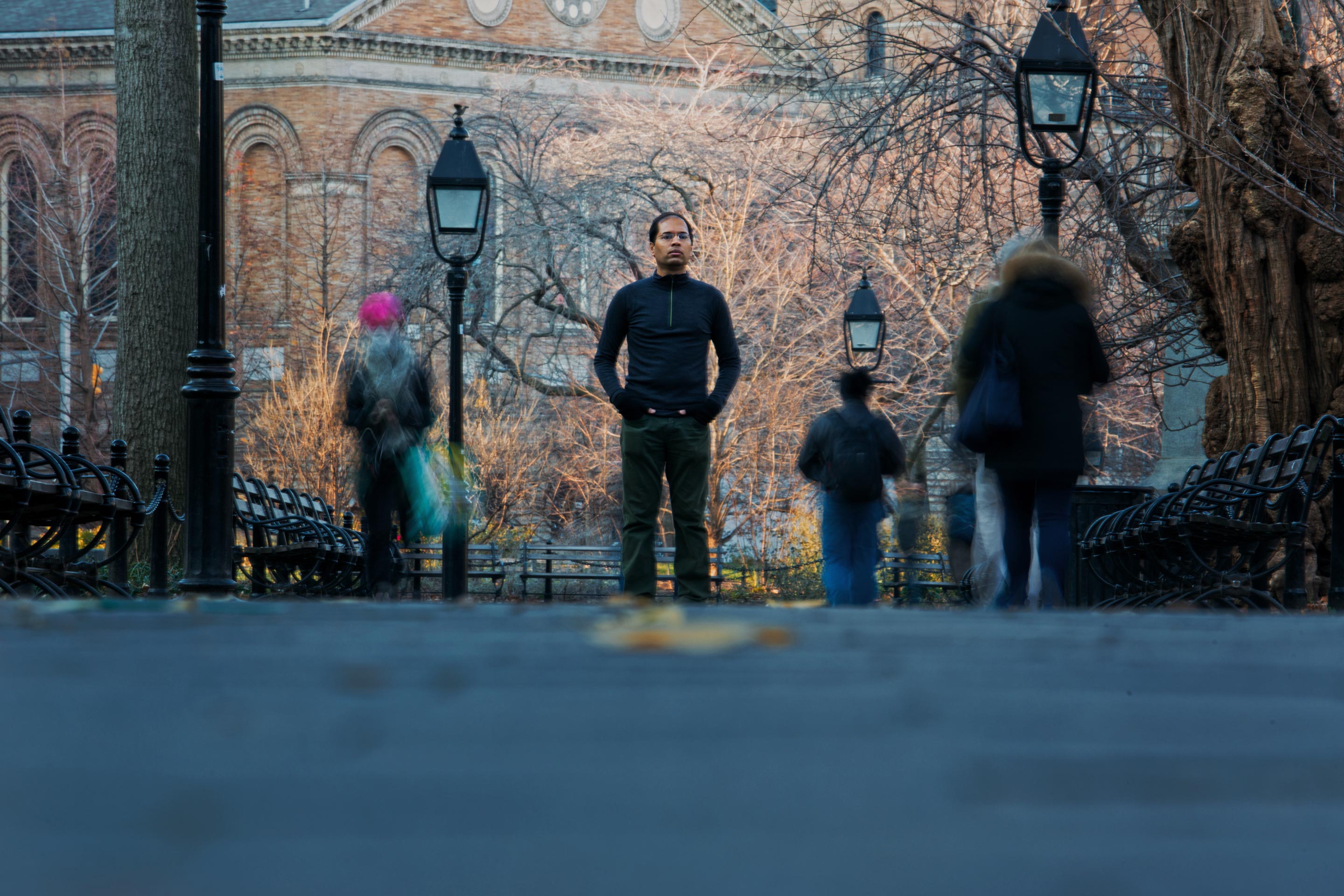
Subhash Khot’s favorite place to think about computational complexity is Washington Square Park in New York City.
Béatrice de Géa for Quanta Magazine
Introduction
As a Princeton University graduate student in 2001, Subhash Khot was visiting his family in India and thinking about his research on the limits of computation when he came up with a good, if seemingly modest, idea. He was thinking about an analytic theorem that Johan Håstad, one of his mentors, had formulated (and Jean Bourgain had proved) and how it could be applied to the “hardness of approximation.” But there was a missing ingredient.
While most computer scientists work to expand the capabilities of computers, computational complexity experts like Khot try to determine which problems are impossible for computers to solve within a reasonable time frame. Once a problem has been classified as “hard” in this way, the natural next question to ask is about its hardness of approximation: whether a computer can efficiently find an approximate solution good enough to put to practical use.
In thinking about the analytic theorem and these hardness questions, Khot realized that the missing ingredient was an existing problem called Unique Games. “I posited that the problem is indeed computationally hard, which became the Unique Games Conjecture,” Khot told Quanta in an email. He found that assuming that the Unique Games problem was hard made it much easier to show that another problem he was working on was also hard.
“I was happy of course and I told my family that I had an idea that was worth pursuing,” said Khot. “I certainly did not think that it would have such a wide range of applications.” After returning to Princeton, he was surprised to discover that his assumption worked for several of his other problems too. It seemed like a useful idea, and he wrote a paper that appeared the following spring.
In his paper, Khot found connections between his conjecture and an important hardness of approximation paper by Irit Dinur and Shmuel Safra, which fueled excitement in the field. “I think I was at the right place at the right time,” Khot said. In the following years, the connections extended to other big problems, further elevating the conjecture’s profile and influence. In 2014, Khot, who is now a professor at New York University’s Courant Institute of Mathematical Sciences, was awarded the Rolf Nevanlinna Prize, one of the top honors in theoretical computer science.



Khot chalked on the pavement in Washington Square Park some of the key ideas from an approach he’s developing with Irit Dinur, Guy Kindler, Dor Minzer and Shmuel Safra for proving the Unique Games Conjecture.
Béatrice de Géa for Quanta Magazine
As a theorist, Khot is able to work anywhere — with his relatives in India, in bustling New York City cafes, even in movie theaters. But his favorite thinking place is Washington Square Park, just across the street from his NYU office and the faculty apartment where he lives with his wife and son. “My work is mainly thinking and for the most part, I am stuck and not making progress,” he said. “If I were in the office, I would just get bored and doze off.”
But in the park, “there are entertainers, chess players, fortune tellers, sunbathers, children, tourists, co-existing with squirrels, pigeons, pets and even a hawk that has made this neighborhood his home for several years,” Khot said. “I can stare at all this, listen to all the buzz and keep thinking all day!” The proximity to work, home and nearby restaurants and cafes allows him to work, do his chores, get coffee and look after his son. During the day, he plants himself on one of the shaded benches near the playground, but in the evenings he prefers a scenic spot near the water fountain.
For all the excitement surrounding Khot’s conjecture, the question of whether his assumption is true remains open. These days, as Khot sits quietly in his favorite thinking place, surrounded by the frenetic energy of the park, he is working on two approaches to prove the Unique Games Conjecture, a task he isn’t certain can be accomplished in his lifetime.
Correction: This article was revised on July 10, 2017, to correctly state when the connections between Khot’s conjecture and the paper by Irit Dinur and Shmuel Safra were found.