Symbolic Mathematics Finally Yields to Neural Networks

By translating symbolic math into tree-like structures, neural networks can finally begin to solve more abstract problems.
Jon Fox for Quanta Magazine
Introduction
More than 70 years ago, researchers at the forefront of artificial intelligence research introduced neural networks as a revolutionary way to think about how the brain works. In the human brain, networks of billions of connected neurons make sense of sensory data, allowing us to learn from experience. Artificial neural networks can also filter huge amounts of data through connected layers to make predictions and recognize patterns, following rules they taught themselves.
By now, people treat neural networks as a kind of AI panacea, capable of solving tech challenges that can be restated as a problem of pattern recognition. They provide natural-sounding language translation. Photo apps use them to recognize and categorize recurrent faces in your collection. And programs driven by neural nets have defeated the world’s best players at games including Go and chess.
However, neural networks have always lagged in one conspicuous area: solving difficult symbolic math problems. These include the hallmarks of calculus courses, like integrals or ordinary differential equations. The hurdles arise from the nature of mathematics itself, which demands precise solutions. Neural nets instead tend to excel at probability. They learn to recognize patterns — which Spanish translation sounds best, or what your face looks like — and can generate new ones.
The situation changed late last year when Guillaume Lample and François Charton, a pair of computer scientists working in Facebook’s AI research group in Paris, unveiled a successful first approach to solving symbolic math problems with neural networks. Their method didn’t involve number crunching or numerical approximations. Instead, they played to the strengths of neural nets, reframing the math problems in terms of a problem that’s practically solved: language translation.
“We both majored in math and statistics,” said Charton, who studies applications of AI to mathematics. “Math was our original language.”
As a result, Lample and Charton’s program could produce precise solutions to complicated integrals and differential equations — including some that stumped popular math software packages with explicit problem-solving rules built in.


François Charton (top) and Guillaume Lample, computer scientists at Facebook’s AI research group in Paris, came up with a way to translate symbolic math into a form that neural networks can understand.
François Charton (left) and Guillaume Lample, computer scientists at Facebook’s AI research group in Paris, came up with a way to translate symbolic math into a form that neural networks can understand.
Courtesy of Facebook
The new program exploits one of the major advantages of neural networks: They develop their own implicit rules. As a result, “there’s no separation between the rules and the exceptions,” said Jay McClelland, a psychologist at Stanford University who uses neural nets to model how people learn math. In practice, this means that the program didn’t stumble over the hardest integrals. In theory, this kind of approach could derive unconventional “rules” that could make headway on problems that are currently unsolvable, by a person or a machine — mathematical problems like discovering new proofs, or understanding the nature of neural networks themselves.
Not that that’s happened yet, of course. But it’s clear that the team has answered the decades-old question — can AI do symbolic math? — in the affirmative. “Their models are well established. The algorithms are well established. They postulate the problem in a clever way,” said Wojciech Zaremba, co-founder of the AI research group OpenAI.
“They did succeed in coming up with neural networks that could solve problems that were beyond the scope of the rule-following machine system,” McClelland said. “Which is very exciting.”
Teaching a Computer to Speak Math
Computers have always been good at crunching numbers. Computer algebra systems combine dozens or hundreds of algorithms hard-wired with preset instructions. They’re typically strict rule followers designed to perform a specific operation but unable to accommodate exceptions. For many symbolic problems, they produce numerical solutions that are close enough for engineering and physics applications.
Neural nets are different. They don’t have hard-wired rules. Instead, they train on large data sets — the larger the better — and use statistics to make very good approximations. In the process, they learn what produces the best outcomes. Language translation programs particularly shine: Instead of translating word by word, they translate phrases in the context of the whole text. The Facebook researchers saw that as an advantage to solving symbolic math problems, not a hindrance. It gives the program a kind of problem-solving freedom.
That freedom is especially useful for certain open-ended problems, like integration. There’s an old saying among mathematicians: “Differentiation is mechanics; integration is art.” It means that in order to find the derivative of a function, you only have to follow some well-defined steps. But to find an integral often requires something else, something that’s closer to intuition than calculation.
The Facebook group suspected that this intuition could be approximated using pattern recognition. “Integration is one of the most pattern recognition-like problems in math,” Charton said. So even though the neural net may not understand what functions do or what variables mean, they do develop a kind of instinct. The neural net begins to sense what works, even without knowing why.
For example, a mathematician asked to integrate an expression like $latex y y^{\prime}\left(y^{2}+1\right)^{-1 / 2}$ will intuitively suspect that the primitive — that is, the expression that was differentiated to give rise to the integral — contains something that looks like the square root of y² + 1.
To allow a neural net to process the symbols like a mathematician, Charton and Lample began by translating mathematical expressions into more useful forms. They ended up reinterpreting them as trees — a format similar in spirit to a diagrammed sentence. Mathematical operators such as addition, subtraction, multiplication and division became junctions on the tree. So did operations like raising to a power, or trigonometric functions. The arguments (variables and numbers) became leaves. The tree structure, with very few exceptions, captured the way operations can be nested inside longer expressions.
“When we see a large function, we can see that it’s composed of smaller functions and have some intuition about what the solution can be,” Lample said. “We think the model tries to find clues in the symbols about what the solution can be.” He said this process parallels how people solve integrals — and really all math problems — by reducing them to recognizable sub-problems they’ve solved before.
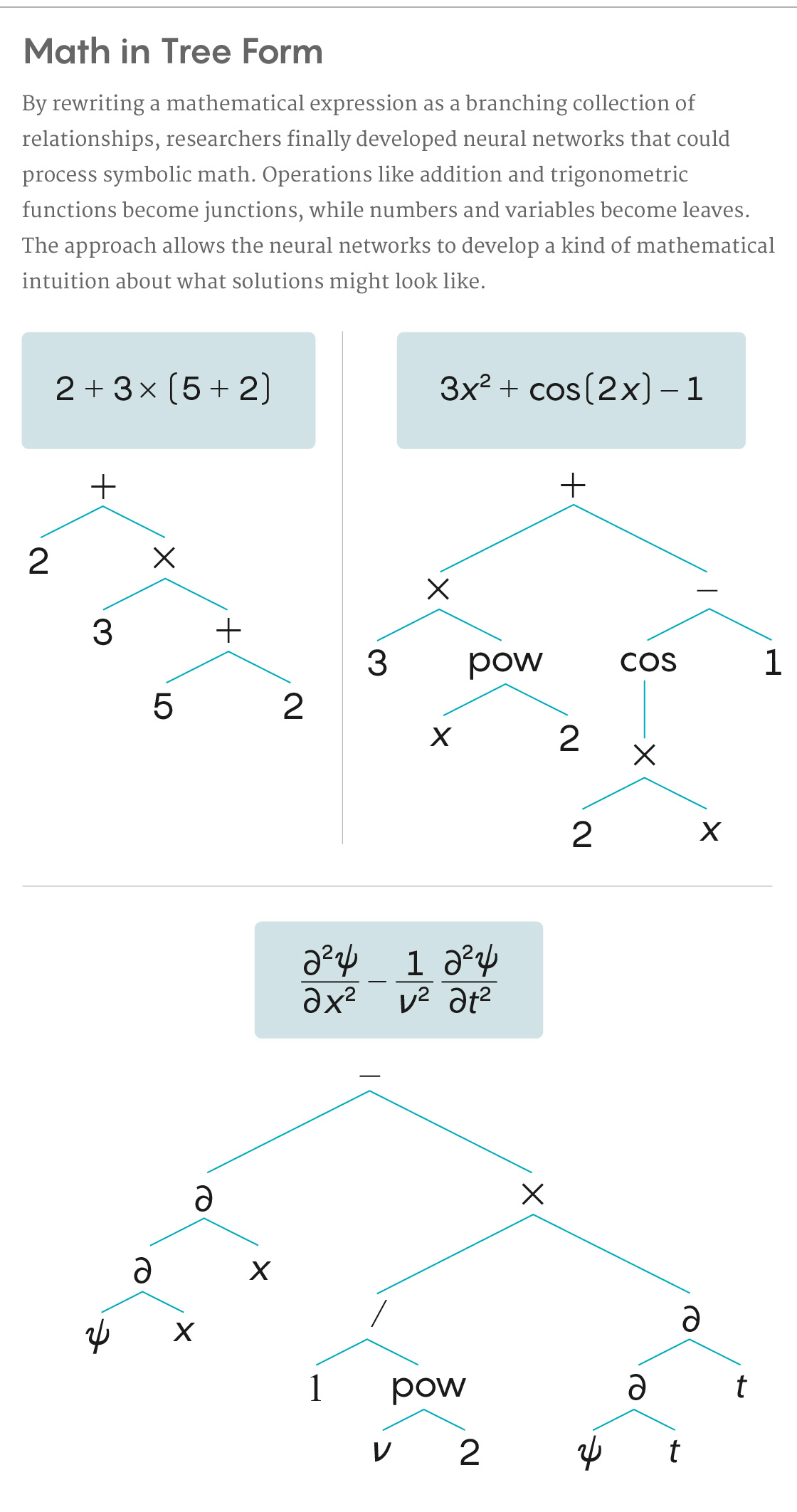
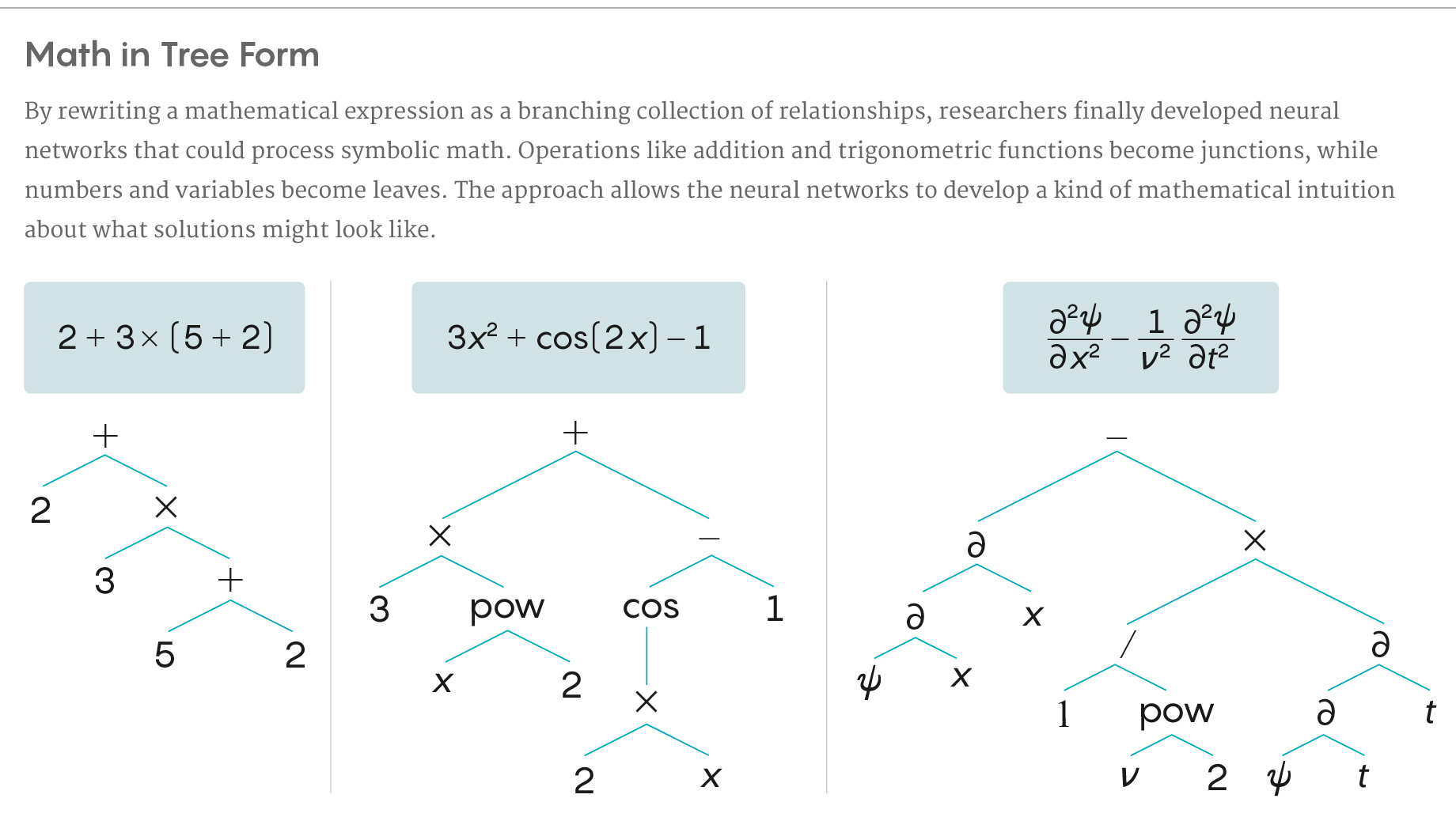
5W Infographics for Quanta Magazine
After coming up with this architecture, the researchers used a bank of elementary functions to generate several training data sets totaling about 200 million (tree-shaped) equations and solutions. They then “fed” that data to the neural network, so it could learn what solutions to these problems look like.
After the training, it was time to see what the net could do. The computer scientists gave it a test set of 5,000 equations, this time without the answers. (None of these test problems were classified as “unsolvable.”) The neural net passed with flying colors: It managed to get the right solutions — precision and all — to the vast majority of problems. It particularly excelled at integration, solving nearly 100% of the test problems, but it was slightly less successful at ordinary differential equations.
For almost all the problems, the program took less than 1 second to generate correct solutions. And on the integration problems, it outperformed some solvers in the popular software packages Mathematica and Matlab in terms of speed and accuracy. The Facebook team reported that the neural net produced solutions to problems that neither of those commercial solvers could tackle.
Into the Black Box
Despite the results, the mathematician Roger Germundsson, who heads research and development at Wolfram, which makes Mathematica, took issue with the direct comparison. The Facebook researchers compared their method to only a few of Mathematica’s functions —“integrate” for integrals and “DSolve” for differential equations — but Mathematica users can access hundreds of other solving tools.
Germundsson also noted that despite the enormous size of the training data set, it only included equations with one variable, and only those based on elementary functions. “It was a thin slice of possible expressions,” he said. The neural net wasn’t tested on messier functions often used in physics and finance, like error functions or Bessel functions. (The Facebook group said it could be, in future versions, with very simple modifications.)
And Frédéric Gibou, a mathematician at the University of California, Santa Barbara who has investigated ways to use neural nets to solve partial differential equations, wasn’t convinced that the Facebook group’s neural net was infallible. “You need to be confident that it’s going to work all the time, and not just on some chosen problems,” he said, “and that’s not the case here.” Other critics have noted that the Facebook group’s neural net doesn’t really understand the math; it’s more of an exceptional guesser.
Still, they agree that the new approach will prove useful. Germundsson and Gibou believe neural nets will have a seat at the table for next-generation symbolic math solvers — it will just be a big table. “I think that it will be one of many tools,” Germundsson said.
Besides solving this specific problem of symbolic math, the Facebook group’s work is an encouraging proof of principle and of the power of this kind of approach. “Mathematicians will in general be very impressed if these techniques allow them to solve problems that people could not solve before,” said Anders Hansen, a mathematician at the University of Cambridge.
Another possible direction for the neural net to explore is the development of automated theorem generators. Mathematicians are increasingly investigating ways to use AI to generate new theorems and proofs, though “the state of the art has not made a lot of progress,” Lample said. “It’s something we’re looking at.”
Charton describes at least two ways their approach could move AI theorem finders forward. First, it could act as a kind of mathematician’s assistant, offering assistance on existing problems by identifying patterns in known conjectures. Second, the machine could generate a list of potentially provable results that mathematicians have missed. “We believe that if you can do integration, you should be able to do proving,” he said.
Offering assistance for proofs may ultimately be the killer app, even beyond what the Facebook team described. One common way to disprove a theorem is to come up with a counterexample that shows it can’t hold. And that’s a task that these kinds of neural nets may one day be uniquely suited for: finding an unexpected wrench to throw in the machine.
Another unsolved problem where this approach shows promise is one of the most disturbing aspects of neural nets: No one really understands how they work. Training bits enter at one end and prediction bits emerge from the other, but what happens in between — the exact process that makes neural nets into such good guessers — remains a critical open question.
Symbolic math, on the other hand, is decidedly less mysterious. “We know how math works,” said Charton. “By using specific math problems as a test to see where machines succeed and where they fail, we can learn how neural nets work.”
Soon, he and Lample plan to feed mathematical expressions into their networks and trace the way the program responds to small changes in the expressions. Mapping how changes in the input trigger changes in the output might help expose how the neural nets operate.
Zaremba sees that kind of understanding as a potential step toward teaching neural nets to reason and to actually understand the questions they’re answering. “It’s easy in math to move the needle and see how well [the neural network] works if expressions are becoming different. We might truly learn the reasoning, instead of just the answer,” he said. “The results would be quite powerful.”
This article was reprinted on Spektrum.de.



