What's up in
Combinatorics
Latest Articles
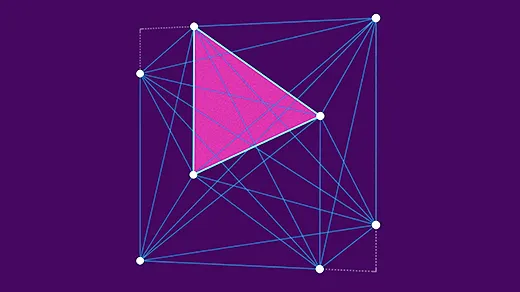
The Biggest Smallest Triangle Just Got Smaller
A new proof breaks a decades-long drought of progress on the problem of estimating the size of triangles created by cramming points into a square.
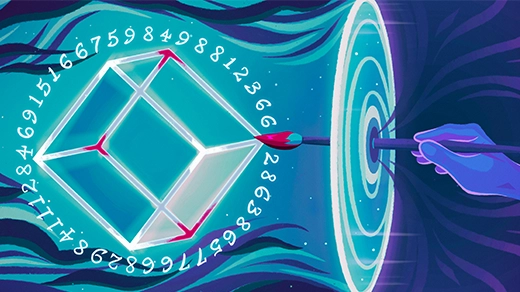
Ninth Dedekind Number Found by Two Independent Groups
The numbers count a variety of seemingly unrelated mathematical structures.
Mathematicians Solve Long-Standing Coloring Problem
A new result shows how much of the plane can be colored by points that are never exactly one unit apart.
The Lawlessness of Large Numbers
Mathematicians can often figure out what happens as quantities grow infinitely large. What about when they are just a little big?
Computer Scientists Inch Closer to Major Algorithmic Goal
A new paper finds a faster method for determining when two mathematical groups are the same.
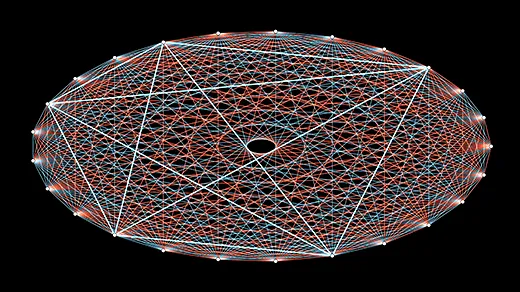
Mathematicians Discover Novel Way to Predict Structure in Graphs
Mathematicians probe the limits of randomness in new work estimating quantities called Ramsey numbers.
First-Year Graduate Student Finds Paradoxical Set
No two pairs have the same sum; add three numbers together, and you can get any whole number.
How Math Has Changed the Shape of Gerrymandering
New tools make it possible to detect hidden manipulation of maps.
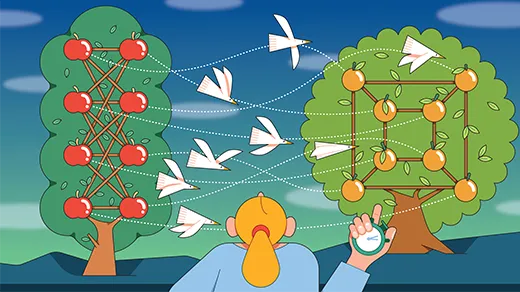
A Very Big Small Leap Forward in Graph Theory
Four mathematicians have found a new upper limit to the “Ramsey number,” a crucial property describing unavoidable structure in graphs.