What's up in
Combinatorics
Latest Articles
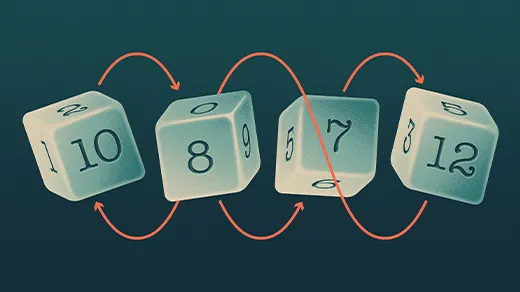
Mathematicians Roll Dice and Get Rock-Paper-Scissors
Mathematicians have uncovered a surprising wealth of rock-paper-scissors-like patterns in randomly chosen dice.
Google Researcher, Long Out of Math, Cracks Devilish Problem About Sets
On nights and weekends, Justin Gilmer attacked an old question in pure math using the tools of information theory.
The Year in Math
Four Fields Medals were awarded for major breakthroughs in geometry, combinatorics, statistical physics and number theory, even as mathematicians continued to wrestle with how computers are changing the discipline.
From Systems in Motion, Infinite Patterns Appear
Mathematicians are finding inevitable structures in sufficiently large sets of integers.
Hypergraphs Reveal Solution to 50-Year-Old Problem
In 1973, Paul Erdős asked if it was possible to assemble sets of “triples” — three points on a graph — so that they abide by two seemingly incompatible rules. A new proof shows it can always be done.
For His Sporting Approach to Math, a Fields Medal
With Hugo Duminil-Copin, thinking rarely happens without moving. His insights into the flow-related properties of complex networks have earned him the Fields Medal.
He Dropped Out to Become a Poet. Now He’s Won a Fields Medal.
June Huh wasn’t interested in mathematics until a chance encounter during his sixth year of college. Now his profound insights connecting combinatorics and geometry have led to math’s highest honor.
In Times of Scarcity, War and Peace, a Ukrainian Finds the Magic in Math
With her homeland mired in war, the sphere-packing number theorist Maryna Viazovska has become the second woman to win a Fields Medal in the award’s 86-year history.
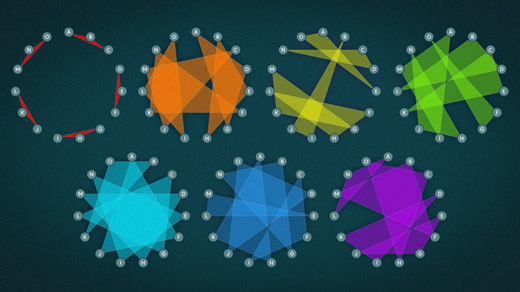
What a Math Party Game Tells Us About Graph Theory
Play this simple math game with your friends to gain insights into fundamental principles of graph theory.