What's up in
Erdős conjecture
Latest Articles
Grad Students Find Inevitable Patterns in Big Sets of Numbers
A new proof marks the first progress in decades on a problem about how order emerges from disorder.
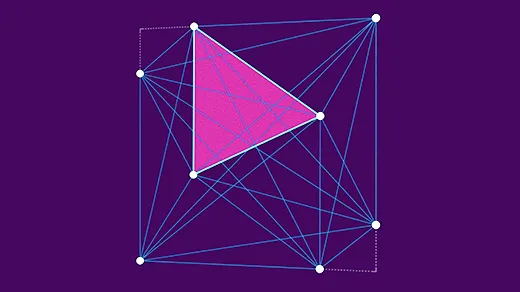
The Biggest Smallest Triangle Just Got Smaller
A new proof breaks a decades-long drought of progress on the problem of estimating the size of triangles created by cramming points into a square.
Mathematicians Solve Long-Standing Coloring Problem
A new result shows how much of the plane can be colored by points that are never exactly one unit apart.
The Lawlessness of Large Numbers
Mathematicians can often figure out what happens as quantities grow infinitely large. What about when they are just a little big?
Mathematicians Discover Novel Way to Predict Structure in Graphs
Mathematicians probe the limits of randomness in new work estimating quantities called Ramsey numbers.
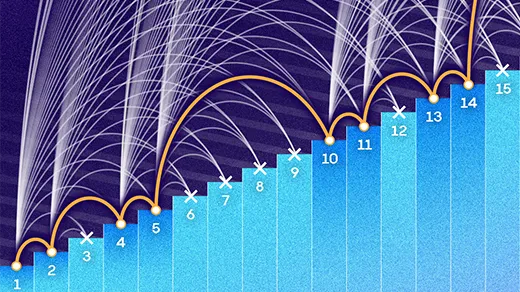
First-Year Graduate Student Finds Paradoxical Set
No two pairs have the same sum; add three numbers together, and you can get any whole number.
A Very Big Small Leap Forward in Graph Theory
Four mathematicians have found a new upper limit to the “Ramsey number,” a crucial property describing unavoidable structure in graphs.
Surprise Computer Science Proof Stuns Mathematicians
For decades, mathematicians have been inching forward on a problem about which sets contain evenly spaced patterns of three numbers. Last month, two computer scientists blew past all of those results.
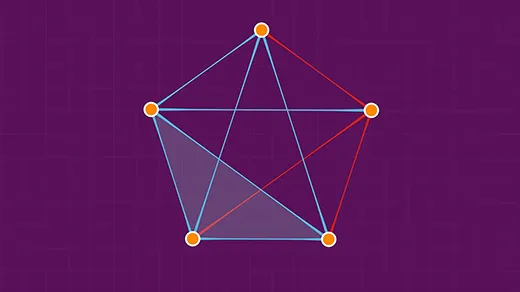
Mathematicians Settle Erdős Coloring Conjecture
Fifty years ago, Paul Erdős and two other mathematicians came up with a graph theory problem that they thought they might solve on the spot. A team of mathematicians has finally settled it.