Teen Mathematicians Tie Knots Through a Mind-Blowing Fractal
Introduction
In the fall of 2021, Malors Espinosa set out to devise a special type of math problem. As with any good research question, it would have to be thought-provoking, its solution nontrivial — something others would want to study. But an additional constraint stumped him. Malors, then a graduate student in mathematics at the University of Toronto, wanted high school students to be able to prove it.
For years, Malors had been running summer workshops for local high schoolers, teaching them about basic ideas in mathematical research and showing them how to write proofs. But a few of his students seemed ready to do more — to find out what it means to do math when there is no answer key. They just needed the right question to guide them.
Malors finally found one while reading a textbook about chaos. In its pages, he came across a familiar object: a fractal, or self-similar shape, called the Menger sponge, which has a simple but elegant construction. First divide a cube into what looks like a Rubik’s cube. Remove the cube in the very center, along with the center cube of each of the six faces. Then repeat this process for each of the 20 remaining cubes. And repeat. And repeat. You’ll quickly see why the resulting fractal is called a sponge: With each iteration, its pores multiply exponentially.
Mark Belan/Quanta Magazine
Ever since Karl Menger introduced his fractal sponge nearly a century ago, it has captured the imaginations of professional and amateur mathematicians alike. One reason: It looks cool. In 2014, hundreds of math enthusiasts participated in a global effort, called MegaMenger, to build finite, 200-pound versions of the sponge out of business cards. Because of its porous, foam-like structure, the sponge has also been used to model shock absorbers and exotic forms of space-time.
But most important, the fractal possesses various counterintuitive mathematical properties. Continue to pluck out ever smaller pieces, and what started off as a cube becomes something else entirely. After infinitely many iterations, the shape’s volume dwindles to zero, while its surface area grows infinitely large. Such is the weirdness of fractals: hovering somewhere between dimensions, occupying space without truly filling it.
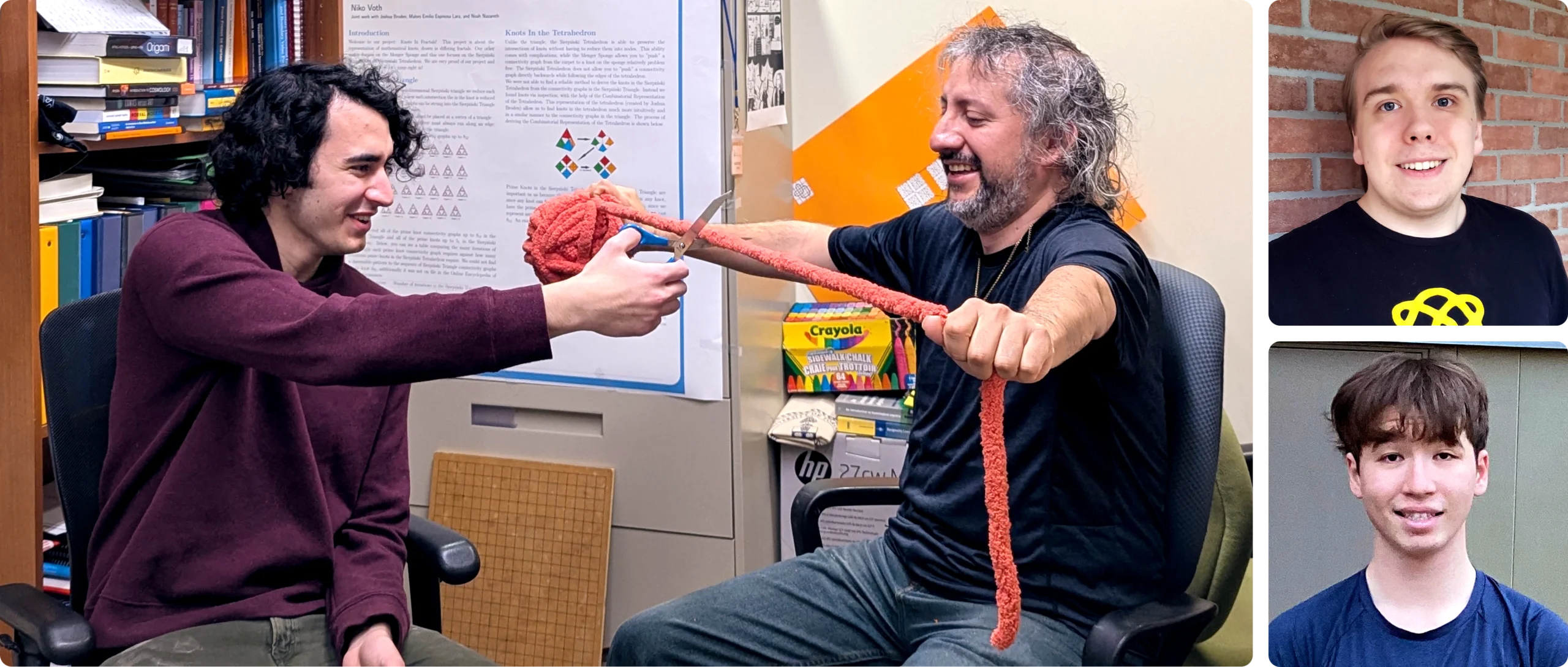
Three high school students — Niko Voth (top right), Joshua Broden (bottom right) and Noah Nazareth (far left) — recently proved a new theorem about knots and fractals with the help of their mentor Malors, a mathematician at the University of Toronto.
Clockwise from left: Somja Injac, Christian Voth and Timur Khayrullin
When he first defined his sponge in 1926, Menger also proved that any conceivable curve — simple lines and circles, structures that look like trees or snowflakes, fractal dusts — can be deformed and then embedded somewhere on the sponge. They can be made to wind their way along the sponge’s convoluted contours without ever leaving its surface, hitting a hole, or intersecting themselves. The sponge, Menger wrote, was therefore a “universal curve.”
But this, Malors later realized, raised a new question. Menger had proved that you could find a circle in his sponge. But what about objects that were equivalent, in a certain sense, to the circle? Consider a mathematical knot: a string that’s been twisted and tied up, its ends then closed to form a loop. From the outside, it might look like a tangled mess. But an ant walking along it would eventually find itself back where it started, just as it would on a circle. In this way, every knot is equivalent, or “homeomorphic,” to a circle.
Every knot is “homeomorphic” to the circle, meaning that it’s possible to map the points from one to the other while satisfying a simple set of conditions.
Menger’s statement didn’t distinguish between homeomorphic curves. His proof only guaranteed, for instance, that the circle could be found in his sponge — not that all homeomorphic knots could be, their loops and tangles still intact. Malors wanted to prove that you could find every knot within the sponge.
It seemed like the right mashup to excite young mathematicians. They’d recently had fun learning about knots in his seminar. And who doesn’t love a fractal? The question was whether the problem would be approachable. “I really hoped there was an answer,” Malors said.
There was. After just a few months of weekly Zoom meetings with Malors, three of his high school students — Joshua Broden, Noah Nazareth and Niko Voth — were able to show that all knots can indeed be found inside the Menger sponge. Moreover, they found that the same can likely be said of another related fractal, too.
“It’s a clever way of putting things together,” said Radmila Sazdanovic, a topologist at North Carolina State University who was not involved in the work. In revisiting Menger’s century-old theorem, she added, Malors — who usually does research in the disparate field of number theory — had apparently asked a question that no one thought to ask before. “This is a very, very original idea,” she said.
A Different Way to See Knots
Broden, Nazareth and Voth had taken several of Malors’ summer workshops over the years. When he first taught them about knots in an earlier workshop, “it blew 14-year-old me’s mind,” said Voth.
But the Menger problem would be their first time moving beyond school workbooks with answer keys. “It was a little bit nerve-racking, because it was the first time I was doing something where truly nobody has the answer, not even Malors,” said Nazareth. Maybe there was no answer at all.
Their goal was essentially to thread a microscopic sewing needle through a cloud of dust — the material that remained of the sponge after many removals. They would have to stick the pin in the right places, tie the knotted tangles with immaculate precision, and never leave the sponge. If their thread ended up floating in the empty holes of the sponge for any knot, it was game over.
Not an easy task. But there was a way to simplify it. Knots can be depicted on a flat piece of paper as special diagrams called arc presentations. To create one, you start with information about how the strands of your knot pass in front of or behind each other. Then you apply a set of rules to translate this information into a series of points on a grid. Every row and column of the grid will contain exactly two points.
Connect these points with horizontal and vertical lines. Any time two segments cross paths, draw the vertical one in front of the horizontal one.
Every knot can be represented in this gridlike way. Even though an arc presentation can sometimes look more complicated than other ways of drawing the knot, it makes it easier for mathematicians to study some of the knot’s most important properties.
When the students considered the diagrams of crisscrossing lines, they were reminded of the faces of the Menger sponge. It would be straightforward enough to place the horizontal lines of an arc presentation on one face of the sponge and the vertical lines on its opposite face. The difficulty would be in figuring out how to connect the knot — how to stretch it back into three dimensions. At every one of the arc presentation’s corners, the two faces would need to be connected through the interior of the sponge without accidentally hitting a hole.
To make sure that this was always possible, the mathematicians turned to what’s known as the Cantor set, a one-dimensional analog of the Menger sponge. To construct the set, start with a line segment and divide it into thirds. Remove the middle third, then do the same to the remaining two segments, and so on, ad infinitum. You’ll be left with a scattering of points.
The team considered both a Menger sponge and a Cantor set that have undergone the same number of removal steps. At points on the sponge’s faces whose coordinates are both in the Cantor set, they realized, there shouldn’t be a hole. What’s more, there shouldn’t be holes anywhere directly behind those points either, thanks to the sponge’s repetitive design. A knot would therefore be free and clear to pass through without accidentally jumping off the material of the sponge.
All that was left, then, was for the students to show that they could always compress or stretch a given knot’s arc presentation so that all of its corners would line up with coordinates in the Cantor set. (Such compressing and stretching was allowed because it wouldn’t affect the arc presentation’s overall structure and, therefore, what knot it represents.)
To complete this final step, Broden, Nazareth and Voth took a shortcut. They proved that they could deform any arc presentation so that the points where its vertical and horizontal segments crossed were in the Cantor set. This automatically guaranteed that the larger number of corners would line up with the Cantor set, too. In other words, they could always embed a given knot in some iteration of the Menger sponge.
Now that they’d answered Malors’ original question, they wanted to push their result further. They’d already started to investigate whether all knots could also be embedded in a tetrahedral version of the Menger sponge:
“It was surprisingly annoying,” Broden said. Without the convenience of faces aligned directly opposite one another, their method for pushing knots through the fractal would no longer work.
Measured by Knots
It was at this stage, according to Malors, that the students learned the pain of math research — that a large part of the discipline involves struggling with the failure of a promising avenue of attack. “We’re facing math, and math has no mercy,” he said. “With math as presented to high schoolers, they’re usually protected from that.”
Malors, for his part, was convinced that a so-called trefoil knot couldn’t be found in the tetrahedron. During a Zoom call, the three students pushed back. They left the meeting, they recalled, feeling dispirited and frustrated. But they decided to stick to their instincts. A couple weeks later, to Malors’ surprise, they returned with a result: They had figured out a new way to map the trefoil knot’s arc presentation into the tetrahedron. They later proved that this could be done for all “pretzel” knots, the more general class of knots that the trefoil belongs to — although the question remains open for other kinds of knots.
Malors conjectures that the students’ methods might offer a way to measure the complexity of fractals more broadly. Not all fractals are guaranteed to admit all kinds of knots. Perhaps their structure can be better understood based on what types of knots they can and cannot hold.
At the very least, the work could inspire new art, akin to the 2014 MegaMenger contest. “It would be lovely to see this constructed out of physical materials,” said Allison Moore, a knot theorist at Virginia Commonwealth University.
In the meantime, Broden, Nazareth and Voth have all graduated high school. Only Broden has decided to continue working on the tetrahedron problem — when he’s not busy with college coursework — but all three are considering math careers. “It feels meaningful that I’m trying to contribute to something bigger than myself, to the nature of truth,” Nazareth said. It all starts with asking the right question.



