The Cartoon Picture of Magnets That Has Transformed Science
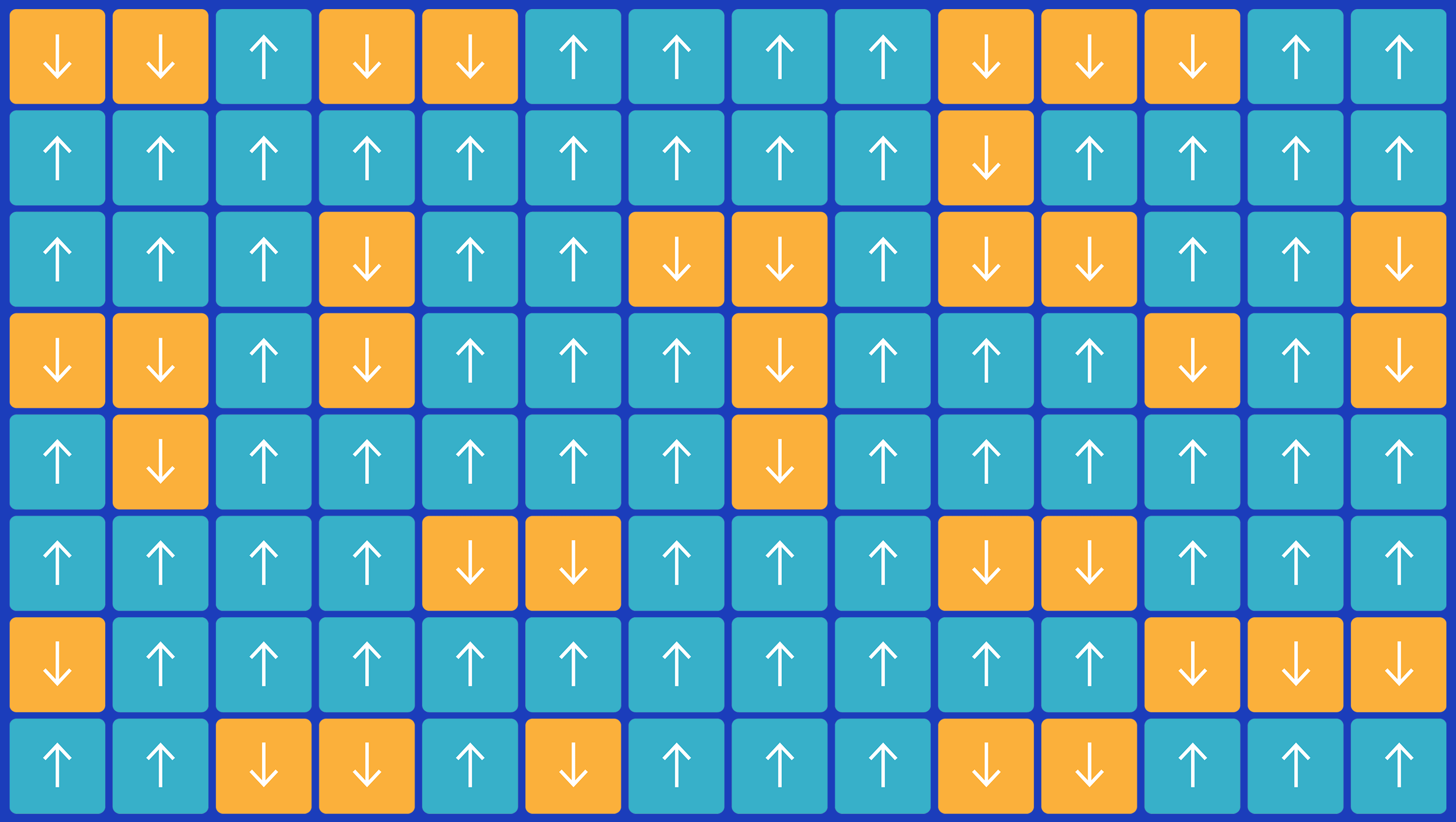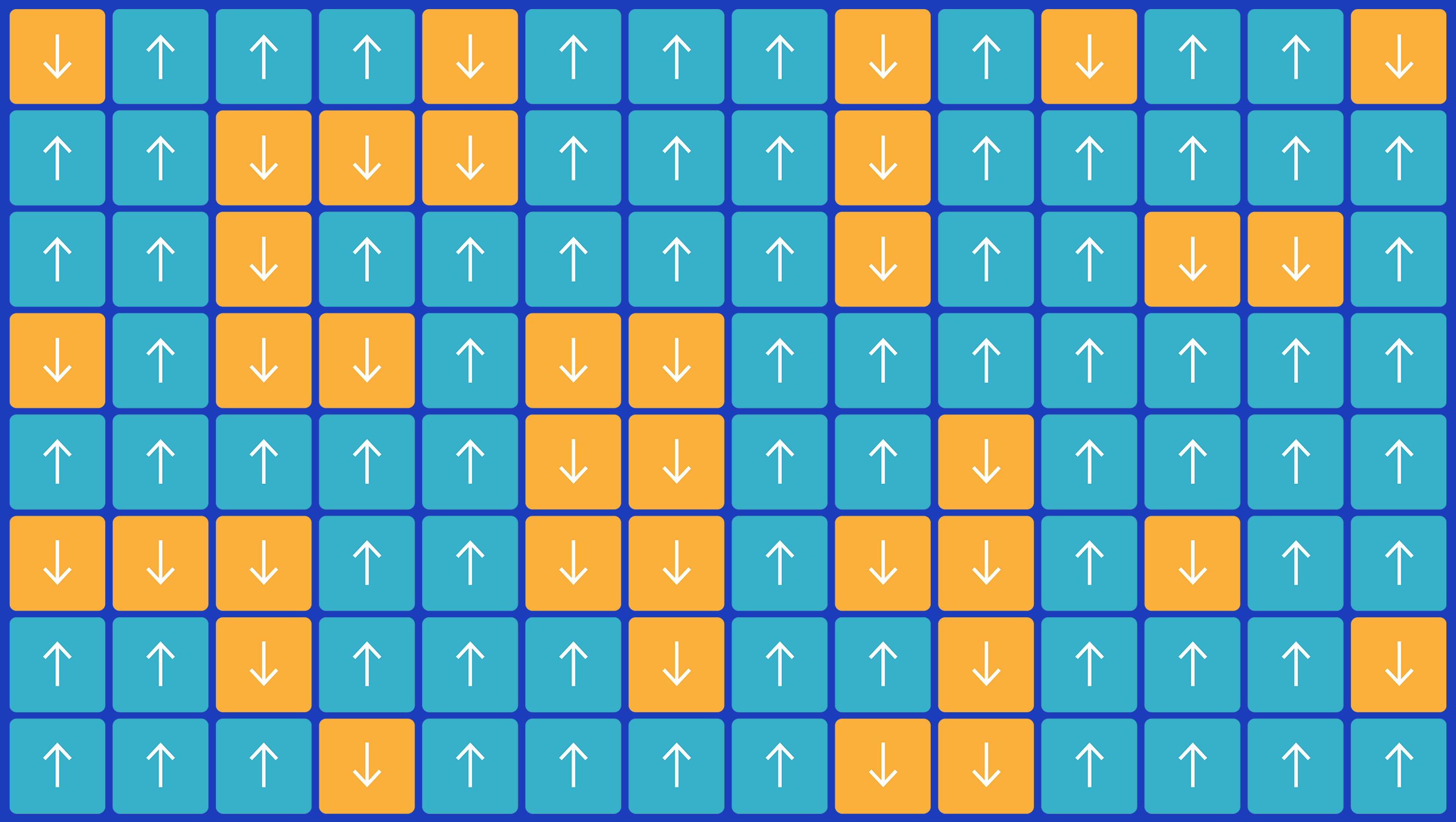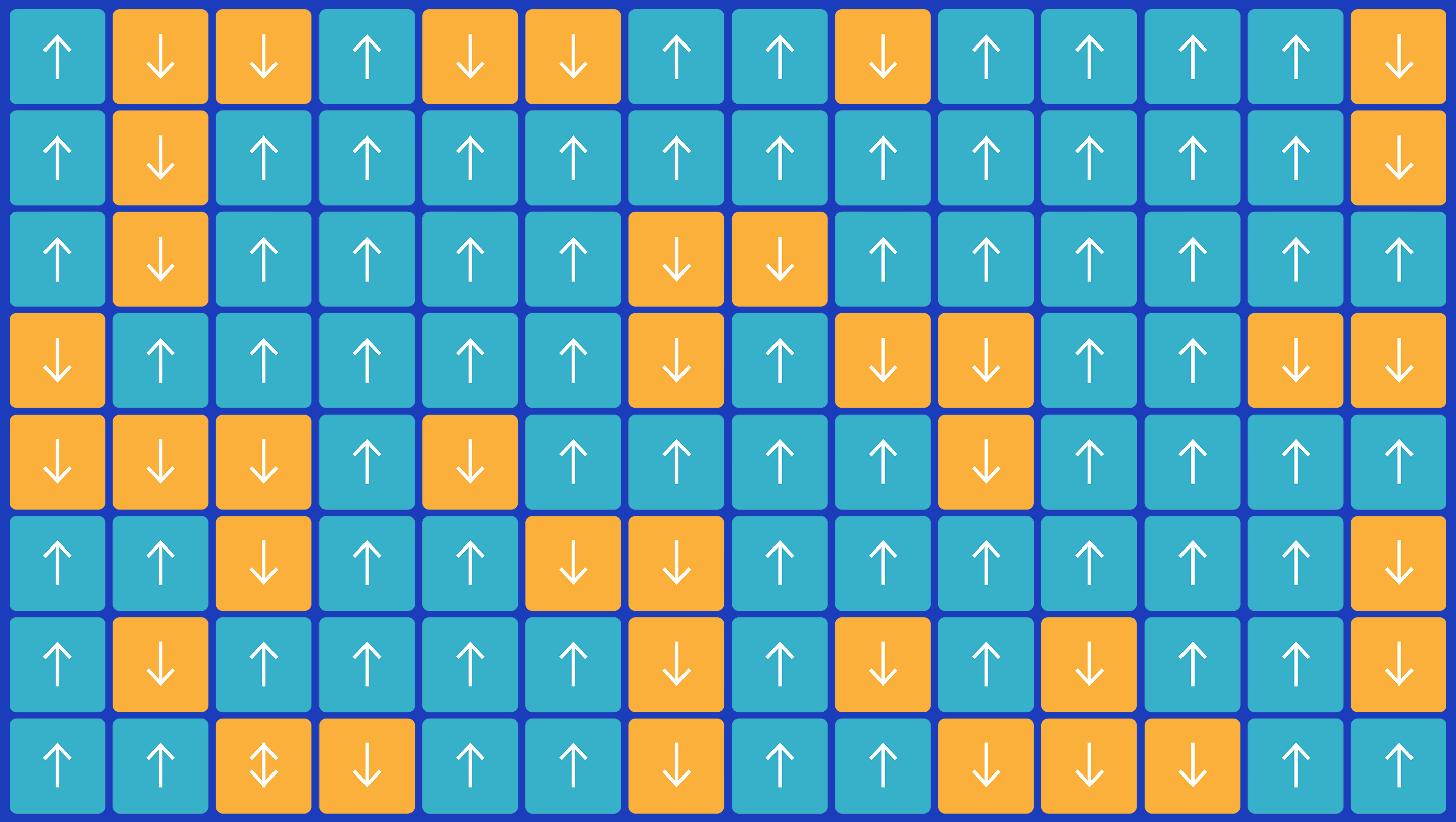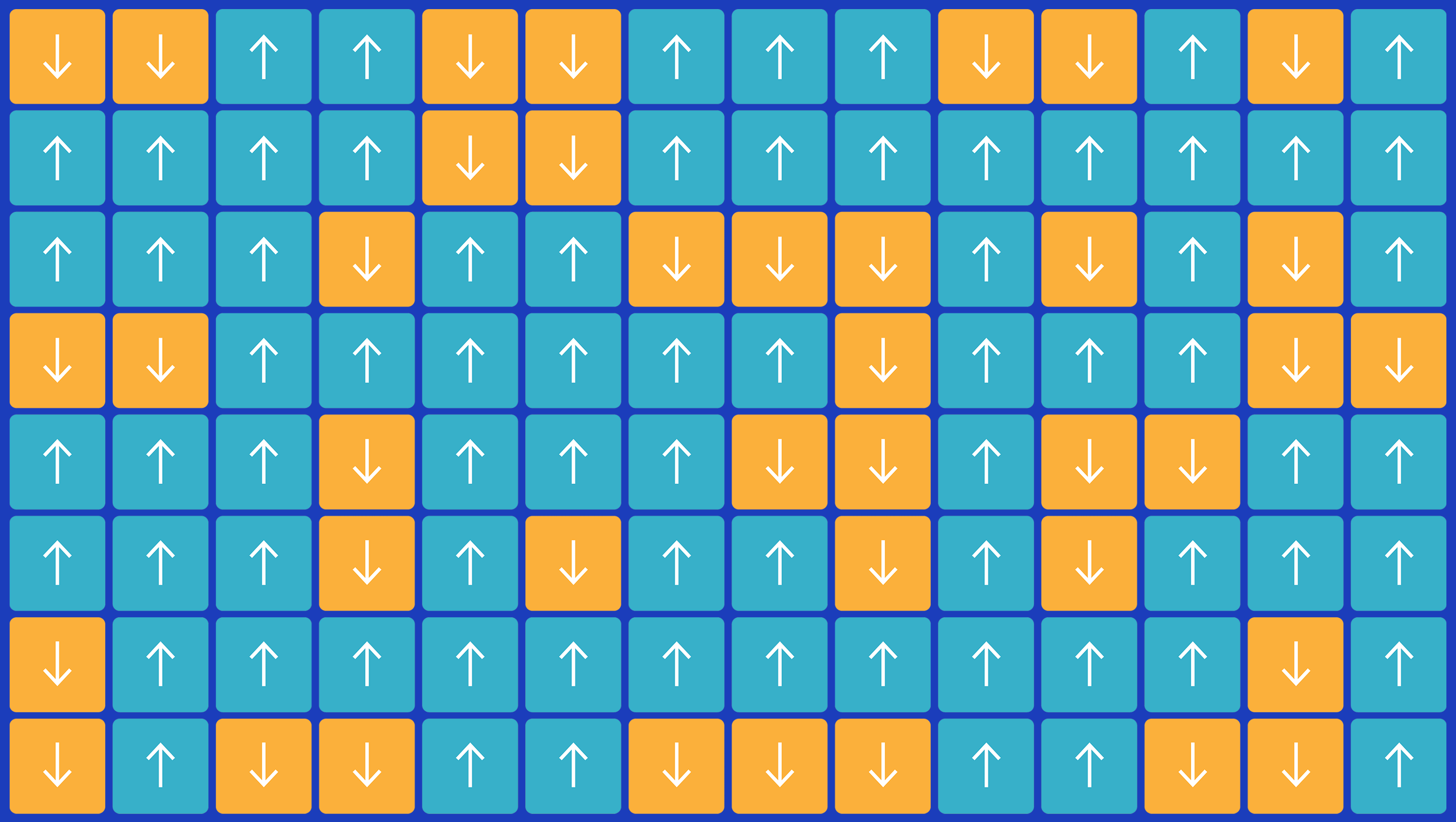
In the Ising model, heat causes arrows to randomly flip while magnetic attraction causes neighbors to align. The struggle captures a huge variety of real-world systems.
Samuel Velasco/Quanta Magazine
Introduction
Sudden, radical transformations of substances known to humanity for eons, like water freezing and soup steaming over a fire, remained mysterious until well into the 20th century. Scientists observed that substances typically change gradually: Heat a collection of atoms a little, and it expands a little. But nudge a material past a critical point, and it becomes something else entirely.
The mathematical key to cracking “phase transitions” debuted exactly 100 years ago, and it has transformed the natural sciences. The Ising model, as it’s known, was initially proposed as a cartoon picture of magnets. It’s now so commonly used as a simple model of physical systems that physicists liken it to the fruit fly, biology’s model organism. A recently published textbook deemed the Ising model “the system that can be used to model virtually every interesting thermodynamic phenomenon.”
It has also penetrated far-flung disciplines well beyond physics, serving as a model of earthquakes, proteins, brains — and even racial segregation.
Here’s the story of how a toy model of magnetism demystified phase transitions, became ubiquitous in science and continues to help push the boundaries of knowledge today.
In 1920, in a world recovering from a global flu pandemic, a German physicist named Wilhelm Lenz set out to understand why heating a magnet past a certain temperature causes it to suddenly lose its attractive power, as Pierre Curie had discovered 25 years earlier. Lenz imagined a magnet as a lattice of little arrows, each pointing either up or down, representing atoms. (Atoms are intrinsically magnetic, with north and south poles, and thus can be thought of as having orientations.) Arrows influence their neighbors, attempting to magnetically flip them to match their own orientation.
Lenz noted that if most atoms pointed together, their tiny magnetic fields would fuse, and the material would act like a magnet overall. But if “up” atoms mixed evenly with “down” atoms, they would neutralize, with no large-scale magnetism emerging.
The feature that launched thousands of physics papers was the struggle within the lattice between heat and magnetism. Heat, the random jiggling of particles, fought for disorder; magnetism resisted this chaos. Lenz supposed that at low temperatures, magnetic order should win. With enough heat, however, random jostling would disrupt the atomic cooperation, explaining Curie’s observation that hot magnets lose their mojo.
Lenz tasked his graduate student, Ernst Ising, with working out the details. Though real magnets are three-dimensional, Ising simplified the situation to a linear chain of arrows, each capable of sensing its two nearest neighbors. Through a calculation now standard in undergraduate textbooks, he showed that the chain — now known as the 1D Ising model — fails to stay magnetized. Random flips overwhelm magnetic cohesion at all temperatures. “One dimension just doesn’t have what it takes,” said John Berlinsky, a condensed matter physicist and professor emeritus at McMaster University in Canada.
Ising published his findings in 1925. He and Lenz assumed that the results held for 2D sheets and 3D blocks of arrows as well, and that the model therefore failed to capture the behavior of real magnets. It seemed destined for the graveyard of incorrect physical theories.
Nevertheless, the Ising model survived as a mathematical curiosity. In the 1940s it caught the attention of Lars Onsager, a theoretical physicist and eventual Nobel laureate. Onsager strove to solve the Ising model — that is, to calculate the proportion of atoms likely to point “up” at any given temperature — for the 2D case, where every arrow has not two but four neighbors.
Solving either case involves tabulating the effects of each arrow on every other arrow, since indirect lines of influence emerge from neighbors acting on neighbors ad infinitum. On a plane, these games of telephone grow far more complex than in a line. Onsager’s solution, published in 1944, represented an “inhuman” work of mathematics, according to the computer scientist Sorin Istrail — one that remains largely inscrutable. “You follow line by line and you get nothing at the end of the proof other than that it is correct,” Istrail said.
Onsager’s proof showed that in 2D, just as Lenz had suspected, arrows align and magnetism carries the day at low temperatures, while disorder wins out after the system surpasses a “critical temperature.” A simple grid of interlinked arrows explains phase transitions. There was no need to incorporate the messiness of real particles, as many physicists had supposed.
Still, the model kept accumulating dust. It seemed to simplify too much, offering a caricature of reality. “It was considered fishy,” said Martin Niss, a historian of physics at Roskilde University in Denmark.
That all changed when painstaking measurements of argon and helium showed that Onsager’s solution nailed the “critical exponents” of these substances. These exponents — numbers like 1/8 and 7/4 — describe the speed at which various properties (such as heat capacity) change in the run-up to phase transitions. By 1965, Niss says, most physicists had come around to Lenz and Ising’s arrows, even as they wondered how a physically unrealistic picture could nail such specific details.
The answer lay not with the model but with nature.
The Ising model is powerful because a range of unrelated substances transform with identical critical exponents — a phenomenon now known as universality.
The American physicist Ken Wilson worked out the mathematics of universality in 1971, winning a Nobel Prize for the effort. Wilson showed that, whereas at high temperatures arrows point whichever way they like, as the system cools and approaches its phase transition, magnetic attraction between neighbors creates larger and larger “islands” of order where all arrows point together. Critical exponents describe the details of this process, such as how the biggest islands grow.

When the Ising model is at its critical temperature, it contains “islands” of aligned arrows of all sizes.
At the critical temperature, islands of all sizes coexist, from dots to continents. Here, one arrow can flip another, distant arrow, despite their not being neighbors — an indication that the system’s macroscopic properties have detached from its microscopic details. This detachment is the magic of universality. All systems with the same number of dimensions and the same symmetries go through identical phase transitions, regardless of whether their microscopic parts are iron atoms, water molecules or little arrows.
Universality means that whenever researchers want to understand a situation with many interacting entities that can be described with opposing labels such as “up” and “down” or “present” and “absent,” they’ll probably start with Ising. “There’s a way in which the Ising model is the simplest solvable model,” said Frances Hellman, a condensed matter physicist at the University of California, Berkeley. “And that gets you a long way toward understanding.” Researchers can also extend the model to suit additional physical systems by letting the arrows spin freely in a plane, for instance.
But even as the Ising model transformed physicists’ understanding of materials, researchers hit a wall in their efforts to exactly solve the 3D version — that is, to find a tidy formula for how magnetized a 3D lattice of arrows becomes at any given temperature. Even Richard Feynman failed in his attempt to complete Ising’s original 1920 assignment.
Today, computers can simulate the 3D Ising model and approximate its critical exponents to a reasonable degree of accuracy, so there’s little urgency to find an exact solution. Yet a yearning persists. One collaboration of physicists announced in 2012 that in exploring the space of logically possible physics theories — where each point matches a set of critical exponents — they had located a region containing the exact critical exponents of the 3D Ising model. Since then the group has whittled down the zone further. In December, they applied their approach to explain a puzzling measurement of liquid helium on a 1992 space shuttle flight.
Grinding out additional decimal places of 3D critical exponents is beside the point, said Slava Rychkov, a physicist at the Institut des Hautes Études Scientifiques in France who is involved in the effort. Elsewhere on their map of possible physics theories live Ising extensions, theories of bizarro universes with exotic particles, and perhaps even the elusive quantum theory of gravity in the real universe. The Ising model represents one of the simplest places in this abstract “theory space,” and so serves as a proving ground for developing novel tools for exploring uncharted territory.
If the exact values of its critical exponents can be pinpointed, “it will happen through some completely unknown, completely new way of solving” theories, Rychkov said. “It will be necessarily a revolution.”



