The Jagged, Monstrous Function That Broke Calculus
Introduction
Calculus is a powerful mathematical tool. But for hundreds of years after its invention in the 17th century, it stood on a shaky foundation. Its core concepts were rooted in intuition and informal arguments, rather than precise, formal definitions.
Two schools of thought emerged in response, according to Michael Barany, a historian of math and science at the University of Edinburgh. French mathematicians were by and large content to keep going. They were more concerned with applying calculus to problems in physics — using it to compute the trajectories of planets, for instance, or to study the behavior of electric currents. But by the 19th century, German mathematicians had begun to tear things down. They set out to find counterexamples that would undermine long-held assumptions, and eventually used those counterexamples to put calculus on more stable and durable footing.
One of these mathematicians was Karl Weierstrass. Though he showed an early aptitude for math, his father pressured him to study public finance and administration, with an eye toward joining the Prussian civil service. Bored with his university coursework, Weierstrass is said to have spent most of his time drinking and fencing; in the late 1830s, after failing to get his degree, he became a secondary school teacher, giving lessons in everything from math and physics to penmanship and gymnastics.
Weierstrass didn’t begin his career as a professional mathematician until he was nearly 40. But he would go on to transform the field by introducing a mathematical monster.
The Pillars of Calculus
In 1872, Weierstrass published a function that threatened everything mathematicians thought they understood about calculus. He was met with indifference, anger and fear, particularly from the mathematical giants of the French school of thought. Henri Poincaré condemned Weierstrass’ function as “an outrage against common sense.” Charles Hermite called it a “deplorable evil.”
To understand why Weierstrass’ result was so unnerving, it helps to first understand two of the most fundamental concepts in calculus: continuity and differentiability.
A continuous function is exactly what it sounds like — a function that has no gaps or jumps. You can trace a path from any point on such a function to any other without lifting your pencil.
Calculus is in large part about determining how quickly such continuous functions change. It works, loosely speaking, by approximating a given function with straight, nonvertical lines.
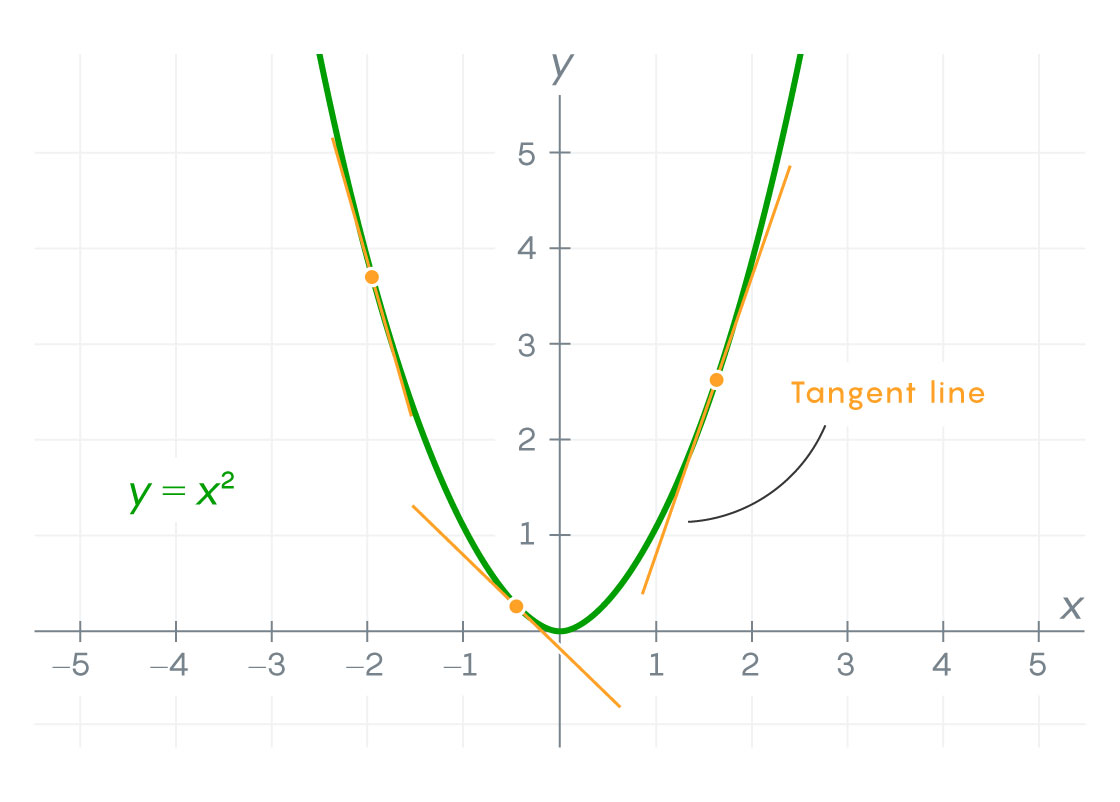
Mark Belan/Quanta Magazine
At any given point on this curve, you can draw a “tangent” line — a line that best approximates the curve near that point. The slope, or steepness, of the tangent line measures how quickly the function is changing at that point. You can define another function, called the derivative, that provides the slope of the tangent line at each point on your original function. If the derivative exists at every point, then the original function is said to be differentiable.
Functions that contain discontinuities are never differentiable: You won’t be able to draw a tangent line that approximates the gaps, meaning your derivative won’t exist there. But even continuous functions aren’t always differentiable at every point. Consider the “absolute value” function, which looks like this:
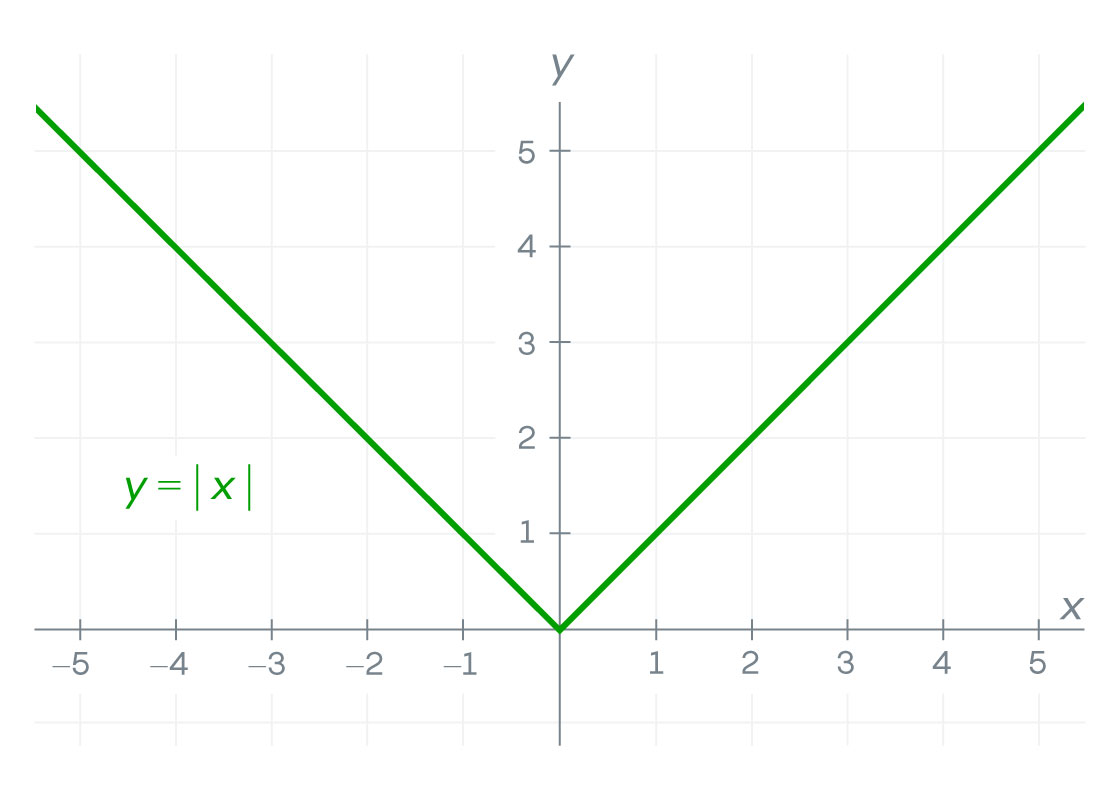
On the left side of this V-shaped curve, tangent lines slope downward. On the right side, they slope upward. At the bottom vertex, the slope abruptly changes directions. The function’s derivative does not exist at that point, even though it’s well defined everywhere else.
This didn’t faze most 19th-century mathematicians. They saw it as an isolated phenomenon: So long as your function is continuous, they claimed, there can only be finitely many points where the derivative is not defined. At all other points, the function should still be nice and smooth. In other words, a function can only zig and zag so much.
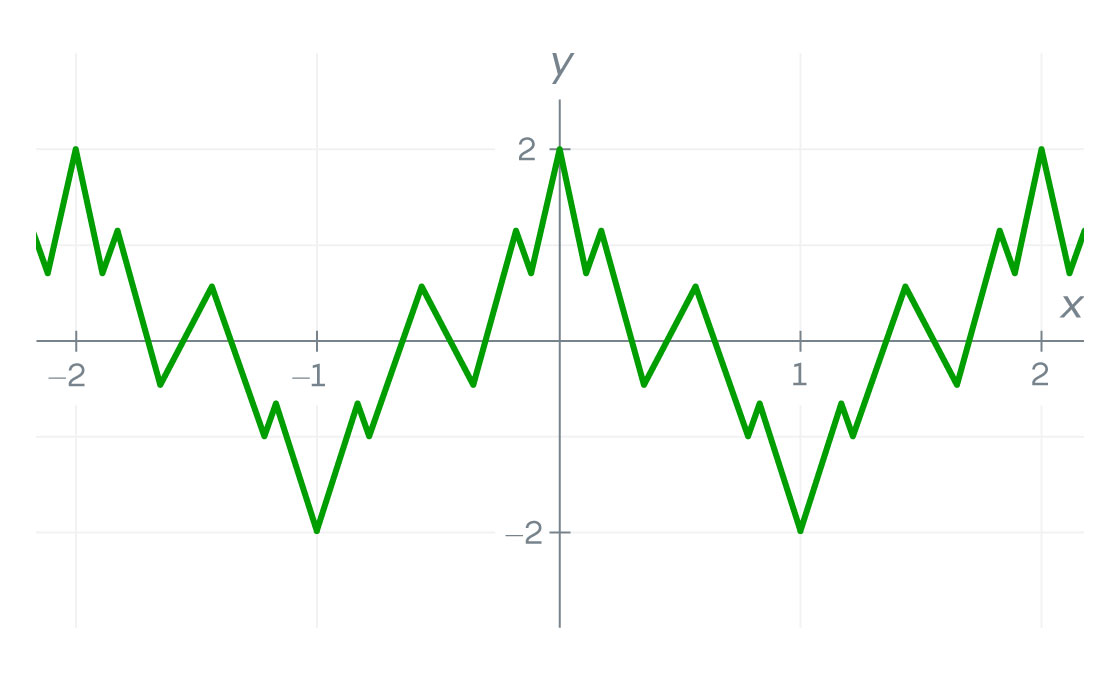
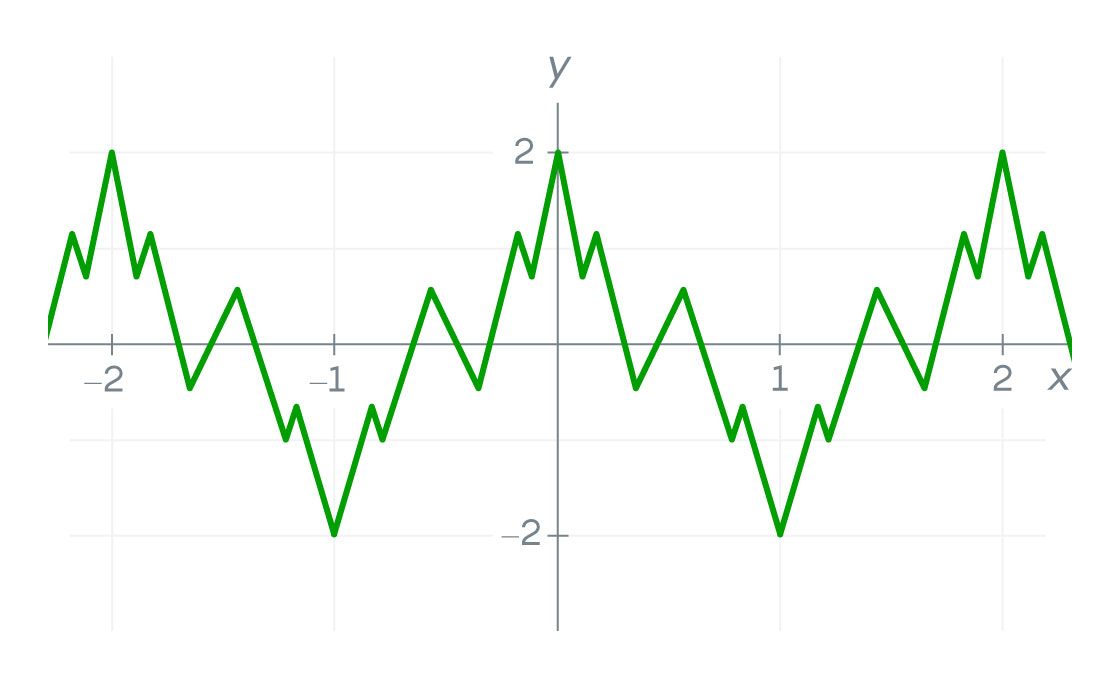
In fact, in 1806, a prominent French mathematician and physicist named André-Marie Ampère claimed that he’d proved this. For decades, his reasoning went unchallenged. Then along came Weierstrass.
Weierstrass’ Monster
Weierstrass discovered a function that, according to Ampère’s proof, should have been impossible: It was continuous everywhere yet differentiable nowhere.
He built it by adding together infinitely many wavelike “cosine” functions. The more terms he added, the more his function zigzagged — until ultimately, it changed direction abruptly at every point, resembling an infinitely jagged sawtooth comb.
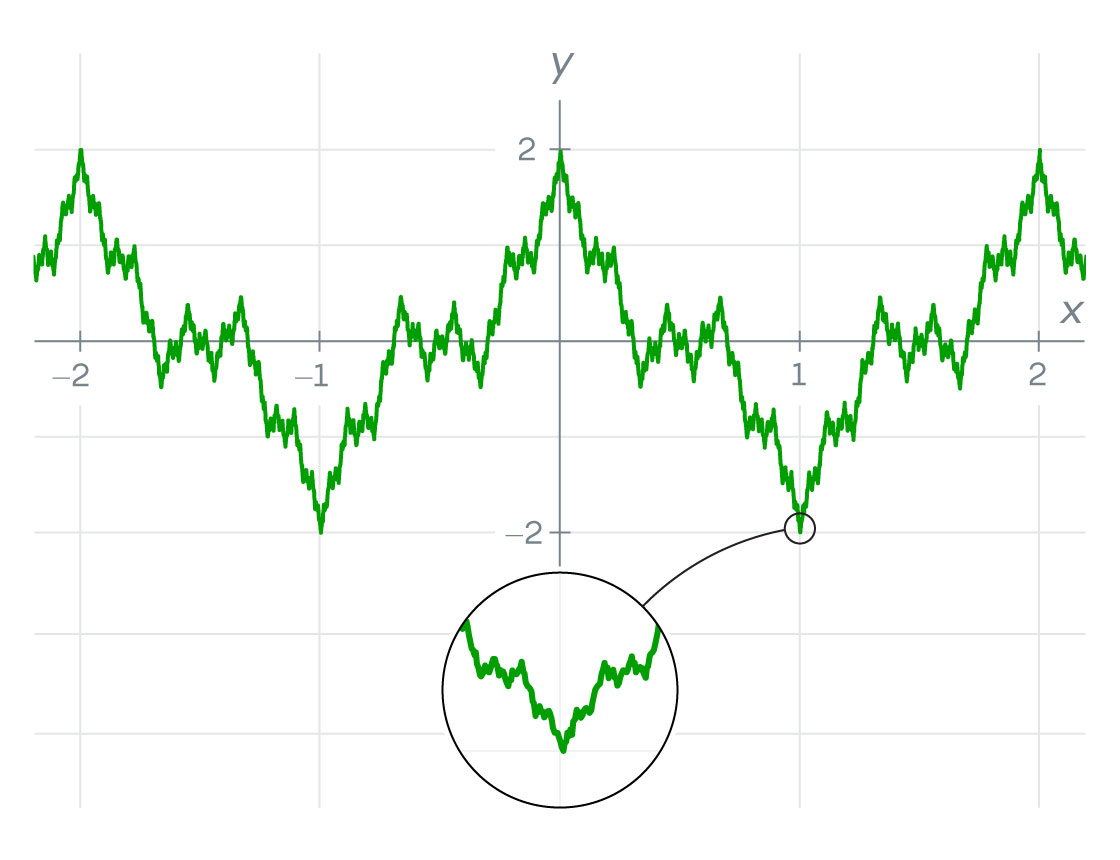
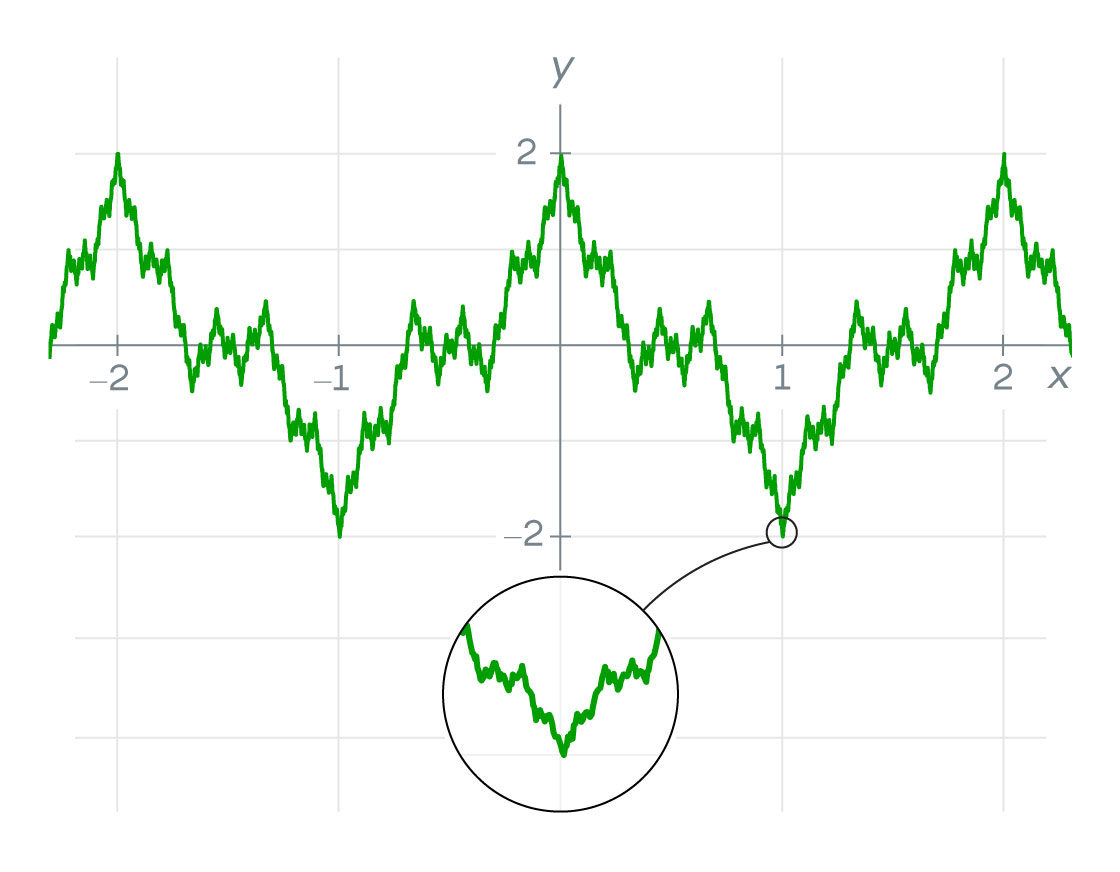
Many mathematicians dismissed the function. It was an anomaly, they said — the work of a pedant, mathematically useless. They couldn’t even visualize it. At first, when you try to plot the graph of Weierstrass’ function, it looks smooth in certain regions. Only by zooming in will you see that those regions are jagged, too, and that they’ll continue to get more serrated and badly behaved (what mathematicians call “pathological”) with each additional magnification.
But Weierstrass had proved beyond doubt that, though his function had no discontinuities, it was never differentiable. To show this, he first revisited the definitions of “continuity” and “differentiability” that had been formulated decades earlier by the mathematicians Augustin-Louis Cauchy and Bernard Bolzano. These definitions relied on vague, plain-language descriptions and inconsistent notation, making them easy to misinterpret.
So Weierstrass rewrote them, using precise language and concrete mathematical formulas. (Every calculus student learns the epsilon-delta definition of a limit; it was Weierstrass who introduced the modern version of it and used it as the foundation for his definitions of continuity and differentiability.)
He was then able to show that his function satisfied his more rigorous definition of continuity. At the same time, he could also prove that at every point, his new formal definition of the function’s derivative never had a finite value; it always “blew up” to infinity. In other words, continuity did not imply differentiability. His function was just as monstrous as mathematicians had feared.
The proof demonstrated that calculus could no longer rely on geometric intuition, as its inventors had done. It ushered in a new standard for the subject, one that was rooted in the careful analysis of equations. Mathematicians were forced to follow in Weierstrass’ footsteps, further sharpening their definition of functions, their understanding of the relationship between continuity and differentiability, and their methods for computing derivatives and integrals. This work to standardize calculus has since grown into the field known as analysis; Weierstrass is considered one of its founders.
But his function’s legacy extends far beyond the foundations of calculus and analysis. It revealed that mathematics is full of monsters: impossible-seeming functions, strange objects (it’s one of the earliest examples of a fractal), wild behaviors. “There’s a whole universe of possibilities, and the Weierstrass function is supposed to be opening your eyes to it,” said Philip Gressman of the University of Pennsylvania.
It also turned out to have many practical applications. In the early 20th century, physicists wanted to study Brownian motion, the random movement of particles in a liquid or gas. Because this movement is continuous but not smooth — characterized by rapid and infinitely tiny fluctuations — functions like Weierstrass’ were perfect for modeling it. Similarly, such functions have been used to model uncertainty in how people make decisions and take risks, as well as the complicated behavior of financial markets.
Much like Weierstrass himself, the consequences of his function have sometimes been late to bloom. But they’re continuing to shape mathematics and its applications today.



