Four Is Not Enough

Suppose you want to cover a standard 8-by-8 chessboard entirely with rectangular dominoes that each cover two squares on the board. It’s easy to imagine how you might do it: You could line the dominoes up horizontally, four in a row, or vertically, four in a column. You could arrange them like stairs, concentric squares or gnashing teeth. There are nearly 13 million ways to do it, and each arrangement requires exactly 32 dominoes, since the total area of the chessboard is 64 squares and each domino covers 2 squares.

But what happens if we remove a pair of opposite corners from the chessboard? How many ways can you cover this new board with 2-by-1 dominoes? Those unfamiliar with this classic problem may be surprised to learn that the answer is zero. It is impossible to cover this altered chessboard with 2-by-1 dominoes. How did we go from 13 million to zero so quickly? The answer is remarkably easy to find, if you know where to look.

The squares on a chessboard alternate in color, between dark and light. This has two important consequences for a standard 8-by-8 chessboard: First, there must be an equal number of dark and light squares, and second, opposing corners must be the same color. This means that when we remove a pair of opposite corners, the number of light squares that remain will be unequal to the number of dark squares. But every 2-by-1 domino must cover one dark square and one light square, which means a collection of dominos can only cover a chessboard with an equal number of dark and light squares. Our altered chessboard cannot be covered.

Of the many wonderful chessboard math problems, this one is my favorite because of its surprising solution. Who would expect the coloring of the squares to be the key to unlocking the puzzle? But mathematicians have been using colorings like this — which indicate structure and imply categorizations — to solve problems for a long time. And a recent advance in plane coloring has breathed new life into a problem that has stumped the mathematical community for over 60 years.

Consider the standard geometric plane, an infinite expanse of points in two dimensions. Your task is to color each of the infinitely many points in the plane. You might wish to color the entire plane red, or maybe half red and half blue, or maybe you’d splatter the color like in a Jackson Pollack painting. But there’s one rule in our plane coloring problem: If two points are exactly 1 unit apart, they cannot be the same color. Can you color every point in the plane without violating this rule?

“Of course!” you might say, “I’ll just use infinitely many colors.” There is a certain elegance to this sneaky approach (setting aside the philosophical question of whether infinitely many colors exist), but can you do it with finitely many colors? And if so, how many different colors would you need? Finding the minimum number of colors needed is known as the Hadwiger-Nelson problem, and it’s also often described as finding the “chromatic number” of the plane. (The chromatic number is a property of graphs, which are collections of vertices, or nodes, and the edges, or lines, that connect them. The chromatic number of a graph is the minimum number of colors needed to color all the vertices so that no two vertices connected by an edge are the same color. This is related to an alternate formulation of our plane coloring problem involving so-called unit-distance graphs.) The Hadwiger-Nelson problem was first posed nearly 70 years ago, and we still don’t know the minimum number of colors we would need. But the new result has narrowed down the possibilities. So, what are the possible numbers?

First, let’s see that finitely many colors will do. This red square will help us see why.

The red square above has side length $latex \frac {2}{3}$. Suppose you have two points in this square: How far apart could they be? The maximum distance between any two points in a square is equal to the length of the square’s diagonal, which we can compute using the Pythagorean theorem.

$latex d^2=\frac {2}{3}^2+\frac {2}{3}^2$

$latex d^2=\frac {4}{9}+\frac {4}{9}$

$latex d^2=\frac {8}{9}$

$latex d=\sqrt{\frac {8}{9}}$

And since

$latex \sqrt{\frac {8}{9}}<\sqrt{\frac {9}{9}}=\sqrt{1}=1$,

we know that the distance between any pair of points in this square is less than 1 unit. This means that we can color this whole square red and not violate our plane coloring rule.

Now, let’s make a bigger square out of nine of these little squares of side length $latex \frac {2}{3}$, and we’ll give each one its own color.

Since each square has a different color, we still have not violated our rule. Of course, since this large square (made of nine smaller squares) has a side length of 2, we’ve only covered 4 square units of the plane. But we can get the rest by copying and pasting!

We can cover the entire plane like this, but have we satisfied our rule about using different colors for points 1 unit apart? Just think about the red squares. We’ve already shown that no two points inside any one red square are 1 unit apart. Now, since each little square has side length 2/3, the minimum distance between any two distinct red squares is $latex \frac {2}{3}$ + $latex \frac {2}{3}$ = $latex \frac {4}{3}$, which means that any two points inside two different red squares will be more than 1 unit apart. Thus, no two red points in the plane are exactly 1 unit apart. And since the same argument applies to all nine colors, this is indeed a valid coloring of the plane in which no two points of the same color are exactly 1 unit apart. This shows not only that the chromatic number of the plane is finite, but it is at most 9.

A slightly more complicated argument using regular hexagons shows that seven colors are actually enough. You can surround a regular hexagon with six others and give them all different colors.

As with the squares above, you can extend this coloring in every direction.

By making the hexagon the right size — a diameter of slightly less than 1 will do — and extending the pattern correctly, we can be sure that no two points exactly 1 unit apart will be the same color.

So we’ve established an upper bound of 7 on the chromatic number of the plane. Can we easily establish a lower bound?

Well, it’s easy to see that we need more than one color. Take a point, P, in the plane: P needs a color, so let’s color it blue.

Since the plane extends infinitely in every direction, we know we can find a point, Q, that is exactly 1 unit away from P.

Point Q needs a color too, but our rule says Q can’t be blue. So we need a second color. Let’s color Q red.

Thus, the chromatic number of the plane is at least 2. Are two colors enough? Since the plane extends infinitely in every direction, there are actually infinitely many points 1 unit away from P. In fact, this is the definition of the circle of radius one centered at P.

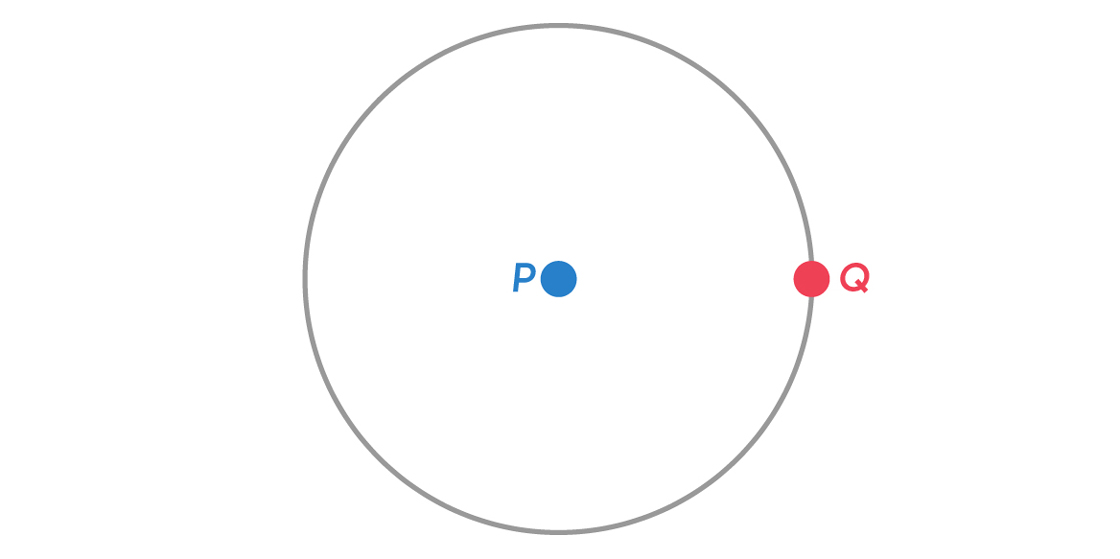
Since P is blue and every point on the circle is 1 unit away from P, no point on the circle can be blue. With only two colors, that would mean that every point on the circle would have to be red.

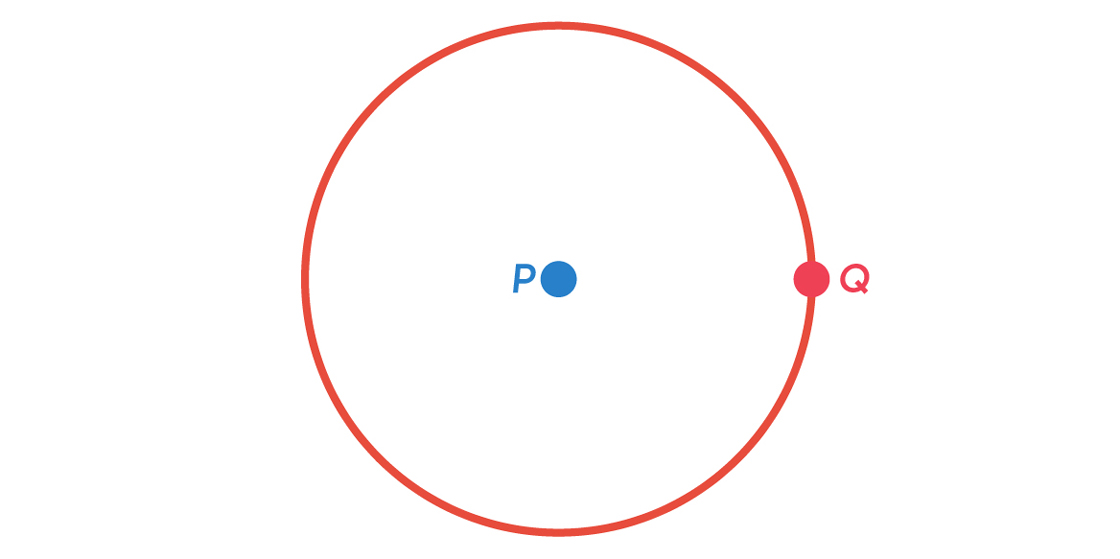
But now think about things from Q’s perspective: Nothing 1 unit from Q can be red. But, just as with P, there is an entire circle of points exactly 1 unit away from Q.

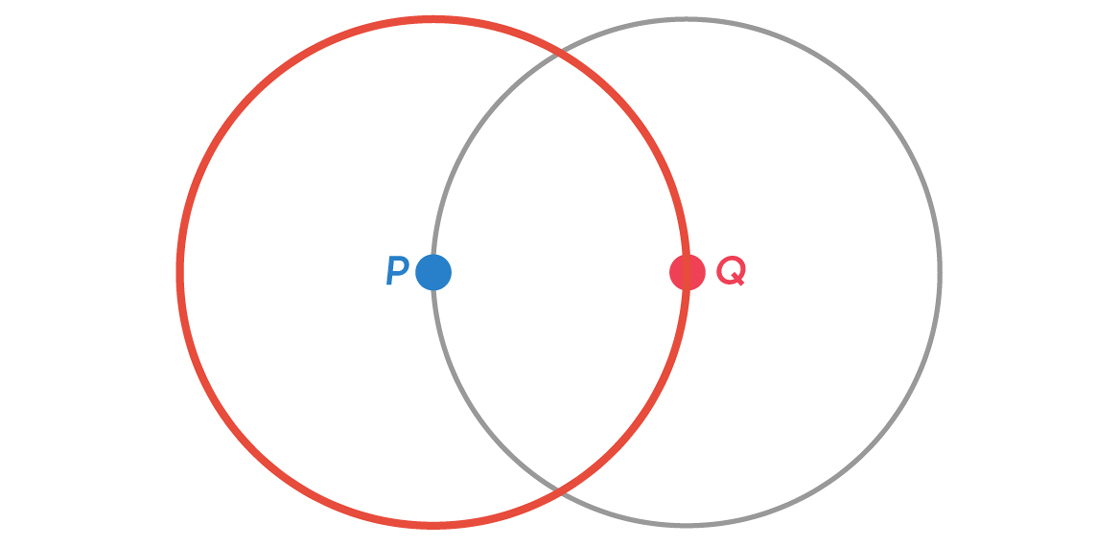
This new circle around Q intersects the red circle centered at P at two points: Let’s call them R and S. Points R and S can’t be blue, because they are 1 unit from P, and they can’t be red, because they are 1 unit from Q. So we need a third color. Let’s color R and S green.

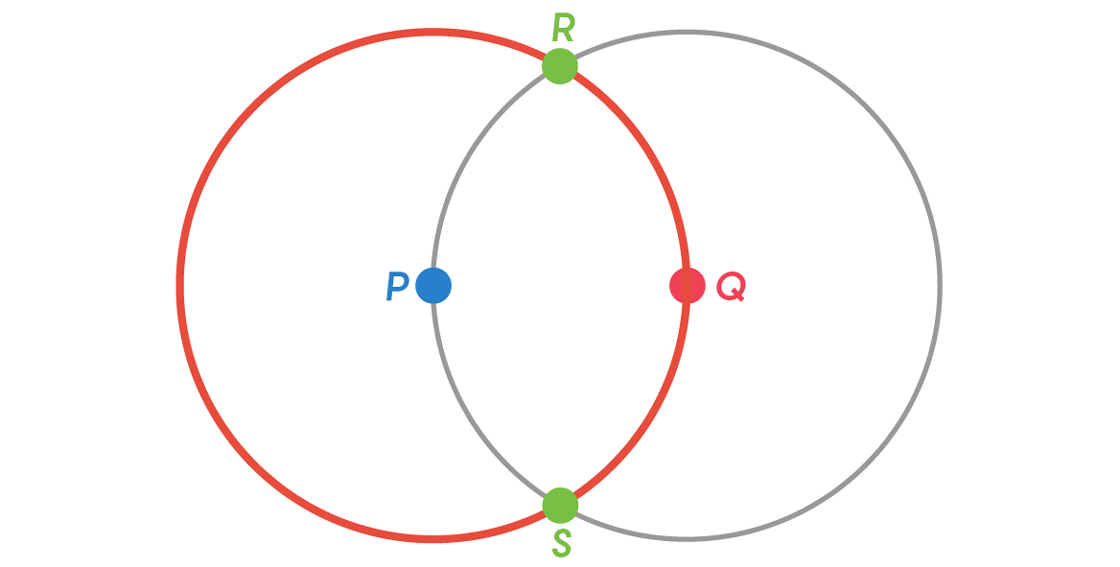
Notice the familiar geometric shapes emerging here: PQR and PQS are both equilateral triangles, and PSQR is a rhombus. Some elementary geometry shows us that $latex SR = \sqrt{3}>1$ , so we know it’s OK to color both S and R green.

This demonstrates that the chromatic number of the plane is at least 3. A clever trick will get us to 4. Consider that rhombus we just made.

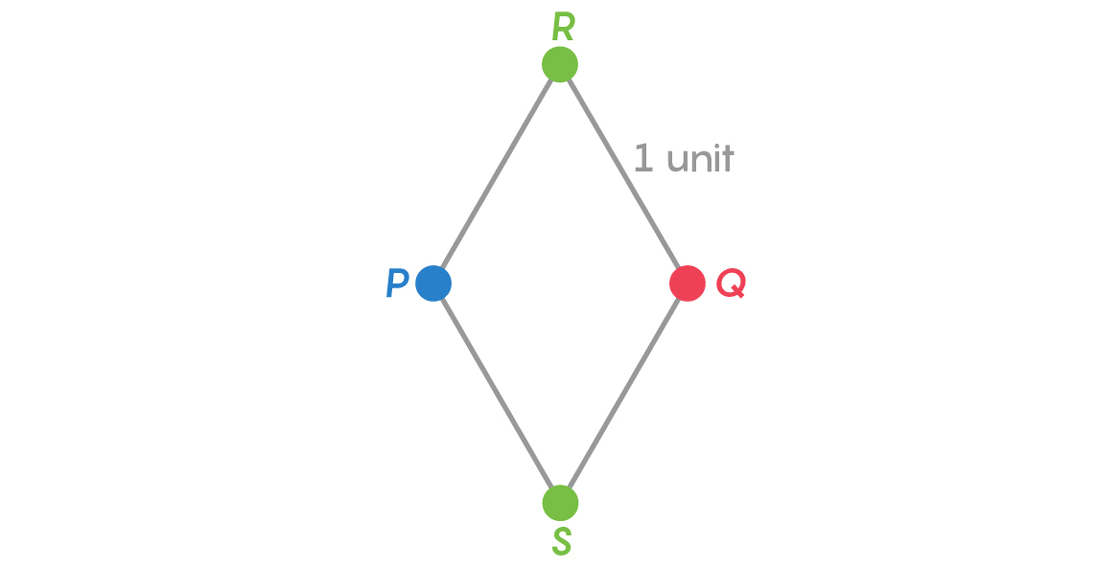
Suppose we have two copies of this rhombus sitting on top of each other. Imagine that we drive a nail through R, so that the two rhombuses hang like pictures on a wall. Now we grab the bottom vertices of the two rhombuses and slowly pull them apart.

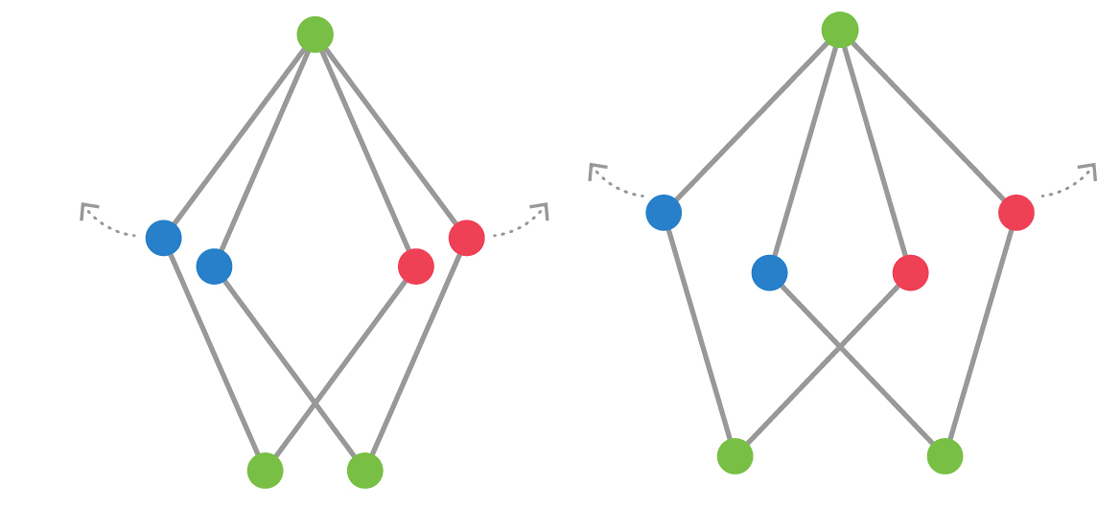
The rhombuses stay rigid as we pull them apart, and all the colorings remain valid. That is, until we pull them far enough apart so that the two bottom vertices are exactly 1 unit apart.

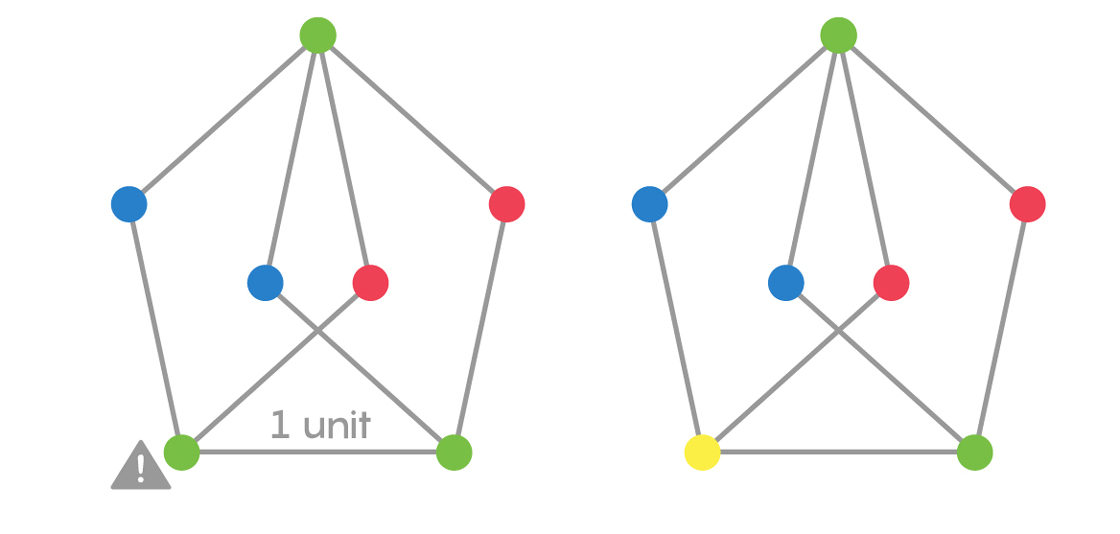
Now we have a problem. The two bottom vertices can’t both be green, because they are exactly 1 unit apart. Nor can they be red or blue. We need a fourth color! This diagram is called the Moser spindle, named after Leo and William Moser, and it proves that the chromatic number of the plane is at least 4.

In summary, we now know that the chromatic number of the plane is at least 4 but at most 7. And for nearly 60 years, this was everything we knew about the problem. Until Aubrey de Grey announced the discovery of this mathematical object in April 2018.

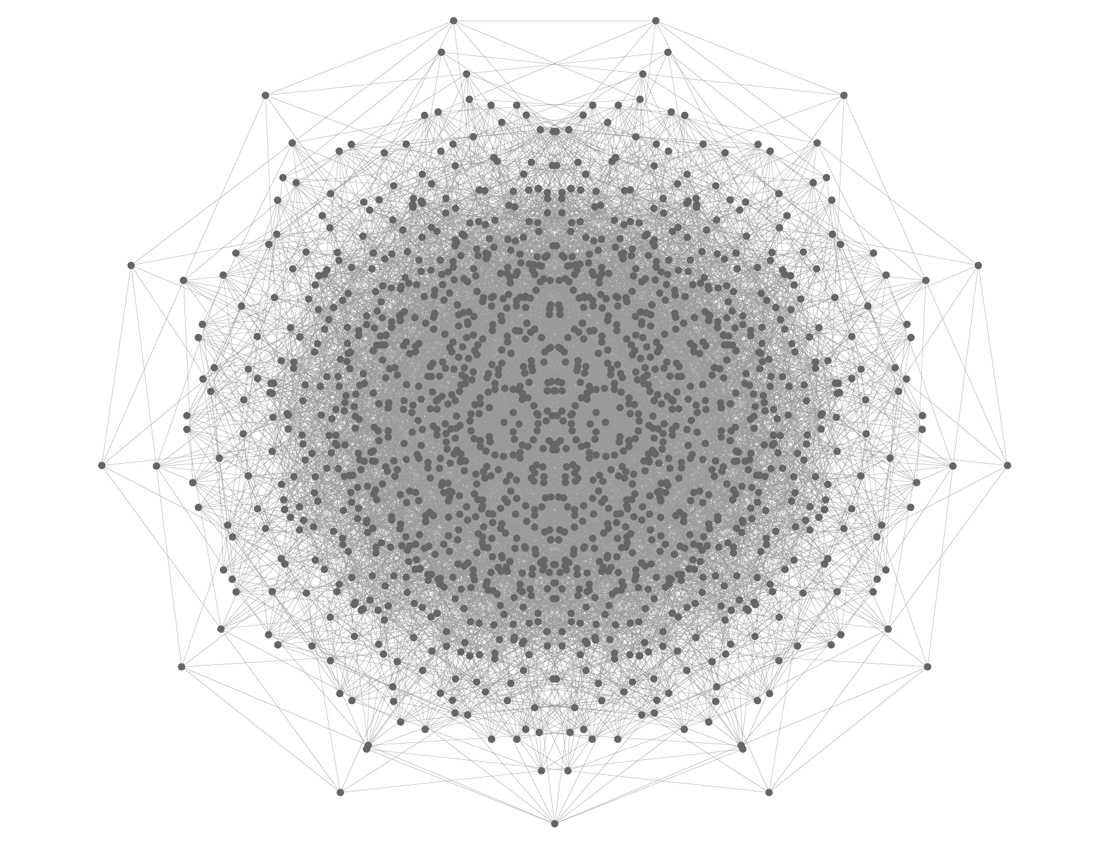
Just as the Moser spindle creates intricate interdependencies among its seven points that cannot be satisfied using only three colors, the 1,581-point construction by de Grey shown above cannot be colored using only four colors without a pair of points 1 unit apart being colored the same. But unlike with the Moser spindle, it’s not easy to see this just by looking — in fact, it takes a computer search to verify that four colors really aren’t enough. Thanks to de Grey’s discovery, we now know that the chromatic number of the plane is at least 5. Combined with our previous knowledge, that means we know that the chromatic number of the plane is either 5, 6 or 7. We just don’t know which!

This surprising result from de Grey, a biologist and recreational mathematician, has re-energized the mathematical community around the problem of coloring the plane. A collaborative online effort quickly sprang up to verify de Grey’s graph and find simpler versions (there are now examples using only around 800 points), and mathematicians are exploring whether de Grey’s techniques might be extended to get the lower bound to six colors or even seven. But some mathematicians suspect that the true answer to the Hadwiger-Nelson problem is unknowable, and that the chromatic number of the plane depends on independent issues like how we allow ourselves to think about and choose from infinite sets of points.

Still, there’s no question that de Grey’s result has gotten mathematicians excited about this elementary open problem, and many believe that an answer may be near at hand. Will we find it? Color me optimistic.

Download the “Four Is Not Enough” PDF worksheet to share with students.