The Prime Rib Problem

Dan Page for Quanta Magazine
Introduction
Let me tell you a fanciful story to prime you for this month’s puzzle. Hidden away in Manhattan’s East Village, a basement speak-easy serves a special delicacy of grilled prime ribs. No, it’s not the ribs you may be thinking of, but rather the ribs of a peculiar species of snake called Primivipera equicosta. Not only are the adults of this species inordinately long, but they have perfectly circular rib cages, and as their name implies, they have evenly spaced ribs that happen to be exactly 1 inch apart.
In order to bring out their exquisite flavor, the ribs have to be grilled evenly using a very fine wire that goes all the way around the middle of the rib. Without the wire, the rib cannot get properly cooked, but no metal should touch the snake at any point between two ribs. The chef achieves this by suspending the snake over coals in a long narrow trough using multiple rigid grilling frames, each of which is as long as the snake and consists of a long rod from which hang thin, evenly spaced wire rings that are a whole number of inches apart. In order to get perfect results, the chef insists, each grill must have evenly spaced rings any whole number of inches (except one) apart, with no missing rings. The chef is adamant that it must be so, though scientists are skeptical of these claims.
Several frames, each with differently spaced rings, are therefore carefully aligned, one on top of the other, and the snake is suspended so that it is encircled by the rings. All frames always start from the edge of the grilling pit, and the snake is always placed with its first rib 1 inch from the left edge. Thus, if a snake is suspended using three frames with wire rings spaced 2, 3 and 5 inches apart, out of the first 10 ribs, ribs 2, 3, 4, 5, 6, 8, 9 and 10 would be grilled properly but not ribs 1 or 7, as shown in the figure below.
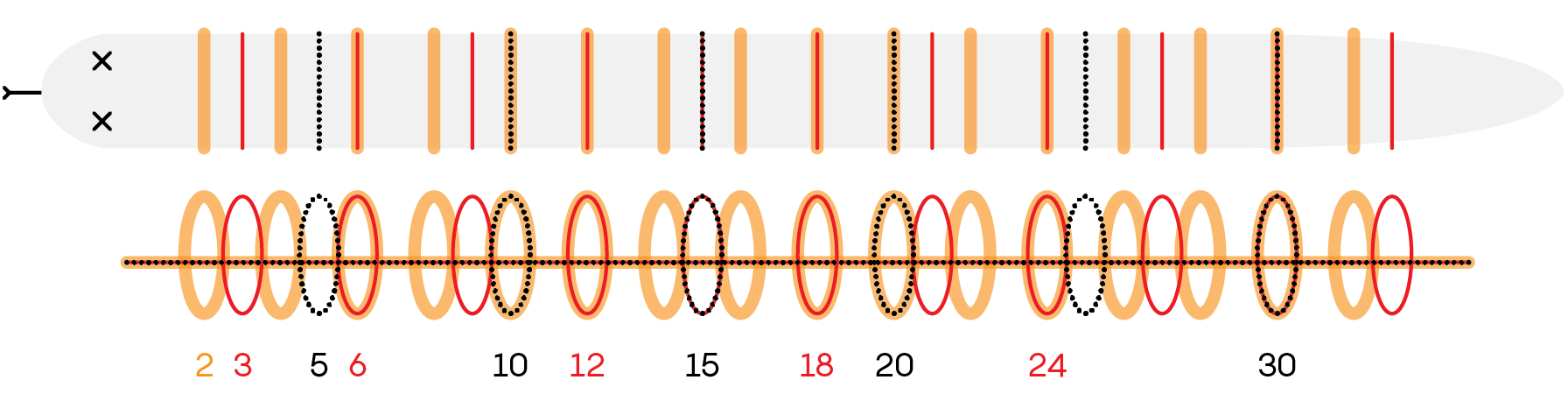
Once the snake is cooked, it is divided into portions by cutting out all the improperly cooked ribs. This creates uneven-sized edible portions, the smallest of which have just one cooked rib. In the above three-frame example, you’ll obtain a five-rib portion which includes ribs 2 through 6, a three-rib portion extending from rib 8 through rib 10, a one-rib portion for rib 12 and so on. The most prized and expensive dish is the largest portion — the one that has the maximum number of contiguous perfectly cooked ribs. Obviously, the size of this largest portion depends on the number of grilling frames used and the gaps between their rings. Using two frames with rings that are 2 inches apart in one and 3 inches apart in the other, the largest portions that a snake of any possible length can produce are three ribs long. The first such portion starts at rib 2: ribs 2 and 4 are cooked with the 2-inch-spaced frame and rib 3 with the 3-inch-spaced one.
That completes the story of this how this unique dish is prepared and the intricate conditions that are thought to be required to achieve perfect results. I now have two sets of questions for you that are inverses of each other.
Problem 1
If you are free to use five grills with any spacing (except a 1 inch gap, of course), what is the largest sized well-cooked portion you could create, one that includes the maximum number of ribs possible? And what’s the shortest length of snake that can yield this maximum portion? Obviously, this question can be generalized to any number of grills. Ambitious readers can amuse themselves by calculating the answers for higher numbers of grills such as nine. Note that you can use brute force searches, but the length of snake required for larger numbers of grills soon becomes astronomical, requiring snakes as long as the constellation Serpens is wide. Such computations are known as models of high computation complexity. So some cleverness will surely be required.
Problem 2
What’s the smallest number of grills that can yield maximum portions of 50, 100 and (gasp!) 150 ribs? What are the smallest sized cosmic serpents that will be required for these? Note that the latter question for 100 and 150 are open problems, at least for me. Perhaps one of you will provide answers that can be proved to be the smallest. This may require heavy-duty mathematical tools but even they may not be able to give a provably correct answer. However, there is scope for cleverness and tinkering, and we may be able to find heuristic methods that generate some plausible candidates.
No doubt by now you will have seen the connection to prime numbers implicit in the details (and title) of this puzzle. Prime numbers are connected to an endless source of unsolved problems in number theory, such as the famous Riemann hypothesis, whose solution carries a prize of $1 million from the Clay Mathematics Institute, and which some physicists are attacking using quantum mechanics. Primes invoke in mathematicians a deep sense of awe and continue to inspire new generations of researchers, such as Kaisa Matomäki, who “dreams of primes.”
The above story is an attempt to come up with a physical situation that naturally mimics the Sieve of Eratosthenes. I’ve enjoyed this challenge, but let me now throw this out to readers. Can you come up with even remotely plausible situations in which the prime number sieve might occur naturally?
Happy puzzling, and I look forward to seeing your comments.
Editor’s note: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt. And if you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION.” (It will not appear online, so solutions to the puzzle above should be submitted separately.)
Note that we may hold comments for the first day or two to allow for independent contributions by readers.
Update: The solution has been published here.



