Tinkertoy Models Produce New Geometric Insights

For more than 100 years, mathematicians have investigated a fact about geometric objects that is so basic that — like breathing air — you need to think a moment to realize it’s even there: What a geometric object looks like depends a lot on the space in which you visualize it.

For instance, draw a circle on a piece of paper. It’s such a routine maneuver that it’s easy to miss what you’re really doing: You’re taking a circle and “embedding” it in two-dimensional space. But don’t stop there. Let the circle float in the air in front of you to embed it in three-dimensional space. The addition of a third dimension gives you more flexibility. Like a loop of string, you can tilt the circle any number of ways. You can even tie it in a knot.

“That’s the zeroth thing to internalize — an object inherits something from the larger space inside which it sits,” said Dhruv Ranganathan, a mathematician at the Massachusetts Institute of Technology.

In math, shapes are often represented by equations. But those equations are not intrinsic properties of the shapes. The equations that describe the circle differ depending on whether you’re visualizing it in two-dimensional or three-dimensional space. Sometimes there are no equations that describe a shape in a space. For example, there are no equations that describe what a circle looks like in one-dimensional space, which is just another way of saying that the circle doesn’t “fit” into one-dimensional space.

For more than a century, mathematicians have investigated the equations required to describe — or embed — different kinds of shapes in spaces with different numbers of dimensions. They ask questions like, “Do equations exist that describe this shape in that space?” and “How complicated are the equations required to describe a given shape in space?” Now, in a pair of recent papers, mathematicians have moved closer to developing a systematic understanding of how those equations vary based on the shape they describe.

The results are striking. So are the techniques behind them. They come from a field of mathematics known as tropical geometry, where mathematicians build Tinkertoy models of complicated geometric objects in order to gain a vantage on the objects’ geometry. In exploring the relationship between a shape and its embedding, tropical geometers have shown that their sticklike models remember far more about their original shapes than you could possibly imagine.

The Right Box for a Shape

A circle has just one intrinsic property — its radius. If you know the radius, you know the circle.

Now sketch a circle on the page. By situating, or embedding, the circle in two-dimensional space you’ve given it another trait — an algebraic equation that describes what the circle looks like. That equation, x²+ y²= 1, carves out the points on the circle from all other points in the space.

But move to three-dimensional space and suddenly that equation doesn’t describe the circle. Instead you need two equations, x²+ y²= 1 and also, in the simplest case, z= 0. The circle is where those two graphs intersect.

You might ask: What are the simplest equations that will embed a shape into space? By “simplest,” mathematicians want to know two things: How many variables does it need? And what’s the highest power of those variables? For example, the simplest equation that describes the circle requires two variables raised to the second power. Mathematicians say that its “rank” (the number of variables needed) is 2, and its “degree” (the largest exponent needed) is also 2. Understanding the nature of the equations required to embed a shape in space also provides mathematicians with a deeper understanding of the shape itself — similar to how you could learn something about the shape of a physical object by trying to fit it inside various boxes.

“Often to really understand [a shape] or classify it, to get a finer feel for its geometry, we’re going to embed it somewhere,” said Sam Payne, a mathematician at the University of Texas, Austin, and co-author of some of the recent work.

Nearly 40 years ago, the mathematicians Phillip Griffiths and Joseph Harris proved a relationship between the number of holes that the shape has (a donut, for instance, has one hole) and the simplest equations required to describe that shape in space. By proving the “Brill-Noether” theorem, they were able to predict whether a generic shape with a given number of holes can be embedded by equations of given rank and degree.

In 2006, a mathematician at the Georgia Institute of Technology named Matt Baker realized it was possible to build a new proof of the theorem using techniques drawn entirely from the upstart field of tropical geometry. He demonstrated a way of degenerating complicated shapes into simple configurations of lines, similar to reducing a skyscraper to its skeleton frame. Somehow the simplified model retains enough information about the original object to recover information about the equations that embed that object.

“You prove the number you wanted to compute is the same in the tropical world and the classical world, but often the tropical thing will be easier to compute,” said Baker.

Stick Figures

To get a feel for how tropical geometry works, imagine a circle made of string. Place your fingers on four points along its circumference and pull those points outward. Eventually the circle becomes a square.

Many properties of the circle don’t survive the transformation — the circle’s smooth curvature is gone, and the area inside the square is less than the area inside the circle. But some properties do. For instance, the square and the circle have the same perimeter. And, crucially, the square’s perimeter is easier to calculate than the circle’s. You’ve gained a computational advantage.

“Maybe it’s complicated to measure length while in a circle because there’s pi involved, but it’s easy when a square because you can use a ruler,” said Ranganathan.

Tropical geometers don’t typically use string. Instead they use a process called “degenerating” or “tropicalizing” a geometric object. They might start with a sumptuous higher-dimensional shape, apply certain algebraic manipulations, and end up with something that looks like a handful of twigs scattered on the ground. For example, through the tropicalization process, this shape:

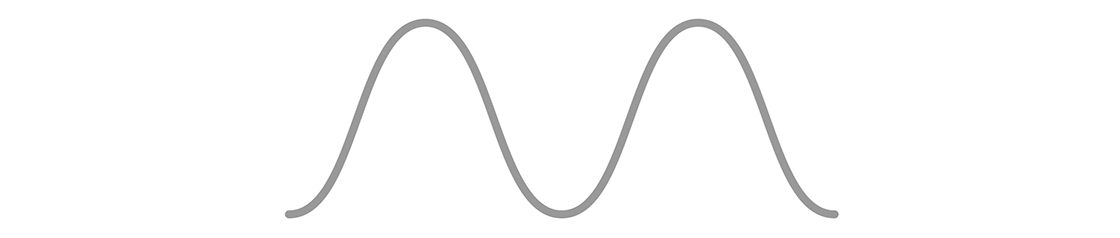
Turns into this collection of lines:

The lines themselves are boring — they’re too simple on their own to tell you anything interesting about the object they descend from. “What is interesting is the combinatorics of how those lines meet,” said David Jensen, a tropical geometer at the University of Kentucky and co-author of the new results.

To study the combinatorics, tropical geometers perform another transformation: They turn the lines into a graph. The graph is like a mirror image of the collection of lines. Each vertex in the graph represents one of the lines, and each edge in the graph represents an intersection between two lines (so two vertices will be connected by an edge if the two lines represented by those vertices intersect). In that way, the above collection of lines turns into this graph:

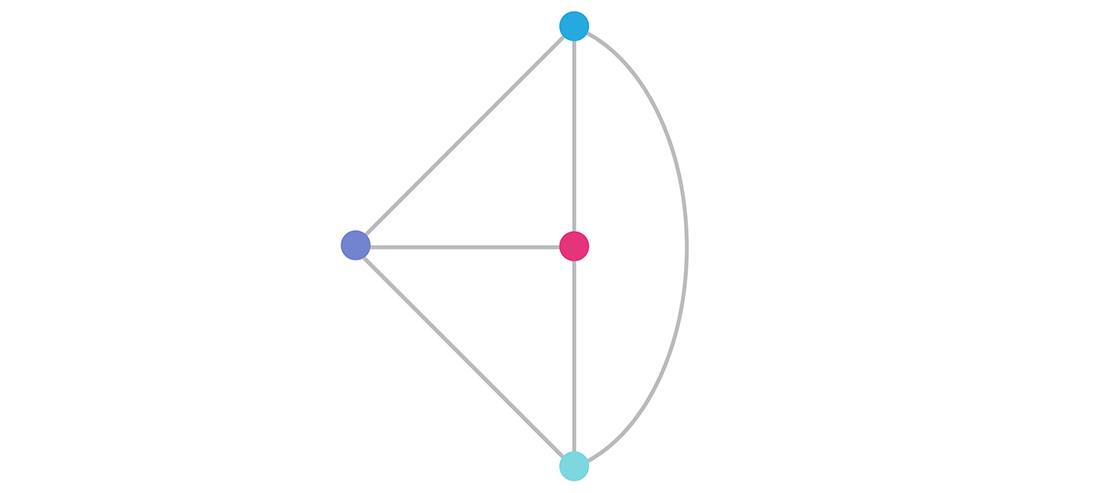
The graph is easy to work with but still retains information about the geometric object it came from — much more information, in fact, than mathematicians recognized at first. “We’re realizing more and more information seems to survive this brutal, forgetful process,” said Ranganathan.

That includes information about the equations that embed the main geometric object. Recent work by Jensen, Payne and Ranganathan has shown how the properties of those equations can be extracted through a game called chip firing.

To play this game, distribute some number of poker chips on the vertices of a graph. You’re working against an opponent who can take chips away. Your objective is to move chips around so that no vertex ever ends up with a negative number of chips.

Here’s the catch: You can only move chips in a specific manner called chip firing. To do it, point to a vertex. That vertex fires a chip to each of its neighboring vertices. (If you fire a vertex that has more neighbors than chips, the vertex assumes a negative value.)

After you distribute your chips, your opponent removes some number of chips from one vertex (the precise number becomes important later). You then reallocate your chips through a series of chip-firing moves. If, at the end of those moves, no vertex has a negative value, you win.

Chip firing has deep mathematical consequences. In tropical geometry, every shape can be transformed into a graph. And that graph creates a unique game board. By studying the cases where you can win — the number of chips you need to start with, and the number of chips that your opponent can remove — mathematicians reveal the nature of the equations needed to embed the shape related to that graph.

For example, if you start with three chips, your opponent removes two, and you win the game, then you know that very likely the underlying shape can be embedded with an equation of rank two (two variables) and degree three (raised to the third power).

“For some miraculous reason,” said Ranganathan, “the extent to which you can play this game on a graph and win or not win is related to whether or not you can write down equations for an algebraic curve in a certain way.”

The Hole Story

The Brill-Noether theorem establishes an approximate relationship between a geometric object and its embedding. It takes into account only the number of holes in the object (its “genus”), and it says only that a certain embedding exists with high probability (rather than with certainty).

But geometric objects can have other intrinsic properties. Recent work in tropical geometry looks at properties besides the genus in order to make even more exact predictions about embedding equations.

In January 2017, Ranganathan and Jensen used tropical techniques to relate the degree and rank of embedding equations to the property of a geometric object known as its “gonality” (which is a measure of the kinds of functions that can be associated to a shape). And in August of this year, Jensen and Payne employed tropical geometry to prove cases of a related problem known as the “strong maximal rank” conjecture.^*

Together these proofs refine mathematicians’ understanding of how geometric objects can be represented algebraically. They also add credence to the strange geometric transformations achieved in tropical geometry.