To Test Einstein’s Equations, Poke a Black Hole

In November 1915, in a lecture before the Prussian Academy of Sciences, Albert Einstein described an idea that upended humanity’s view of the universe. Rather than accepting the geometry of space and time as fixed, Einstein explained that we actually inhabit a four-dimensional reality called space-time whose form fluctuates in response to matter and energy.

Einstein elaborated this dramatic insight in several equations, referred to as his “field equations,” that form the core of his theory of general relativity. That theory has been vindicated by every experimental test thrown at it in the century since.

Yet even as Einstein’s theory seems to describe the world we observe, the mathematics underpinning it remain largely mysterious. Mathematicians have been able to prove very little about the equations themselves. We know they work, but we can’t say exactly why. Even Einstein had to fall back on approximations, rather than exact solutions, to see the universe through the lens he’d created.

Over the last year, however, mathematicians have brought the mathematics of general relativity into sharper focus. Two groups have come up with proofs related to an important problem in general relativity called the black hole stability conjecture. Their work proves that Einstein’s equations match a physical intuition for how space-time should behave: If you jolt it, it shakes like Jell-O, then settles down into a stable form like the one it began with.

“If these solutions were unstable, that would imply they’re not physical. They’d be a mathematical ghost that exists mathematically and has no significance from a physical point of view,” said Sergiu Klainerman, a mathematician at Princeton University and co-author, with Jérémie Szeftel, of one of the two new results.

To complete the proofs, the mathematicians had to resolve a central difficulty with Einstein’s equations. To describe how the shape of space-time evolves, you need a coordinate system — like lines of latitude and longitude — that tells you which points are where. And in space-time, as on Earth, it’s hard to find a coordinate system that works everywhere.

Shake a Black Hole

General relativity famously describes space-time as something like a rubber sheet. Absent any matter, the sheet is flat. But start dropping balls onto it — stars and planets — and the sheet deforms. The balls roll toward one another. And as the objects move around, the shape of the rubber sheet changes in response.

Einstein’s field equations describe the evolution of the shape of space-time. You give the equations information about curvature and energy at each point, and the equations tell you the shape of space-time in the future. In this way, Einstein’s equations are like equations that model any physical phenomenon: This is where the ball is at time zero, this is where it is five seconds later.

“They’re a mathematically precise quantitative version of the statement that space-time curves in the presence of matter,” said Peter Hintz, a Clay research fellow at the University of California, Berkeley, and co-author, with András Vasy, of the other recent result.

In 1916, almost immediately after Einstein released his theory of general relativity, the German physicist Karl Schwarzschild found an exact solution to the equations that describes what we now know as a black hole (the term wouldn’t be invented for another five decades). Later, physicists found exact solutions that describe a rotating black hole and one with an electrical charge.

These remain the only exact solutions that describe a black hole. If you add even a second black hole, the interplay of forces becomes too complicated for present-day mathematical techniques to handle in all but the most special situations.

Yet you can still ask important questions about this limited group of solutions. One such question developed out of work in 1952 by the French mathematician Yvonne Choquet-Bruhat. It asks, in effect: What happens when you shake a black hole?  

This problem is now known as the black hole stability conjecture. The conjecture predicts that solutions to Einstein’s equations will be “stable under perturbation.” Informally, this means that if you wiggle a black hole, space-time will shake at first, before eventually settling down into a form that looks a lot like the form you started with. “Roughly, stability means if I take special solutions and perturb them a little bit, change data a little bit, then the resulting dynamics will be very close to the original solution,” Klainerman said.

So-called “stability” results are an important test of any physical theory. To understand why, it’s useful to consider an example that’s more familiar than a black hole.

Imagine a pond. Now imagine that you perturb the pond by tossing in a stone. The pond will slosh around for a bit and then become still again. Mathematically, the solutions to whatever equations you use to describe the pond (in this case, the Navier-Stokes equations) should describe that basic physical picture. If the initial and long-term solutions don’t match, you might question the validity of your equations.

“This equation might have whatever properties, it might be perfectly fine mathematically, but if it goes against what you expect physically, it can’t be the right equation,” Vasy said.

For mathematicians working on Einstein’s equations, stability proofs have been even harder to find than solutions to the equations themselves. Consider the case of flat, empty Minkowski space — the simplest of all space-time configurations. This solution to Einstein’s equations was found in 1908 in the context of Einstein’s earlier theory of special relativity. Yet it wasn’t until 1993 that mathematicians managed to prove that if you wiggle flat, empty space-time, you eventually get back flat, empty space-time. That result, by Klainerman and Demetrios Christodoulou, is a celebrated work in the field.

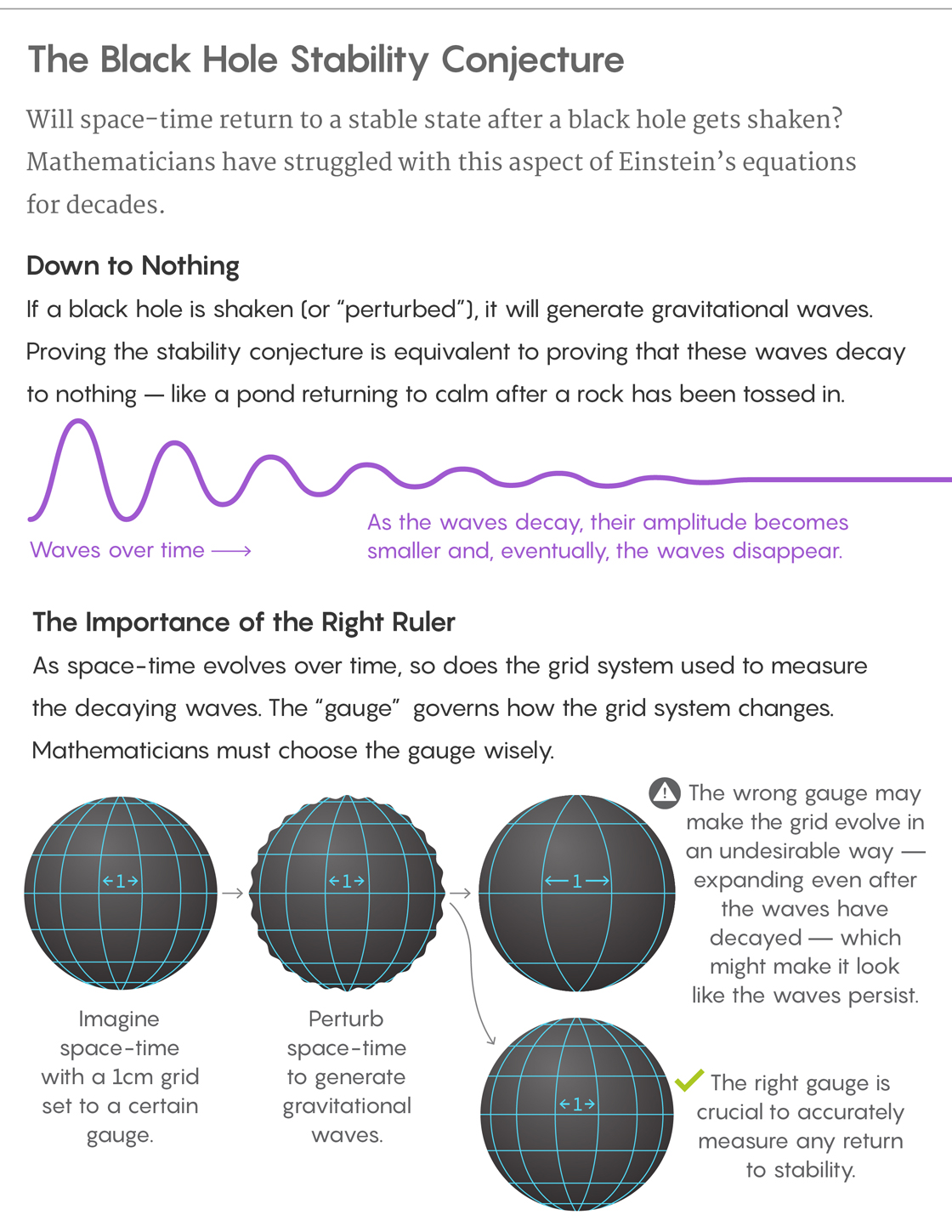
One of the main difficulties with stability proofs has to do with keeping track of what is going on in four-dimensional space-time as the solution evolves. You need a coordinate system that allows you to measure distances and identify points in space-time, just as lines of latitude and longitude allow us to define locations on Earth. But it’s not easy to find a coordinate system that works at every point in space-time and then continues to work as the shape of space-time evolves.

“We don’t know of a one-size-fits-all way to do this,” Hintz wrote in an email. “After all, the universe does not hand you a preferred coordinate system.”

The Measurement Problem

The first thing to recognize about coordinate systems is that they’re a human invention. The second is that not every coordinate system works to identify every point in a space.

Take lines of latitude and longitude: They’re arbitrary. Cartographers could have anointed any number of imaginary lines to be 0 degrees longitude. And while latitude and longitude work to identify just about every location on Earth, they stop making sense at the North and South poles. If you knew nothing about Earth itself, and only had access to latitude and longitude readings, you might wrongly conclude there’s something topologically strange going on at those points.

This possibility — of drawing wrong conclusions about the properties of physical space because the coordinate system used to describe it is inadequate — is at the heart of why it’s hard to prove the stability of space-time.

“It could be the case that stability is true, but you’re using coordinates that are not stable and thus you miss the fact that stability is true,” said Mihalis Dafermos, a mathematician at the University of Cambridge and a leading figure in the study of Einstein’s equations.

In the context of the black hole stability conjecture, whatever coordinate system you’re using has to evolve as the shape of space-time evolves — like a snugly fitting glove adjusting as the hand it encloses changes shape. The fit between the coordinate system and space-time has to be good at the start and remain good throughout. If it doesn’t, there are two things that can happen that would defeat efforts to prove stability.

First, your coordinate system might change shape in a way that makes it break down at certain points, just as latitude and longitude fail at the poles. Such points are called “coordinate singularities” (to distinguish them from physical singularities, like an actual black hole). They are undefined points in your coordinate system that make it impossible to follow an evolving solution all the way through.

Second, a poorly fitting coordinate system might disguise the underlying physical phenomena it’s meant to measure. To prove that solutions to Einstein’s equations settle down into a stable state after being perturbed, mathematicians must keep careful track of the ripples in space-time that are set in motion by the perturbation. To see why, it’s worth considering the pond again. A rock thrown into a pond generates waves. The long-term stability of the pond results from the fact that those waves decay over time — they grow smaller and smaller until there’s no sign they were ever there.

The situation is similar for space-time. A perturbation will set off a cascade of gravitational waves, and proving stability requires proving that those gravitational waves decay. And proving decay requires a coordinate system — referred to as a “gauge” — that allows you to measure the size of the waves. The right gauge allows mathematicians to see the waves flatten and eventually disappear altogether.

“The decay has to be measured relative to something, and it’s here where the gauge issue shows up,” Klainerman said. “If I’m not in the right gauge, even though in principle I have stability, I can’t prove it because the gauge will just not allow me to see that decay. If I don’t have decay rates of waves, I can’t prove stability.”

The trouble is, while the coordinate system is crucial, it’s not obvious which one to choose. “You have a lot of freedom about what this gauge condition can be,” Hintz said. “Most of these choices are going to be bad.”

Partway There

A full proof of the black hole stability conjecture requires proving that all known black hole solutions to Einstein’s equations (with the spin of the black hole below a certain threshold) are stable after being perturbed. These known solutions include the Schwarzschild solution, which describes space-time with a nonrotating black hole, and the Kerr family of solutions, which describe configurations of space-time empty of everything save a single rotating black hole (where the properties of that rotating black hole — its mass and angular momentum — vary within the family of solutions).

Both of the new results make partial progress toward a proof of the full conjecture.

Hintz and Vasy, in a paper posted to the scientific preprint site arxiv.org in 2016, proved that slowly rotating black holes are stable. But their work did not cover black holes rotating above a certain threshold.

Their proof also makes some assumptions about the nature of space-time. The original conjecture is in Minkowski space, which is not just flat and empty but also fixed in size. Hintz and Vasy’s proof takes place in what’s called de Sitter space, where space-time is accelerating outward, just like in the actual universe. This change of setting makes the problem simpler from a technical point of view, which is easy enough to appreciate at a conceptual level: If you drop a rock into an expanding pond, the expansion is going to stretch the waves and cause them to decay faster than they would have if the pond were not expanding.   

“You’re looking at a universe undergoing an accelerated expansion,” Hintz said. “This makes the problem a little easier as it appears to dilute the gravitational waves.”

Klainerman and Szeftel’s work has a slightly different flavor. Their proof, the first part of which was posted online last November, takes place in Schwarzschild space-time — closer to the original, more difficult setting for the problem. They prove the stability of a nonrotating black hole, but they do not address solutions in which the black hole is spinning. Moreover, they only prove the stability of black hole solutions for a narrow class of perturbations — where the gravitational waves generated by those perturbations are symmetric in a certain way.

Both results involve new techniques for finding the right coordinate system for the problem. Hintz and Vasy start with an approximate solution to the equations, based on an approximate coordinate system, and gradually increase the precision of their answer until they arrive at exact solutions and well-behaved coordinates. Klainerman and Szeftel take a more geometric approach to the challenge.

The two teams are now trying to build on their respective methods to find a proof of the full conjecture. Some expert observers think the day might not be far off.

“I really think things are now at the stage that the remaining difficulties are just technical,” Dafermos said. “Somehow one doesn’t need new ideas to solve this problem.” He emphasized that a final proof could come from any one of the large number of mathematicians currently working on the problem.

For 100 years Einstein’s equations have served as a reliable experimental guide to the universe. Now mathematicians may be getting closer to demonstrating exactly why they work so well.

This article was reprinted on ScientificAmerican.com.