What Is Entropy? A Measure of Just How Little We Really Know.

Kristina Armitage/Quanta Magazine
Introduction
Life is an anthology of destruction. Everything you build eventually breaks. Everyone you love will die. Any sense of order or stability inevitably crumbles. The entire universe follows a dismal trek toward a dull state of ultimate turmoil.
To keep track of this cosmic decay, physicists employ a concept called entropy. Entropy is a measure of disorderliness, and the declaration that entropy is always on the rise — known as the second law of thermodynamics — is among nature’s most inescapable commandments.
I have long felt haunted by the universal tendency toward messiness. Order is fragile. It takes months of careful planning and artistry to craft a vase but an instant to demolish it with a soccer ball. We spend our lives struggling to make sense of a chaotic and unpredictable world, where any attempt to establish control seems only to backfire. The second law demands that machines can never be perfectly efficient, which implies that whenever structure arises in the universe, it ultimately serves only to dissipate energy further — be it a star that eventually explodes or a living organism converting food into heat. We are, despite our best intentions, agents of entropy.
“Nothing in life is certain except death, taxes and the second law of thermodynamics,” wrote Seth Lloyd, a physicist at the Massachusetts Institute of Technology. There’s no sidestepping this directive. The growth of entropy is deeply entwined with our most basic experiences, accounting for why time runs forward and why the world appears deterministic rather than quantum mechanically uncertain.
But despite its fundamental importance, entropy is perhaps the most divisive concept in physics. “Entropy has always been a problem,” Lloyd told me. The confusion stems in part from the way the term gets tossed and twisted between disciplines — it has similar but distinct meanings in everything from physics to information theory to ecology. But it’s also because truly wrapping one’s head around entropy requires taking some deeply uncomfortable philosophical leaps.
As physicists have worked to unite seemingly disparate fields over the past century, they have cast entropy in a new light — turning the microscope back on the seer and shifting the notion of disorder to one of ignorance. Entropy is seen not as a property intrinsic to a system but as one that’s relative to an observer who interacts with that system. This modern view illuminates the deep link between information and energy, which is now helping to usher in a mini-industrial revolution on the smallest of scales.
Two hundred years after the seeds of entropy were first sown, what’s emerging is a conception of this quantity that’s more opportunistic than nihilistic. The conceptual evolution is upending the old way of thinking, not just about entropy, but about the purpose of science and our role in the universe.
The Motive Power of Fire
The notion of entropy grew out of an attempt at perfecting machinery during the industrial revolution. A 28-year-old French military engineer named Sadi Carnot set out to calculate the ultimate efficiency of the steam-powered engine. In 1824, he published a 118-page book titled Reflections on the Motive Power of Fire, which he sold on the banks of the Seine for 3 francs. Carnot’s book was largely disregarded by the scientific community, and he died several years later of cholera. His body was burned, as were many of his papers. But some copies of his book survived, and in them lay the embers of a new science of thermodynamics — the motive power of fire.
Carnot realized that the steam engine is, at its core, a machine that exploits the tendency for heat to flow from hot objects to cold ones. He drew up the most efficient engine conceivable, instituting a bound on the fraction of heat that can be converted to work, a result now known as Carnot’s theorem. His most consequential statement comes as a caveat on the last page of the book: “We should not expect ever to utilize in practice all the motive power of combustibles.” Some energy will always be dissipated through friction, vibration, or another unwanted form of motion. Perfection is unattainable.
Reading through Carnot’s book a few decades later, in 1865, the German physicist Rudolf Clausius coined a term for the proportion of energy that’s locked up in futility. He called it “entropy,” after the Greek word for transformation. He then laid out what became known as the second law of thermodynamics: “The entropy of the universe tends to a maximum.”
Physicists of the era erroneously believed that heat was a fluid (called “caloric”). Over the following decades, they realized heat was rather a byproduct of individual molecules bumping around. This shift in perspective allowed the Austrian physicist Ludwig Boltzmann to reframe and sharpen the idea of entropy using probabilities.
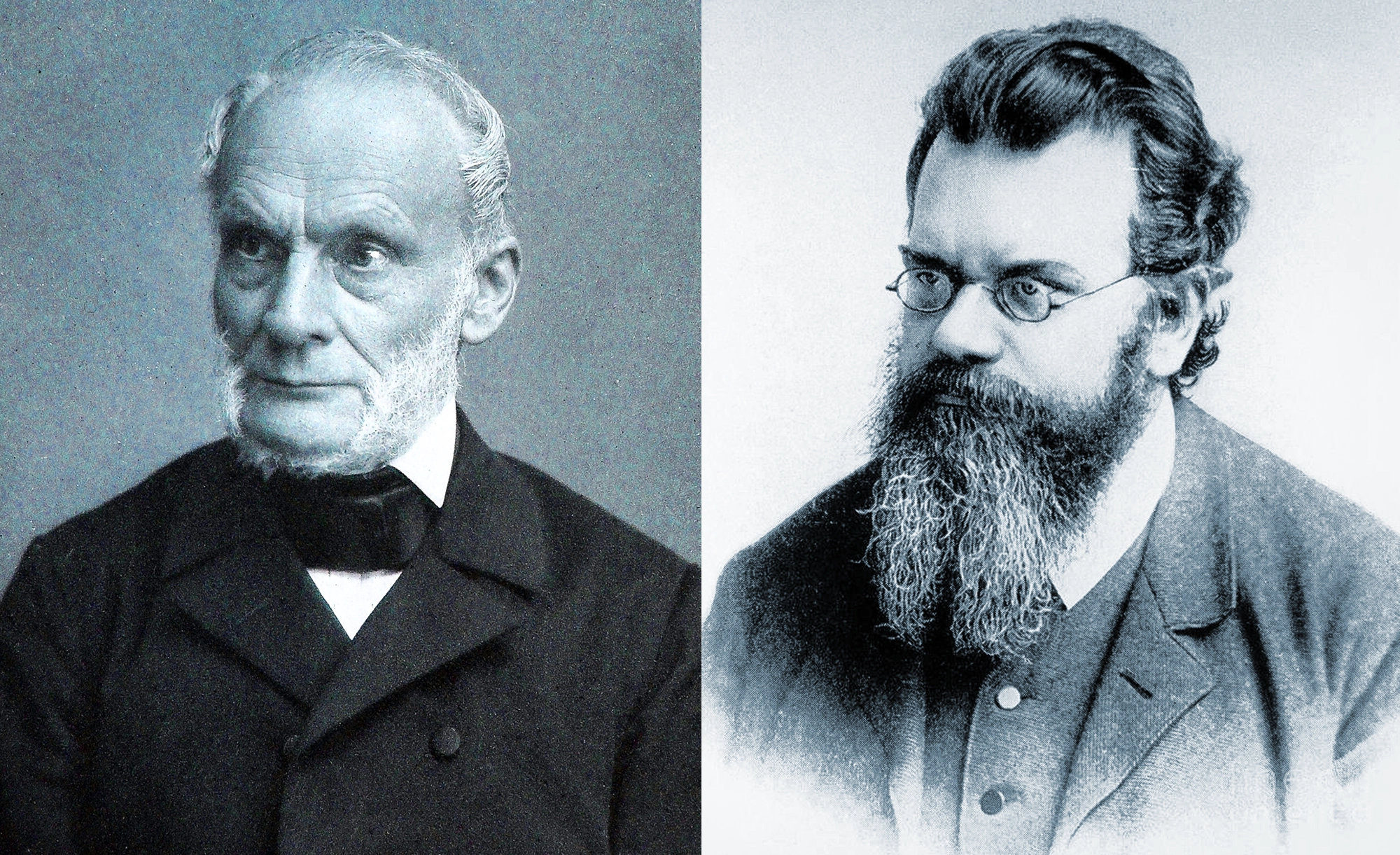
Rudolf Clausius (left) originated the insight that entropy tends to increase. Ludwig Boltzmann rooted this rise in statistical mechanics.
Theo Schafgans (left); Creative Commons
Boltzmann distinguished the microscopic properties of molecules, such as their individual locations and velocities, from bulk macroscopic properties of a gas like temperature and pressure. Consider, instead of a gas, a group of identical game pieces on a checkerboard. The list of exact coordinates of all the checkers is what Boltzmann called a “microstate,” and their overall configuration — whether they form a star, say, or are all lumped together — is a “macrostate.” Boltzmann defined the entropy of a given macrostate in terms of the number of possible microstates that give rise to it. A high-entropy macrostate is one that has many compatible microstates — many possible arrangements of checkers that yield that same overall pattern.
There are only so many ways the checkers can take on specific shapes that appear ordered, while there are drastically more ways for them to look randomly scattered across the board. Thus, entropy can be seen as a measure of disorder. The second law becomes an intuitive probabilistic statement: There are more ways for something to look messy than clean, so, as the parts of a system randomly shuffle through different possible configurations, they tend to take on arrangements that appear messier and messier.
The heat in Carnot’s engine flows from hot to cold because it’s more probable for the gas particles to be all mixed up rather than segregated by speed — with hot, fast-moving particles on one side and cold, slow-moving ones on the other. The same reasoning applies to why glass shatters, ice melts, liquids mix and leaves decompose. In fact, the natural tendency for systems to move from low-entropy states to high-entropy ones seems to be the only thing that reliably imbues the universe with a consistent temporal direction. Entropy engraves an arrow of time for processes that would otherwise just as easily happen in reverse.
The idea of entropy would ultimately extend far outside the confines of thermodynamics. “When Carnot wrote his paper … I don’t think anybody imagined what would come out of it,” said Carlo Rovelli, a physicist at the Aix-Marseille University.
Extending Entropy
Entropy experienced a rebirth during World War II. Claude Shannon, an American mathematician, was working to encrypt communication channels, including the one that connected Franklin D. Roosevelt and Winston Churchill. That experience led him to think deeply about the fundamentals of communication over the following years. Shannon sought to measure the amount of information contained in a message. He did so in a roundabout way, by treating knowledge as a reduction in uncertainty.

Claude Shannon, who has been called the father of information theory, understood entropy as uncertainty.
Estate of Francis Bello; Science Source
At first glance, the equation Shannon came up with has nothing to do with steam engines. Given a set of possible characters in a message, Shannon’s formula defines the uncertainty about which character will appear next as the sum of the probability of each character appearing multiplied by the logarithm of that probability. But if any character is equally probable, Shannon’s formula gets simplified and becomes exactly the same as Boltzmann’s formula for entropy. The physicist John von Neumann supposedly urged Shannon to call his quantity “entropy” — in part because it closely aligned with Boltzmann’s, but also because “no one knows what entropy really is, so in a debate you will always have the advantage.”
Just as thermodynamic entropy describes the efficiency of an engine, information entropy captures the efficiency of communication. It corresponds with the number of yes-or-no questions needed to figure out the contents of a message. A high-entropy message is a patternless one; without a way to guess the next character, the message requires many questions to be fully revealed. A message with a lot of patterns contains less information and is easier to guess. “It’s a very beautiful interlocking picture of information and entropy,” Lloyd said. “Entropy is information we don’t know; information is information we do know.”
In two landmark papers in 1957, the American physicist E.T. Jaynes cemented this connection by viewing thermodynamics through the lens of information theory. He considered thermodynamics to be a science of making statistical inferences from incomplete measurements of particles. When partial information is known about a system, Jaynes proposed, we should assign equal likelihood to every configuration that’s compatible with those known constraints. His “principle of maximum entropy” provides the least biased way of making predictions about any limited data set and is now employed everywhere from statistical mechanics to machine learning and ecology.
Notions of entropy developed in disparate contexts thus fit together neatly. A rise in entropy corresponds to a loss in information about microscopic details. In statistical mechanics, for instance, as particles in a box get mixed up and we lose track of their positions and momentums, the “Gibbs entropy” increases. In quantum mechanics, as particles become entangled with their environment, thus scrambling their quantum state, the “von Neumann entropy” rises. And as matter falls into a black hole and information about it gets lost to the outside world, the “Bekenstein-Hawking entropy” goes up.
What entropy consistently measures is ignorance: a lack of knowledge about the motion of particles, the next digit in a string of code, or the exact state of a quantum system. “Despite the fact that entropies were introduced with different motivations, today we can link all of them to the notion of uncertainty,” said Renato Renner, a physicist at the Swiss Federal Institute of Technology Zurich.
However, this unified understanding of entropy raises a troubling concern: Whose ignorance are we talking about?
A Whiff of Subjectivity
As an undergraduate physics student in northern Italy, Carlo Rovelli learned about entropy and the growth of disorder from his professors. Something didn’t sit right. He went home, filled a jar with oil and water, and watched the liquids separate as he shook it — a seeming departure from the second law as it had been described to him. “What they’re telling me is bullshit,” he recalled thinking. “It was so clear there was a problem in the way that things were taught.”
Rovelli’s experience captures a key reason why entropy is so perplexing. There are plenty of situations in which order appears to increase, from a child cleaning up their bedroom to a refrigerator cooling down a turkey.
Rovelli understood that his apparent triumph over the second law was a mirage. A superhuman observer with powerful thermal vision would see how the parting of oil and water releases kinetic energy to the molecules, leaving a more thermally disordered state. “What’s really going on is there’s macroscopic order forming at the expense of microscopic disorder,” Rovelli said. The second law always holds; sometimes it’s just out of sight.
Jaynes helped clarify this issue as well. To do so, he turned to a thought experiment first proposed in 1875 by Josiah Willard Gibbs, which became known as the Gibbs mixing paradox.
Suppose you have two gases, A and B, in a box, separated by a divider. When you lift the divider, the second law demands that the gases will spread out and mix, increasing the entropy. But if A and B are identical gases held at the same pressure and temperature, lifting the divider doesn’t change the entropy, as the particles are already maximally mixed.
The question is: What happens if A and B are distinct gases, but you can’t tell them apart?
Over a century after Gibbs posed the paradox, Jaynes presented a resolution (which he insisted Gibbs already understood but failed to articulate clearly). Imagine that the gases in the box are two different types of argon, identical except that one of them is soluble in a not-yet-discovered element called whifnium. Before the discovery of whifnium, there’s no way to tell the two gases apart, and thus lifting the divider initiates no apparent change in entropy. After whifnium’s discovery, however, a clever scientist could employ it to differentiate the two argon species, calculating that the entropy increases as the two types mix. Furthermore, the scientist could design a whifnium-based piston that harnesses previously inaccessible energy from the natural mixing of the gases.
What Jaynes made clear is that the “orderliness” of a system — and thus the potential to extract useful energy from it — depends on the relative knowledge and resources of an agent. If an experimenter can’t discriminate gases A and B, they are in effect the same gas. As soon as scientists have the means to tell them apart, they can harness work by exploiting the gases’ tendency to mix. Entropy depends not on the difference between the gases, but on their distinguishability. Disorder is in the eye of the beholder.

The physicist Carlo Rovelli has long emphasized the observer-dependence of quantities in physics, including entropy.
Christopher Wahl
“The amount of useful work that we can extract from any system depends — obviously and necessarily — on how much ‘subjective’ information we have about its microstate,” Jaynes wrote.
The Gibbs paradox emphasizes the need to treat entropy as a perspectival property rather than one inherent to a system. And yet, the subjective picture of entropy was difficult for physicists to swallow. As the philosopher of science Kenneth Denbigh wrote in a 1985 textbook, “Such a view, if it is valid, would create some profound philosophical problems and would tend to undermine the objectivity of the scientific enterprise.”
Accepting this conditional definition of entropy has required a rethinking of the fundamental purpose of science. It implies that physics more accurately describes individual experience than some objective reality. In this way, entropy has been swept up in the larger trend of scientists realizing that many physical quantities make sense only in relation to an observer. (Even time itself was rendered relative by Einstein’s theory of relativity.) “Physicists don’t like subjectivity — they’re allergic to it,” said Anthony Aguirre, a physicist at the University of California, Santa Cruz. “But there is no absolute — that’s always been an illusion.”
Now that acceptance has come, some physicists are exploring ways to bake subjectivity into mathematical definitions of entropy.
Aguirre and collaborators have devised a new measure they call observational entropy. It offers a way of specifying which properties a given observer has access to by adjusting how those properties blur, or “coarse-grain,” the observer’s view of reality. It then attributes equal probability to all microstates compatible with those observed properties, just as Jaynes proposed. The equation bridges thermodynamic entropy, which describes broad macroscopic features, and information entropy, which captures microscopic details. “This sort of coarse-grained, partly subjective view is the way we engage with reality in a meaningful way,” Aguirre said.
A number of independent groups have used Aguirre’s formula to hunt for a more rigorous proof of the second law. For his part, Aguirre hopes to use his measure to explain why the universe started out in a low-entropy state (and therefore why time flows forward) and to get a clearer picture of what entropy means in black holes. “The observational entropy framework provides much more clarity,” said Philipp Strasberg, a physicist at the Autonomous University of Barcelona, who recently included it in a comparison of different microscopic entropy definitions. “It really connects ideas from Boltzmann and von Neumann with what people do nowadays.”

Anthony Aguirre has defined a quantity he calls observational entropy that other researchers find clarifying.
Lisa Tse for FQxl
Meanwhile, quantum information theorists have taken a different approach to handling subjectivity. They are treating information as a resource that observers can use to interact with a system that’s increasingly blending together with its environment. For a supercomputer with unlimited power that could track the exact state of every particle in the universe, entropy would always remain constant — since no information would be lost — and time would cease to flow. But observers with finite computational resources such as ourselves always have to contend with a coarse-grained picture of reality. We can’t keep track of the motion of all the air molecules in a room, so we take averages in the form of temperature and pressure. We progressively lose track of microscopic details as systems evolve into more probable states, and this relentless trend materializes as the flow of time. “The time of physics is, ultimately, the expression of our ignorance of the world,” Rovelli wrote. Ignorance composes our reality.
“There’s a universe out there, and there’s a universe that each observer carries with them — their understanding and model of the world,” Aguirre said. Entropy provides a gauge of the shortcomings in our internal models. These models, he said, “allow us to make good predictions and act intelligently in an often hostile but always difficult physical world.”
Driven by Knowledge
In the summer of 2023, Aguirre hosted a retreat in the rolling foothills of a historic mansion estate in Yorkshire, England, through a nonprofit research organization he co-founded in 2006 called the Foundational Questions Institute, or FQxI. Physicists from around the world gathered for a weeklong intellectual slumber party complete with opportunities for yoga, meditation and wild swimming. The event rounded up researchers who had received grants from FQxI to investigate how to use information as fuel.

A scene from the FQxI retreat in Yorkshire.
Lisa Tse for FQxl
For many of these physicists, the study of engines and computers has become blurred. They’ve learned to treat information as a real, quantifiable physical resource — a diagnostic of how much work can be extracted from a system. Knowledge, they realized, is power. Now they’re setting out to harness that power.
One morning, after an optional yoga session in the estate’s yurt, the group heard from Susanne Still, a physicist at the University of Hawai‘i at Mānoa. She discussed new work that harkens back to a century-old thought experiment first proposed by the Hungarian-born physicist Leo Szilard.
Picture a box with a vertical divider that can slide sideways back and forth between the left and right walls of the box. There’s a single particle in the box, located to the left of the divider. As the particle ricochets off the walls, it will push the divider rightward. A clever demon can rig up a string and pulley such that, as the divider gets pushed by the particle, it tugs on the string and lifts a weight outside the box. At this point, the demon can sneakily reinsert the divider and restart the process — enabling an apparent source of infinite energy.
To consistently get work out of the box, however, the demon must know which side of the box the particle is in. Szilard’s engine is fueled by information.
In principle, information engines are sort of like sailboats. On the ocean, you use your knowledge about the direction of the wind to adjust your sails to propel the boat forward.
But just like heat engines, information engines are never perfect. They too must pay a tax in the form of entropy production. The reason we can’t use information engines as perpetual motion machines, as Szilard and others pointed out, is that it generates on average at least as much entropy to measure and store that information. Knowledge begets power, but acquiring and remembering that knowledge consumes power.
A few years after Szilard conceptualized his engine, Adolf Hitler became chancellor of Germany. Szilard, who was born into a Jewish family and had been living in Germany, fled. His work was overlooked for decades until it was eventually translated into English, as Still described in a recent historical review of information engines.
Recently, by studying the basic ingredients of information processing, Still has managed to expand and generalize Szilard’s concept of an information engine.
For over a decade, she has been working out how to treat observers as physical systems themselves, subject to their own physical limitations. How closely these limits can be approached depends not only on the data the observer has access to, but also on their data-processing strategy. After all, they must decide which properties to measure and how to store those details in their limited memory.
In studying this decision-making process, Still has found that collecting information that does not help an observer make useful predictions decreases their energy efficiency. She proposed that observers follow what she calls the “principle of least self-impediment” — choosing information-processing strategies that come as close as possible to their physical bounds in order to improve the speed and accuracy of their decision-making. She also realized that these ideas could be further explored by applying them to modified information engines.
In Szilard’s original design, the demon’s measurements perfectly reveal where the particle is located. In reality, however, we never have perfect knowledge of a system because our measurements are always flawed — sensors are subject to noise, displays have limited resolution, and computers have limited storage. Still showed how the “partial observability” that’s inherent in real-world measurements can be introduced with slight modifications to Szilard’s engine — essentially by changing the shape of the divider.
Imagine that the divider is tilted at an angle inside the box, and that the user can see only the horizontal position of the particle (perhaps they see its shadow projecting onto the box’s bottom edge). If the shadow is fully left or right of the divider, you know for sure which side the particle is on. But if the shadow is anywhere in the middle region, the particle could be either above or below the tilted divider, and thus either on the left or right side of the box.
Using partially observable information engines, Still computed the most efficient strategies for taking measurements of the particle’s location and encoding them in memory. This resulted in a purely physics-based derivation of an algorithm that’s also currently in use in machine learning, known as the information bottleneck algorithm. It offers a way to effectively compress data by preserving only relevant information.
Since then, with her graduate student Dorian Daimer, Still has investigated a number of different designs for the modified Szilard engines and studied the optimal encoding strategies in various cases. These theoretical devices serve as “fundamental building blocks of decision-making under uncertainty,” said Daimer, who has a background in cognitive science as well as physics. “That’s why studying the physics of information-processing is so interesting to me, because you go full circle in some sense and arrive back at describing the scientist.”
Industrializing Anew
Still wasn’t the only one in Yorkshire dreaming about Szilard engines. In recent years, a number of FQxI grantees have developed functioning engines in the lab in which information is used to power a mechanical device. Unlike in Carnot’s time, nobody expects these miniature engines to power trains or win wars; instead, they’re serving as test beds for probing fundamental physics. But just like last time, the engines are forcing physicists to reimagine what energy, information and entropy mean.
With Still’s help, John Bechhoefer has re-created Szilard’s engine with a silica bead smaller than a speck of dust floating in a bath of water. He and colleagues at Simon Fraser University in Canada trap the bead with lasers and monitor its random thermal fluctuations. When the bead happens to jiggle upward, they quickly raise the laser trap to take advantage of its motion. Just as Szilard imagined, they’ve managed to lift a weight by harnessing the power of information.

Susanne Still has modified Szilard engines to account for cases of uncertainty and partial information.
Mango Lime Studio
In investigating the limits of extracting work from their real-world information engine, Bechhoefer and Still have found that, in certain regimes, it can significantly outperform conventional engines. They’ve also tracked the inefficiency associated with receiving partial information about the bead’s state, inspired by Still’s theoretical work.
The information engine is now shrinking to the quantum scale with the help of Natalia Ares, a physicist at the University of Oxford who served on a panel with Still at the retreat. On silicon chips the size of a coaster, Ares traps a single electron inside a thin carbon wire, which is suspended between two pillars. This “nanotube,” which is cooled to within thousandths of a degree of absolute zero, vibrates like a guitar string, and its oscillation frequency is determined by the state of the electron inside. By tracking the nanotube’s minuscule vibrations, Ares and colleagues plan to diagnose the work output of different quantum phenomena.
Ares has a long list of experiments to probe quantum thermodynamics scribbled across chalkboards up and down the halls. “It’s basically all of the industrial revolution, but nano,” she said. One planned experiment takes after Still’s idea. It involves adjusting how perfectly the nanotube’s vibrations depend on the electron (versus other unknown factors), essentially providing a knob for tuning the ignorance of the observer.
Ares and her team are probing the limits of thermodynamics on the smallest scales — the motive power of quantum fire, in a sense. Classically, the limit for how efficiently the motion of particles can be transformed into work is set by Carnot’s theorem. But in the quantum case, with a menagerie of entropies to choose from, it’s much more complicated to determine which one will set relevant bounds — or how to even define work output. “If you have a single electron like we have in our experiments, what does it mean, entropy?” Ares said. “In my experience, we are still very lost here.”

Natalia Ares studies thermodynamics on the quantum scale in her lab at Oxford, where her custom hot-pink refrigeration chamber serves as a symbol of changing times.
Courtesy of Natalia Ares
A recent study led by Nicole Yunger Halpern, a physicist at the National Institute of Standards and Technology, shows how common definitions of entropy production that are usually synonymous can disagree in the quantum realm, again because of uncertainty and observer dependence. On this tiny scale, it’s impossible to know certain properties at the same time. And the order in which you measure certain quantities can affect the measurement outcomes. Yunger Halpern thinks we can use this quantum weirdness to our advantage. “There are extra resources available in the quantum world that are not available classically, so we can bend around Carnot’s theorem,” she says.
Ares is pushing these new boundaries in the lab, hoping to pave a path for more efficient energy harvesting, charging of devices or computation. The experiments may also provide insight into the mechanics of the most efficient information processing systems we know of: ourselves. Scientists aren’t sure how the human brain can perform immensely complicated mental gymnastics using only 20 watts of power. Perhaps the secret to biology’s computational efficiency also lies in harnessing random fluctuations at small scales, and these experiments aim to sniff out any possible advantage. “If there is some win in this, there’s a chance that nature actually uses it,” said Janet Anders, a theorist at the University of Exeter who works with Ares. “This fundamental understanding that we’re developing now hopefully helps us in the future understand better how biology does things.”
The next round of Ares’ experiments will take place in a hot-pink refrigeration chamber that dangles from the ceiling of her lab in Oxford. She jokingly suggested the makeover to the manufacturers a few years ago, but they cautioned that metallic paint particles would hamper her experiments. Then the company secretly brought the fridge to an auto shop to cover it in a flashy pink film. Ares sees her new experimental arena as a symbol of changing times, reflecting her hope that this new industrial revolution will be different from the last one — more conscientious, environmentally friendly and inclusive.
“It feels very much like we’re at the start of something big and wonderful,” she said.
Embracing Uncertainty
In September 2024, a few hundred researchers gathered in Palaiseau, France, to pay homage to Carnot on the 200th anniversary of his book. Participants from across the sciences discussed how entropy features in each of their research areas, from solar cells to black holes. At the welcome address, a director of the French National Center for Scientific Research apologized to Carnot on behalf of her country for overlooking the impact of his work. Later that night, the researchers gathered in a decadent golden dining room to listen to a symphony composed by Carnot’s father and performed by a quartet that included one of the composer’s distant descendants.
Carnot’s reverberating insight emerged from an attempt to exert ultimate control over the clockwork world, the holy grail of the Age of Reason. But as the concept of entropy diffused throughout the natural sciences, its purpose shifted. The refined view of entropy is one that sheds the false dreams of total efficiency and perfect prediction and instead concedes the irreducible uncertainty in the world. “To some extent, we’re moving away from enlightenment in a number of directions,” Rovelli said — away from determinism and absolutism and toward uncertainty and subjectivity.
Like it or not, we are slaves of the second law; we can’t help but compel the universe toward its fate of supreme disorder. But our refined view on entropy allows for a more positive outlook. The trend toward messiness is what powers all our machines. While the decay of useful energy does limit our abilities, sometimes a new perspective can reveal a reservoir of order hidden in the chaos. Furthermore, a disordered cosmos is one that’s increasingly filled with possibility. We cannot circumvent uncertainty, but we can learn to manage it — and maybe even embrace it. After all, ignorance is what motivates us to seek knowledge and construct stories about our experience. Entropy, in other words, is what makes us human.
You can bemoan the inescapable collapse of order, or you can embrace uncertainty as an opportunity to learn, to sense and deduce, to make better choices, and to capitalize on the motive power of you.
This work was supported by a fellowship with the MIP.labor. MIP.labor is hosted at Freie Universität Berlin and is funded by the Klaus Tschira Foundation. Quanta Magazine is an editorially independent publication funded by the Simons Foundation.



