Where Does Meaning Live in a Sentence? Math Might Tell Us.

Monica Almeida for Quanta Magazine
Introduction
Growing up, Tai-Danae Bradley had no love for math. In 2008, she entered the City College of New York, where she played for the basketball team and hoped to start a career in sports nutrition. She saw her math courses as a curricular hurdle that only geniuses could really excel in. “I’d have rather had all my teeth pulled than do it for a living,” she said.
But in her sophomore year, her calculus professor changed her mind. Mathematics, she learned, was the language that all the sciences are written in. “There’s something deeper out there than what’s in the textbooks,” she said. “It’s a really delightful world that we live in, and mathematics is a way to see some of that.”
She quit the basketball team and decided to double-major in math and physics. Now, as a researcher at the artificial intelligence company SandboxAQ, and a visiting professor at the Master’s University in California, Bradley is using the language of math to try to better understand language itself.
Her lens is category theory, a way of stepping back from the specifics of any individual field in favor of a broader underlying framework that bridges all of them. By thinking of language as a mathematical category, she’s been able to apply established tools to study it and glean new insights.
Linguists hope her model can help them to prove certain theories about how grammar and meaning emerge from strings of words, and to identify how AI-generated text differs from human language. Bradley herself is more interested in how studying language in this way might allow her to develop new mathematical tools.
Quanta spoke with Bradley about how mathematics can inform the study of language and vice versa. The interview has been condensed and edited for clarity.
What is the question that got you started on this research path?
I was interested in understanding: What is the mathematical structure of language? What are its basic units? How do the mathematical relationships between words and phrases lead to meaningful content?
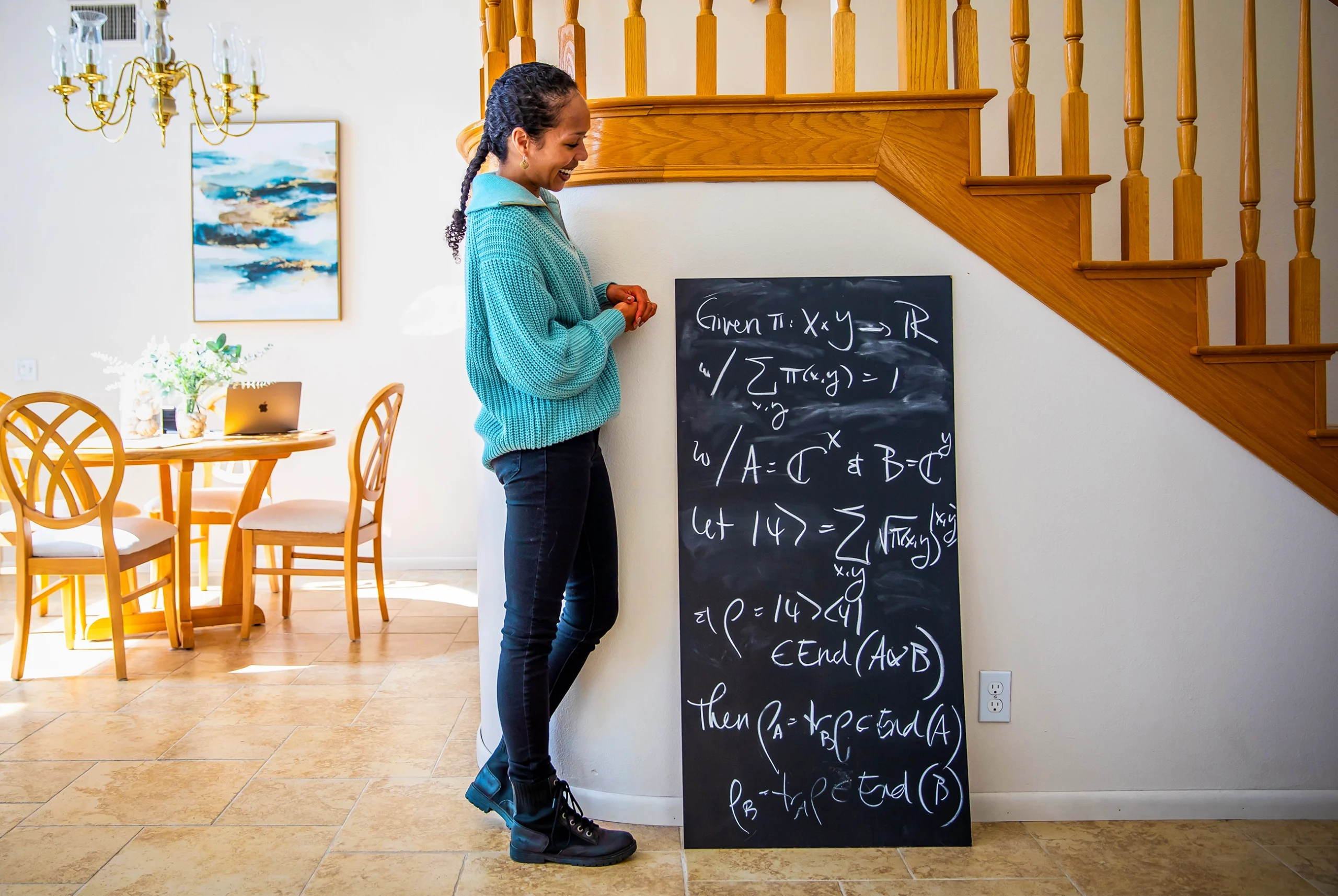
Tai-Danae Bradley disliked math as a child. But as an undergraduate, she began to appreciate how connected math is to the world around us.
There are many different ways to study language mathematically. You can think of language as having algebraic structure, for instance. When I multiply two numbers, I get another number. In the same way, I can “multiply,” or combine, two phrases in English and get another one.
You can also think of language in terms of category theory.
What is category theory?
A category consists of some objects, together with relationships between them, called morphisms. The objects could be sets, or groups, or vector spaces. The morphisms relate one object to another. Say your objects are sets. Then a morphism is a function that maps one set to another.
I like to think of category theory as Mad Libs for mathematics. In Mad Libs, you have one story, but you get different versions of the story based on the different words you fill in. It turns out that there are certain stories or constructions that are shared across the mathematical landscape. Different branches of math might use different words for things — like “group” instead of “vector space” — but when you swap out words in the right way, you can see that the underlying framework or story is really the same.
When I first learned some category theory in graduate school, I thought it was just the worst. I remember thinking, this is why people don’t like math. It’s abstraction for abstraction’s sake, with no basis in intuition. It was frustrating. It was only later that my Ph.D. adviser, John Terilla, helped me see what a powerful tool category theory can be.
What makes it so powerful?
It lifts your feet off the ground and gives you a bird’s-eye view of the mathematical landscape, so you can see connections that are imperceptible at the ground level. Now it’s one of the things I enjoy thinking about most — it just took more mathematical context and maturity to see it.

Bradley sees category theory at work all around her. She’s particularly interested in using it to understand language.
Monica Almeida for Quanta Magazine
What’s something category theory lets you see that you can’t otherwise?
A really meaningful question in mathematics is: When are two things the same? What does “same” mean, and how does it change depending on the kind of math you’re talking about?
For example, a set is kind of like a bag of marbles: It has no real structure to it. So we say two sets are the same when they have the same number of elements. A group, on the other hand, is a set whose elements interact through certain rules. Now your notion of sameness has to account for that extra structure.
Category theory provides a common template for describing these different notions of sameness. You can then use that template to jump between these different contexts when trying to solve a problem.
Can you give an example of this?
One of my favorite examples comes from the world of topology. Shapes called topological spaces form a category. You can stretch one into another, and this stretching is the morphism that relates them to each other.
Say you have two topological spaces, and you want to know if they’re the same. If they are, then when you stretch one space into the other, the number of holes it has doesn’t change. Dealing with these spaces directly can be super hairy, so this might be really difficult to figure out.
But that number of holes is always the same as a number that comes from a totally different category.

“Maybe studying language,” Bradley said, “will help us uncover some new mathematical structure that we just haven’t found yet.”
Monica Almeida for Quanta Magazine
Category theory lets you jump from the category of topological spaces to this other category. You can use something called a functor to translate your two topological spaces into vector spaces, for example. If you then find that the dimensions of the vector spaces are different — something that’s much easier to measure — then you know the two spaces can’t be the same. And you figured this out by passing between the realms of topology and linear algebra using category theory.
So how do you use category theory to understand language?
Language and category theory go hand in hand. We don’t want to impose any particular rigid mathematical model onto language. We can start with simple frequencies, like how many times the word “cat” appears next to certain other words. If I say “Curiosity killed the ____,” I can calculate the probability that the next word is going be “cat” and not “helicopter.”
We can then think of every possible word or phrase (or combination of letters, really) as the objects in a more general kind of category called an enriched category. And every object is related to every other object by the probability that it will follow it — these are the enriched versions of your morphisms. You can think of them as arrows between words, each labeled with a number.
Why is it helpful to frame language in terms of categories like this?
If you love something, you begin to see it everywhere. Because it’s so abstract, and because it connects ideas across mathematics, many things that are familiar to mathematicians can be re-expressed in terms of category theory.
But it goes deeper than that. Once you think of language as a category, you have access to decades of constructions that people have developed. So you can just flip through this recipe book and find some that may be helpful for studying human language, or for understanding what’s going on in large language models.
How have you used one of these recipes to understand something new?
One thing people are wondering is how you can get more abstract concepts just starting from basic information about how words tend to be combined. If I ask ChatGPT to list five reptiles that are also household pets, how does it know how to join those two things? How do you go from strings of symbols and their statistics to this kind of logical relationship?
We can use one of our recipes to give us potential insight into this. First, we associate to every word a category-theoretic construction that captures every phrase that word can appear in, and how commonplace that phrase is. We can then take the constructions associated to two different words and perform some very simple operations on them — operations that are again very classical in category theory.

In order to make mathematics more accessible to others, Bradley runs a popular blog called Math3ma.
Monica Almeida for Quanta Magazine
And what we get is a construction that automatically relates the two original words. If our original words were “big” and “yellow,” we get something that, roughly speaking, assigns large numbers to probable phrases like “big yellow sun,” and smaller numbers to phrases like “big yellow ruby.” This simple operation from category theory gives you something that’s actually linguistically meaningful — a way of combining words to build up a more general concept, like the concept of things that are both big and yellow.
So using category theory, you can show — mathematically — how higher-level concepts can potentially emerge from really simple statistical information. I think it’s a clue that maybe this is how ideas are formed. I don’t want to say “formed in the human mind,” because who knows how the brain works. But this conceptual content is there in the raw data of how language is used, because all we started from is those frequencies.
And you think this could be what LLMs are doing?
I joined this research project before LLMs took over. But they start from the same frequencies we did. I don’t know what’s actually happening inside transformers. I’m not sure anybody does. But maybe this can be a conversation starter.
What does your work imply about language more generally?
I think it indicates that there is meaningful information in just bare-bones syntax, like what goes with what. If you look at which words tend to come after “blue” — like “blue marble” or “blue sky,” but not “blue avocado” — can you get a sense of what the word “blue” means?
In the linguistic community, that’s not an agreed-upon fact. As a human, I can get meaning out of a sentence on the page, but words on paper aren’t all I have access to. I have access to the world. Linguists have debated over whether you need a world model to extract meaning from written language. The idea that meaning lives in the arrangement of words is an old one in linguistics, but it’s largely fallen out of fashion in recent decades.

Bradley thinks her work “indicates that there is meaningful information in just bare-bones syntax, like what goes with what,” she said.
Monica Almeida for Quanta Magazine
But this work — and the recent success of LLMs — supports the idea that there is meaning in the statistics of how words are used together. So it might contribute to this larger conversation that linguists are having.
In your most recent paper, you also use category theory to bring entirely new concepts into the study of language.
Right. We were studying what’s called the magnitude of a category — a sort of measure of size that’s related to topology, and that characterizes the category. My co-author Juan Pablo Vigneaux recently figured out a new way to compute magnitude. So we decided to try it on the category formed by language, after some additional work.
And surprisingly, when we worked out what this formula for magnitude would look like for the category, we ended up with a mathematical expression that contained a central quantity found in information theory. Entropy — a measure of how much information something contains.
What does this connection tell you?
It points to an intriguing connection between entropy and topology. These things do not normally talk to each other — they’re on totally different ends of the scientific landscape. But this connection has started to pop up in recent years, and this might be another example. I’m very interested in this phenomenon where things that feel different turn out to be fundamentally related.
We’re also staring at the answer like, “Whoa, what is this?” What does entropy mean in the context of language? What might that tell us? Could computing magnitude then be used as a way to compare the structures of different languages, for instance — or to compare human language to LLM-generated language?
This feels like just the first rung in a very tall ladder. There’s much more to do.
Where are you hoping your work will take you?
I’m hoping it can bring us to a deeper understanding of mathematics itself.
It can teach us about the phenomenon of language, so we can understand the world around us better. But what is really cool is that maybe there’s some mathematical ideas that are missing, and that’s why this phenomenon is so mysterious and hard to understand.
Maybe studying language in this way will help us uncover some new mathematical structure that we just haven’t found yet. This happens all the time in math. Mathematicians come across things that don’t have a name yet, structures that are there for the taking.
I think in five years, we might have new mathematical ideas that were inspired by language.



