A Brief History of Tricky Mathematical Tiling

James O’Brien for Quanta Magazine
Introduction
Every day we see examples of repeating motifs. This symmetry and regularity can seem mundane and almost invisible, as with brickwork on building walls or the hexagonal pattern in a honeycomb. Or if we’re lucky enough to encounter something like the elegant tile work in Spain’s Alhambra or M.C. Escher’s creative drawings, the patterns can inspire and amaze us.
For centuries, mathematicians have played with these repeating shapes, wresting fascinating insights and novel possibilities from them. The beauty of the mathematics rivals the beauty of the designs themselves.
The simplest tilings are made of identical polygons with sides of equal length and angles of equal measure joined full edge to full edge. But although there are infinitely many of these “regular” polygons — one for each number of sides — there are only three regular tilings, formed from shapes with three, four or six sides — that is, triangles, squares and hexagons.
The other shapes just aren’t built for it. A regular pentagon (with five sides) has an interior angle of 108 degrees. This doesn’t evenly divide into 360 degrees, so any attempt to assemble regular pentagons into a tiling is bound to produce gaps that can’t be filled; we say that the regular pentagon cannot tile the plane. And regular polygons with more than six sides have interior angles too large for three to meet at a single point, and so they cannot either.


The three regular tilings of the plane.
Another take on tiling with regular polygons comes from Johannes Kepler, today best known for his discoveries about planetary motion. In 1619, he showed that even if you use more than one regular polygon, you can create only eight new tiling patterns where the configuration around each vertex is identical. (If we’re allowed to stray from this restriction, there are more possibilities.)

A semiregular tiling of the plane.
When we allow irregular polygons, things get more interesting. Surprisingly, every triangle can tile the plane, and even more surprisingly, so can every quadrilateral.
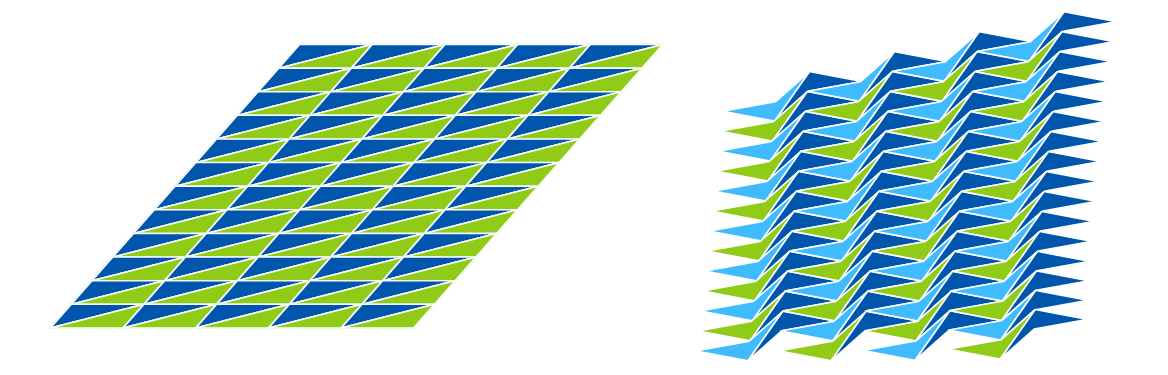
Every triangle and every quadrilateral can tile the plane.
On the other hand, it’s impossible to tile the plane with any convex polygon of more than six sides; the sum of the interior angles is just too large. So that leaves only pentagons and hexagons as remaining possibilities.
In his 1918 doctoral thesis, Karl Reinhardt proved that it’s possible to tile the plane with infinitely many convex hexagons — those without indentations — which he grouped into three families.
Convex pentagons that tile the plane were trickier to classify. Reinhardt discovered five families of such pentagons; 50 years later, Richard Kershner found three more. Then in 1975, Martin Gardner wrote about the problem for Scientific American, bringing it to the attention of professional and amateur mathematicians alike. One such amateur, a computer programmer named Richard James III, sent Gardner an example of a ninth family, asking, “Do you agree that Kershner missed this one?” He had.
Marjorie Rice, a homemaker, also read Gardner’s column and began to puzzle away at the problem at her kitchen table. She tinkered for over two years and discovered four more families of tiling pentagons.
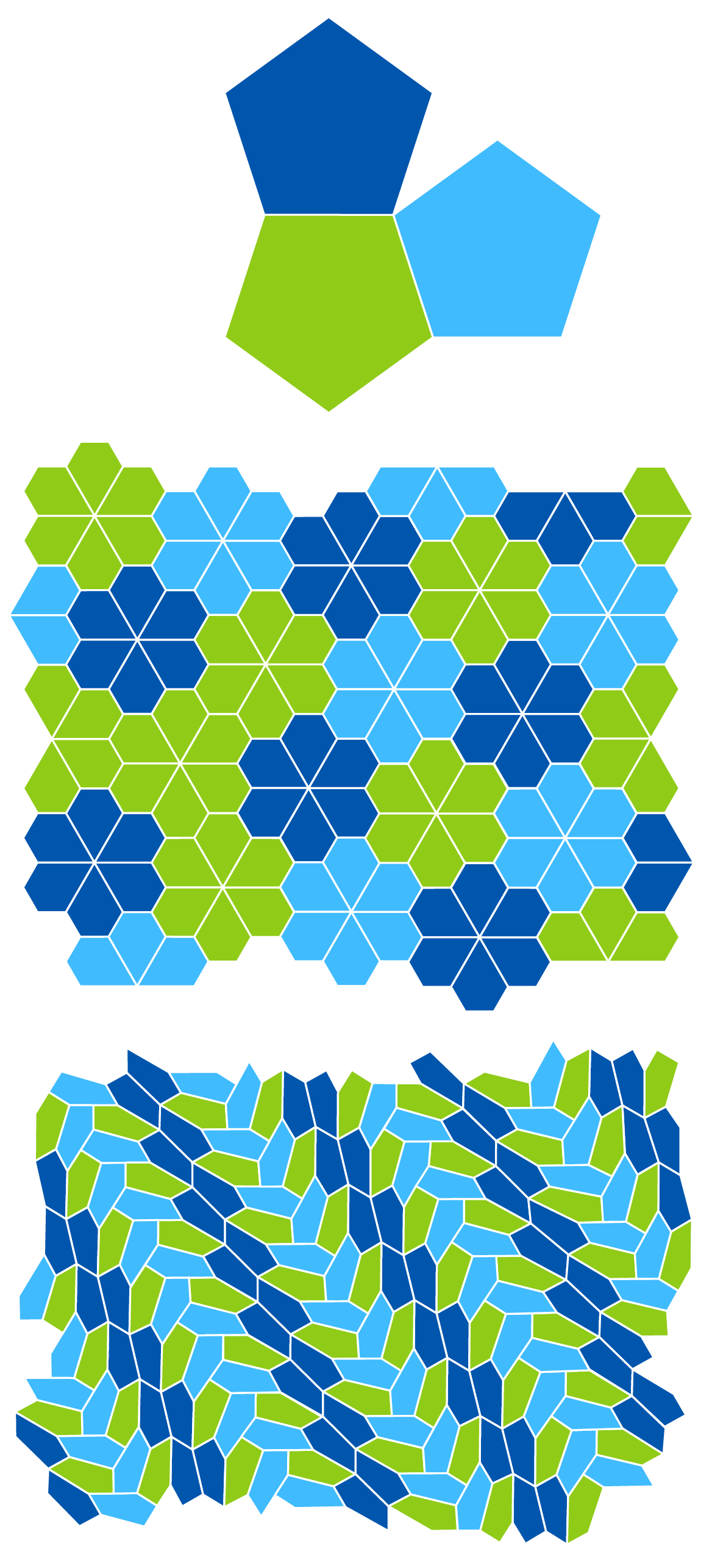
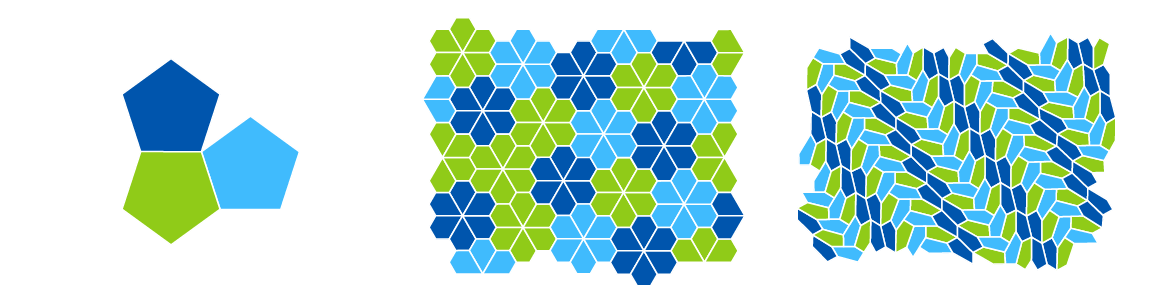
Regular pentagons do not tile the plane, but there are 15 families of irregular convex pentagons that do.
Researchers found a 14th family of tiling pentagons in 1985, and three decades later, another team found a 15th family using a computer search. No one knew if this discovery completed the list, or if there were more families still hiding. That question was answered in 2017 when Michaël Rao proved that all convex tiling pentagons — and with them, all convex tiling polygons — had been found.
All these tilings repeat. That is, they have a periodic symmetry, which basically means that if we were to trace the tiling on a piece of paper and slide that paper in certain directions, it would line up exactly with the tiling again.
Other kinds of symmetries are also possible. For example, a mirror symmetry implies that our patterns will line up if we flip our tracing paper upside down about a fixed line. Rotational symmetry means that they’ll line up if we rotate our paper. And we can combine actions to obtain a glide reflection symmetry, which is like sliding the paper and then flipping it over.
In 1891, the Russian crystallographer Evgraf Fedorov proved that there are only 17 ways that these symmetries can be combined. Since this restriction applies to all periodic decorations of the plane, these are widely referred to as the 17 “wallpaper groups.”
Once one is familiar with this classification of symmetry patterns, it is nearly impossible to see a periodic design, however intricate, and not view it as a puzzle to decode: Where and how, exactly, does it repeat? Where are those symmetries?
Of course, not every tiling design is periodic. It is possible, and often easy, to place tiles in the plane so that the resulting design never repeats. In our example with hexagons, squares and triangles, you can do this by simply rotating a single hexagon and the polygons surrounding it by 30 degrees. The resulting tiling no longer has translational symmetries.
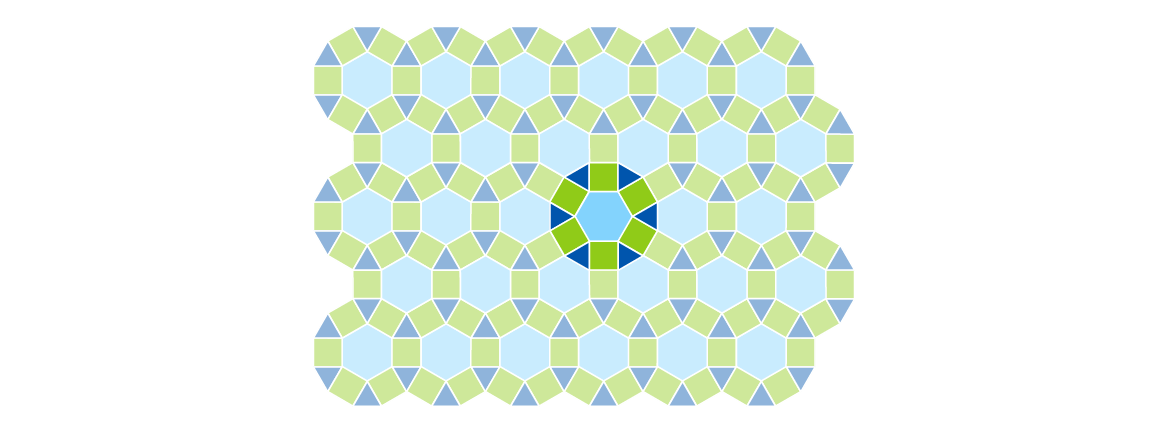
This tiling is not periodic.
In 1961, the logician Hao Wang conjectured that if a set of shapes tiles the plane, then the shapes must be able to tile the plane periodically. Just a few years later, his graduate student Robert Berger proved him wrong by discovering a massive set of over 20,000 tiles that tile the plane, but only nonperiodically. Such tile sets are called aperiodic.
Although Berger and others were able to bring down the size of these aperiodic sets significantly, in the mid-1970s Roger Penrose captured the world’s attention by discovering very small sets of his own aperiodic tiles. The smallest sets require just two tiles.

Roger Penrose’s aperiodic tiles. Left: Rhombuses, or “rhombs.” Right: Kites and darts.
These shapes and patterns enthralled mathematicians, scientists and the general public. But they did raise an obvious next question: Is there a single aperiodic tile? The ultimate quest of tiling theory was now to find such an “einstein” tile — named not after the physicist, but for the German phrase “one stone.”
In 2010, Joshua Socolar and Joan Taylor came very close to discovering an einstein. The problem with their approach was that their tile had to be disconnected; this would be like tiling the plane with shapes like the state of Hawai‘i, a single entity consisting of separate regions, rather than with connected shapes like California. Increasingly, mathematicians suspected that if an einstein did exist, it would have to be something very geometrically complicated.
In March 2023, an amateur shocked the world again. A retired print technician and mathematical hobbyist named David Smith had discovered not just one aperiodic monotile, but an infinite family of these elusive einsteins. He looped in Craig Kaplan, Chaim Goodman-Strauss and Joseph Samuel Myers — experts in computer science, mathematics and the theory of tilings — and together they presented a geometrically simple einstein called the hat tile (which the internet thought looked like a T-shirt).
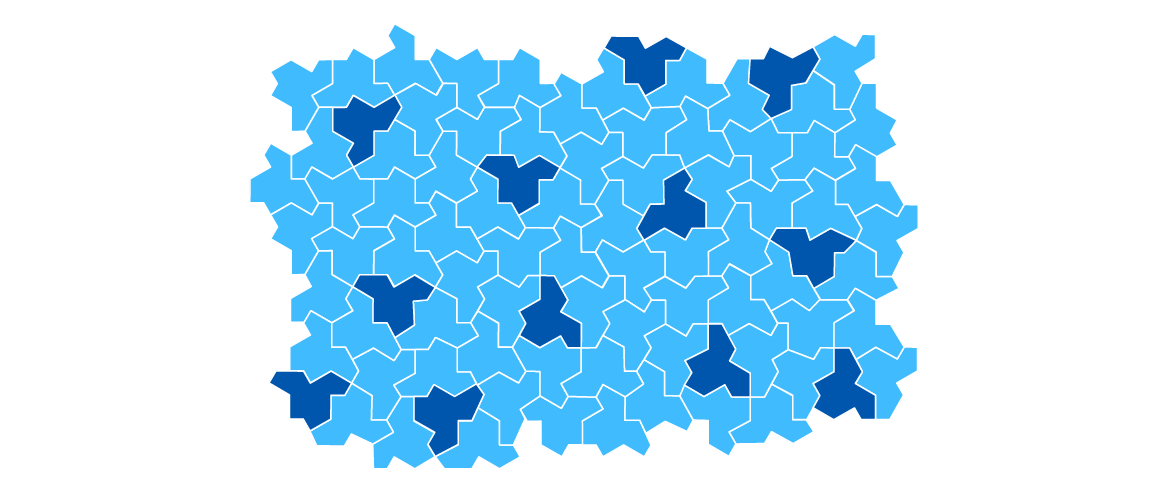
The aperiodic hat tiling. The dark blue hats are reflected versions of the light blue ones.
The reaction was swift and positive. The discoverers spoke at conferences and gave talks online. Mathematical artists leaped at the chance to find creative ways to produce Escher-like designs based on these new geometrically interesting tiles. The hat tile even appeared in the monologue of one late-night television show.
Yet there was still room for improvement. To tile the plane with the hat, you have to flip approximately one-seventh of the tiles upside down. A homeowner wanting to tile their bathroom with the hat tile would have to buy two types of tiles: a standard tile and its mirror image. Was this really necessary?
Even before the excitement of the hat tile had died down, the team made another announcement. Smith had found, in that infinite family of aperiodic monotiles, one that he called a “spectre” that could tile the plane without requiring reflected copies. A true einstein had finally appeared.
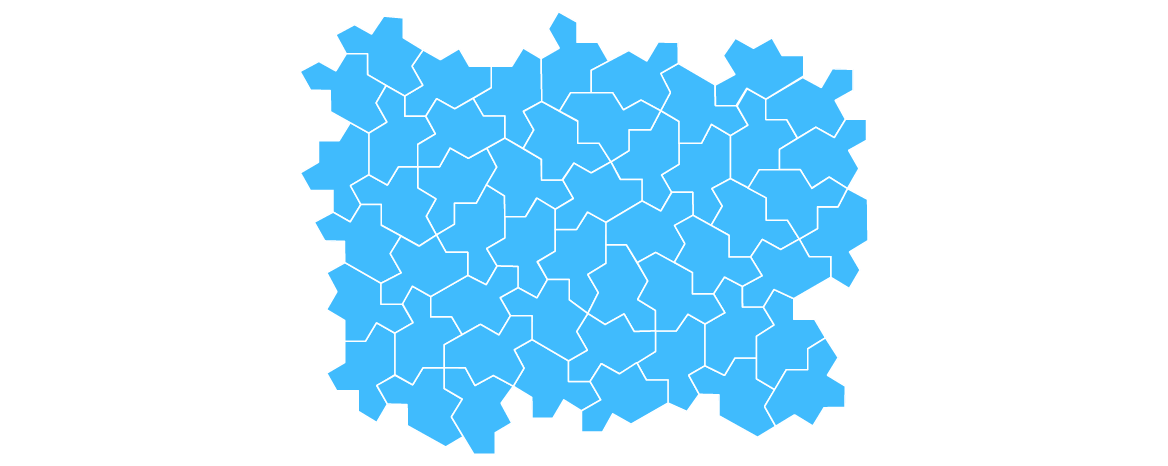
The spectre monotile tiles the plane without reflections.
We are now in the midst of a resurgence in the mathematical exploration of tilings and tessellations. It has relied on important contributions from amateurs, inspired the creativity of mathematical artists, and harnessed the power of computers to push the boundaries of knowledge forward. And from it, we have achieved new insights into the nature of symmetry, geometry and design.
Correction: October 30, 2023
The original version of this article stated that it is impossible to tile the plane with any polygon of more than six sides. This is true only if the polygon is convex.