A Universal Law for the ‘Blood of the Earth’

A river’s path is governed by an uncountable number of factors. But universal patterns have been found.
Introduction
About five centuries ago, Leonardo da Vinci surveyed the Arno River, likely for a scheme — devised with Niccolò Machiavelli — to divert the strategically important waterway from Pisa to Florence. Their grand plan never went forward. But at some point in the process, da Vinci envisioned what the entire hydrological system would look like from above.
He sketched the Arno’s main stem, which split into upstream branches. Then those branches themselves branched, and so on, fanning out into small spidery veins that fed the entire network. To da Vinci, this patterning looked suspiciously alive. River networks, he wrote, were a separate circulatory system, one that carried the “blood of the Earth.”
Today, branching river networks still lure would-be explainers, many of whom hope to glimpse some underlying mathematical code responsible for etching out these common patterns. It’s no easy feat. Geomorphologists have long measured statistical laws that river networks seem to obey — the longest stream snaking through a basin, for example, seems to be proportional to the area of the basin raised to the power of 0.6. But these generic laws haven’t offered much insight into what actually shapes the networks.
Another problem is that the real world doesn’t skimp on detail. The amount of rain, the nooks and crannies that the rain falls into, the exact sediments that start to erode, the trees that line channel banks, and the water table rising from below all vary across place and time. And they all might matter.
Yet recently, one fundamental recipe for building river networks has begun to take shape. A team led by Daniel Rothman, a geophysicist at the Massachusetts Institute of Technology, has spent the past few years arguing that a basic, near-ubiquitous growth pattern can explain the shapes of river networks carved into wet soils — and maybe beyond.
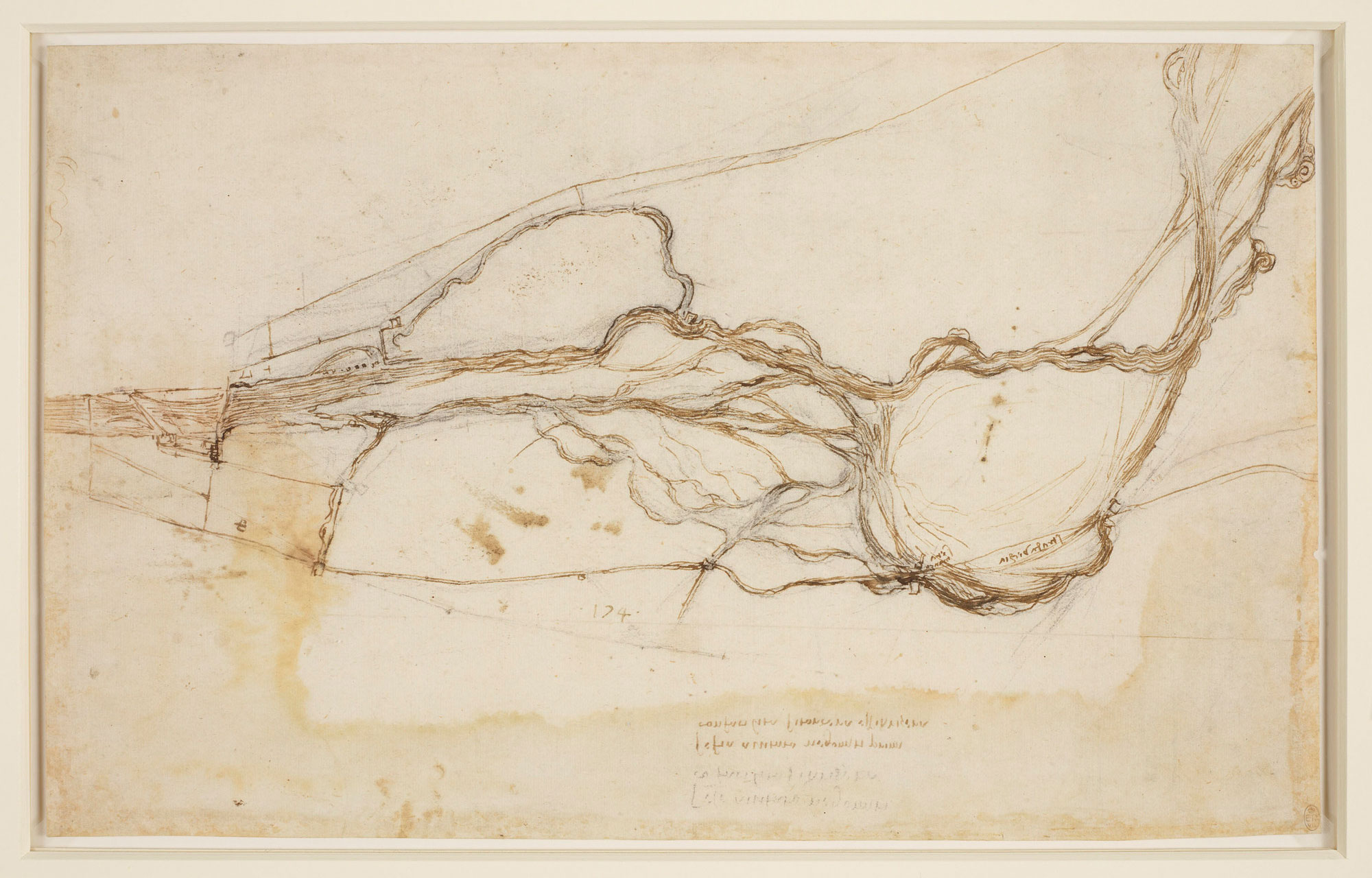
In 1504 Leonardo da Vinci sketched the Arno river west of Florence as part of a study of how it might be diverted.
They’ve taken their model past the chalkboard, out into the field and, more recently, across the tumultuous, noisy totality of Earth’s river basins. Now they’re looking even farther afield to Mars, and perhaps Saturn’s moon Titan, each of which hosts its own mysterious branching channels. Their basic math doesn’t work all the time, but it does work widely. And where it doesn’t work, the team believes, that breakdown provides its own hint to underlying environmental conditions.
Beyond all that, their recipe for river networks also offers a certain aesthetic quality. “The mathematics is beautiful,” said Christopher Paola, a geologist at the University of Minnesota, who was not part of the research. “It’s just gorgeous.”
From Bump to Branch
If Rothman is right, his team’s work would add river networks, or at least some of them, to a class of eerily similar branching patterns found throughout nature. These systems all follow what mathematicians call Laplacian growth, named for the 18th-century French mathematician Pierre-Simon Laplace. Snowflakes, analyzed up close, seem to sprout their symmetric-looking crystalline structures through Laplacian growth. The process also predicts the branching pattern that electric current takes when it leaps across a gap, how bacterial colonies spread in petri dishes, and how minerals grow into veiny, dendritic patterns that look like fossils in rocks around the world.

In each, patterns grow when a bump develops from an imperfection on an otherwise smooth boundary. Consider the surface of a newborn snowflake, a frozen edge creeping out into unfrozen ambient water. Invariably, what starts out as a smooth edge will have some little bump on it — even just a few out-of-place atoms. That bump will jut a little bit into the liquid. Out there, the bump loses heat to the surrounding water a little faster. It cools, and a bit more water freezes on top of it. In time the bump grows, forming a bigger bump. The process continues, and soon enough the atomic imperfection extends into a crystalline branch.
The details vary in different Laplacian systems, but the rule is the same: Growth begets growth. Bumps make branches. Branches keep growing at their tips. Eventually, the branches may spawn their own bumps through the same process. That can make new branches that copy the same shapes as their parent branches, only at smaller scales.
Rothman’s team has long argued that certain river networks — the granddaddy of all obvious natural branching patterns — belong to this illustrious group. But the rub, for pattern hunters, is to show that simple rules really do carry over into messy reality.
A River Grows
Rothman’s group found their proof of concept near the town of Bristol in the Florida Panhandle. There, a vast network of channels feeds water into the Apalachicola River.
The network itself, ending in dendritic channel tips, is slowly extending away from the river. As the channel tips grow, they cut into 2-million-year-old sand. At each growing tip, groundwater burbles to the surface. Just like the cold water around a growing snowflake, it’s the kind of environment that lends itself to Laplacian growth.
Building on work on groundwater-driven erosion by Thomas Dunne, a geomorphologist at the University of California, Santa Barbara, the Rothman team set out to test whether simple math could describe this situation. They flew to Florida and sloshed through these streams, measuring the rate at which water flows through individual channels. Then they used ground-penetrating radar to check the height of the water table below.

Tributaries of the Apalachicola River in Florida demonstrate a remarkable statistical consistency.
Source: USGS
They then set out to compare the real scene to the detailed theoretical predictions they’ve sketched out over the past few years.
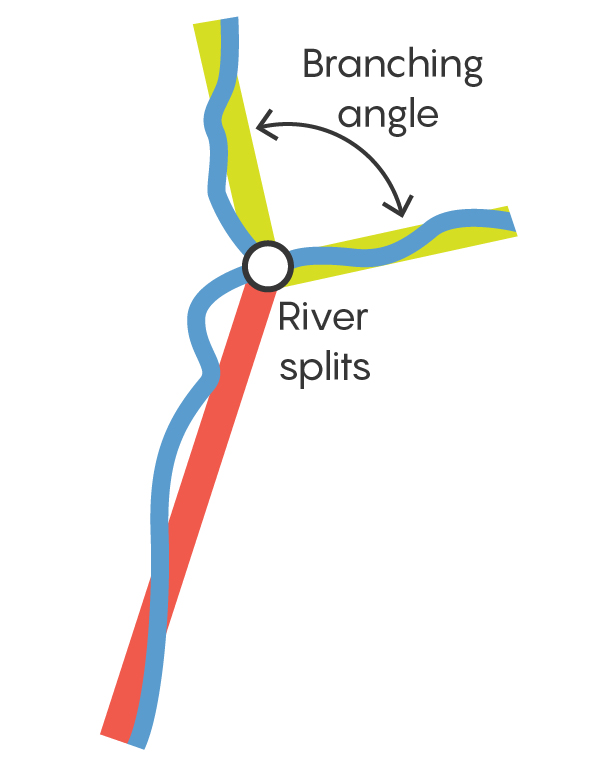
So far, they have predicted and checked details like the rounded shapes of valley heads, the directions they grow in, and, in a paper published just this summer, the way branches scale with the size of the basin containing them. But perhaps their most far-reaching result addresses a simple question: At what angles do streams branch?
The logic of Laplacian growth provides an answer. Imagine zooming in close to the tip of a single growing channel. Here, groundwater flows into the channel from multiple directions. As it does, the water pulls sand grains along with it. “You can go down and watch it,” Rothman said. “One sand grain at a time is leaving the spring.” Each missing grain extends the channel a little bit.
Source: DOI: 10.1098/rsta.2012.0365
The team’s current reasoning holds that the stream grows in the direction from which it attracts the most groundwater flow. If more water gushes in from the right side of the channel head, for example, the channel turns right. Soon, it points in the direction that makes the groundwater flowing to it symmetric, where it receives the same amount of water from either side.
Now imagine that one stream splits into two, with each new tip still finding the direction that draws the most groundwater flow. Competing effects determine the angle of the split. If the angle were wide, each new tip would bend inward, back toward the direction that maximized groundwater flow into the parent stream. And if the angle were narrow, the two tips would suck away each other’s groundwater, causing them to bend outward.
Instead, the two branches grow at a happy medium. The math of Laplacian growth predicts that the angle between the two should be 72 degrees, exactly one-fifth of the way around a circle. (The team later realized that physicists had encountered the same angle in the early 2000s while contemplating other Laplacian systems.)
And then reality played along. Rothman and team members Olivier Devauchelle, Alexander Petroff and Hansjörg Seybold found where streams in the intricate Florida network forked into two branches, at scales from large to small. Then they measured the angle of each junction.
Over 4,966 branches, their analysis showed, the junction angle averaged 71.9 degrees. “This is so close that one could almost believe,” said Seybold, now at the Swiss Federal Institute of Technology Zurich.
Florida or Something Fundamental?
But Florida, as it so often is, might just be its own special case. Yes, Laplacian growth appears to explain the patterning of one stretch of river in the Panhandle. But what about the world’s other rivers?
After Florida, the MIT group looked for their branching angle writ large, in a U.S. Geological Survey database of all decent-size streams across the continental U.S. They found it again. Branching angles vary widely, but for about half the country, they cluster around 72 degrees. And this June, Seybold extended the analysis still further, showing that the angle shows up across the globe. It works just as well in locations like the Amazon rainforest (where French Guiana borders Suriname) as it does in Vermont.

Simulations of Laplacian growth demonstrate how similar structures can emerge at many different size scales.
“I never imagined the results that we’d obtain would be ostensibly applicable to half the drainage networks on the planet,” Rothman said — “the wet half.”
The wetter the area, these studies show, the more branching angles seemed to approach 72 degrees. This could be because groundwater tables are highest in the most humid regions, and the same groundwater-powered mechanism found in the Florida Panhandle might exert some control.

Daniel Rothman, a geophysicist at the Massachusetts Institute of Technology.
John M. Hayes
Other geomorphologists need more convincing. They buy the case in Florida, where Rothman’s team nailed down the area’s idiosyncrasies. But they’re more skeptical of the argument that branching angles suffice to show the same fundamental growth process is super widespread. “My feeling is that the system in Florida is a very special system,” said Alan Howard, a geomorphologist at the University of Virginia.
In the 1980s Howard studied and simulated groundwater sapping out of sandstone in the southwestern U.S., eroding the rocks as it left them. “The drainage patterns looked very much like what they get in sand,” he said. But both the sand and sandstone networks have something rare in common. They occur in places where groundwater dominates.
Outside of these water-soaked landscapes, geomorphologists traditionally hold that surface water from precipitation, not groundwater, sculpts most river networks. In rare cases where groundwater dominates, sure, Laplacian growth might work. But elsewhere the mechanism doesn’t quite make sense.
“I don’t think anybody thinks — maybe, outside of that group — that those river networks in the rainiest places on Earth were formed by groundwater rather than rainfall,” said Michael Lamb, a geologist at the California Institute of Technology.
Paola, for his part, points back to the common branching angle. “72 degrees isn’t magic,” he said, acknowledging that idiosyncratic local details might also make it work. “But it seems to me,” he said, “there’s enough in the beautifully simple general theory that Dan’s group has come up with to make it work in a surprising large number of cases.”

Ancient streams appear to have carved channels into Jezero Crater on Mars, the recently announced landing site of NASA’s Mars 2020 rover.
Also interesting are the exceptions. In arid places like New Mexico, networks branch narrowly, at around 45 degrees. That second angle “took me a long time of trying and failing” to explain by theory, Seybold said. They still haven’t solved the specific angle, but the team argues that in arid regions, occasional surface runoff carves steeper channels with narrower junctions.
That then opened up a new possibility. If wet climate might brand river networks with the 72-degree signature of Laplacian growth, could that signature’s absence also reveal the existence of a different kind of climate?
Rivers on Mars
In the same June study that looked across Earth’s river basins, Seybold’s team also searched farther afield. They looked at remote sensing data from Mars, hoping that branching angles would hint at the Red Planet’s long-mysterious ancient climate.
In the 1970s, Viking orbiters first found branching valley networks etched into Mars. Current cold temperatures and low pressures don’t let surface water last very long there, so geomorphologists wondered whether the valleys could have been eroded by groundwater. “In my mind, we’ve come full circle,” Lamb said.
The Martian valleys showed narrower angles, like those in arid places like the southwest U.S. Consistent with other recent studies, the new work suggests that the ancient Red Planet was a relatively arid place. Perhaps occasional downpours carved the Martian valleys, not groundwater.
So while Laplacian growth might sculpt some — or maybe many — of the branching river patterns that have enticed scientists for centuries, for now, at least, other networks are still holding on to their secrets.