How Noether’s Theorem Revolutionized Physics
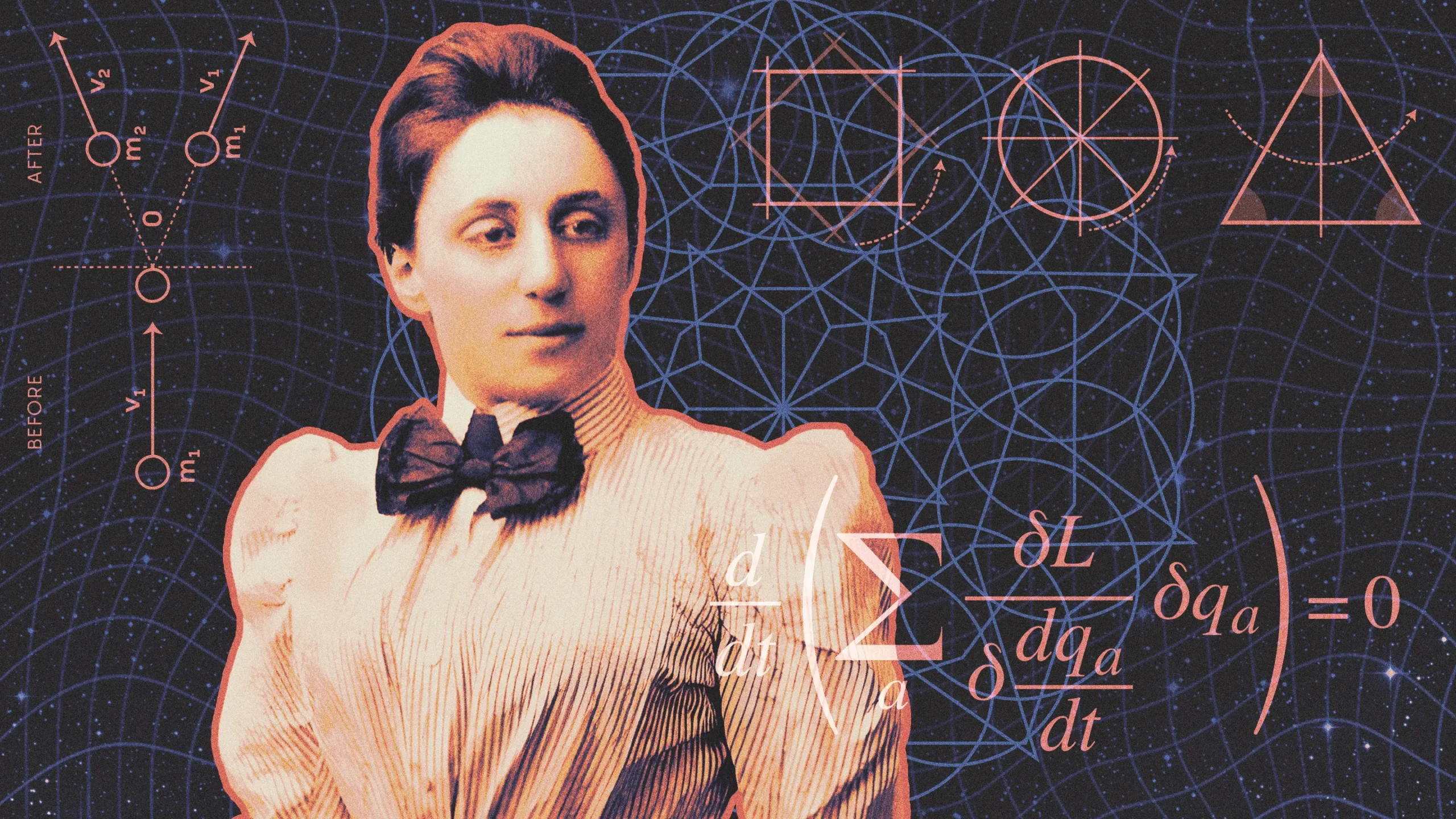
Kristina Armitage/Quanta Magazine
Introduction
In the fall of 1915, the foundations of physics began to crack. Einstein’s new theory of gravity seemed to imply that it should be possible to create and destroy energy, a result that threatened to upend two centuries of thinking in physics.
Einstein’s theory, called general relativity, radically transformed the meaning of space and time. Rather than being fixed backdrops to the events of the universe, space and time were now characters in their own right, able to curve, expand and contract in the presence of matter and energy.
One problem with this shifting space-time is that as it stretches and shrinks, the density of the energy inside it changes. As a consequence, the classical energy conservation law that previously described all of physics didn’t fit this framework. David Hilbert, one of the most prominent mathematicians at the time, quickly identified this issue and set out with his colleague Felix Klein to try to resolve this apparent failure of relativity. After they were stumped, Hilbert passed the problem on to his assistant, the 33-year-old Emmy Noether.
Noether was an assistant in name only. She was already a formidable mathematician when, in early 1915, Hilbert and Klein invited her to join them at the University of Göttingen. But other faculty members objected to hiring a woman, and Noether was blocked from joining the faculty. Regardless, she would spend the next three years prodding the fault line separating physics and mathematics, eventually setting off an earthquake that would shake the foundations of fundamental physics.
In 1918, Noether published the results of her investigations in two landmark theorems. One made sense of conservation laws in small regions of space, a mathematical feat that would later prove important for understanding the symmetries of quantum field theory. The other, now just known as Noether’s theorem, says that behind every conservation law lies a deeper symmetry.
In mathematical terms, a symmetry is something you can do to a system that leaves it unchanged. Consider the act of rotation. If you start with an equilateral triangle, you’ll find that you can rotate it by multiples of 120 degrees without changing how it looks. If you start with a circle, you can rotate it by any angle. These actions without consequences reveal the underlying symmetries of these shapes.
But symmetries go beyond shape. Imagine you do an experiment, then you move 10 meters to the left and do it again. The results of the experiment don’t change, because the laws of physics don’t change from place to place. This is called translation symmetry.
Now wait a few days and repeat your experiment again. The results don’t change, because the laws of physics don’t change as time passes. This is called time-translation symmetry.
Noether started with symmetries like these and explored their mathematical consequences. She worked with established physics using a common mathematical description of a physical system, called a Lagrangian.
This is where Noether’s insight went beyond the symbols on the page. On paper, symmetries seem to have no impact on the physics of the system, since symmetries don’t affect the Lagrangian. But Noether realized that symmetries must be mathematically important, since they constrain how a system can behave. She worked through what this constraint should be, and out of the mathematics of the Lagrangian popped a quantity that can’t change. That quantity corresponds to the physical property that’s conserved. The impact of symmetry had been hiding beneath the equations all along, just out of view.
In the case of translation symmetry, the system’s total momentum should never change. For time-translation symmetry, a system’s total energy is conserved. Noether discovered that conservation laws aren’t fundamental axioms of the universe. Instead, they emerge from deeper symmetries.
The conceptual consequences are hard to overstate. Physicists of the early 20th century were shocked to realize that a system that breaks time-translation symmetry can break energy conservation along with it. We now know that our own universe does this. The cosmos is expanding at an accelerating rate, stretching out the leftover light from the early universe. The process reduces the light’s energy as time passes.
“Before Noether’s theorem, the principle of conservation of energy was shrouded in mystery,” the physicist and mathematician Feza Gürsey wrote in 1983. “… Noether’s simple and profound mathematical formulation did much to demystify physics.”
Noether’s theorem has shaped the quantum world too. In the 1970s, it played a big role in the construction of the Standard Model of particle physics. The symmetries of quantum fields dictate laws that restrict how fundamental particles behave. For instance, a symmetry in the electromagnetic field forces particles to conserve their charge.
The power of Noether’s theorem has inspired physicists to look toward symmetry to discover new physics. Over a century later, Noether’s insights continue to influence the way physicists think.
“There’s a lot we have left to learn by thinking hard about Noether’s theorem,” the mathematical physicist John Baez said. “It has layers and layers of depth to it.”



