Mathematicians Discover New Way for Spheres to ‘Kiss’

How many spheres can you squeeze around a central sphere?
Michele Sclafani for Quanta Magazine
Introduction
In May of 1694, in a lecture hall at the University of Cambridge, Isaac Newton and the astronomer David Gregory started to contemplate the nature of the stars, only to end up with a math puzzle that would persist for centuries.
The details of their conversation were poorly recorded and are possibly apocryphal — it had something to do with how stars of varying sizes would orbit a central sun. What’s remembered today is the more general question it inspired: Given a central sphere, how many identical spheres can be arranged so that they touch it without overlapping?
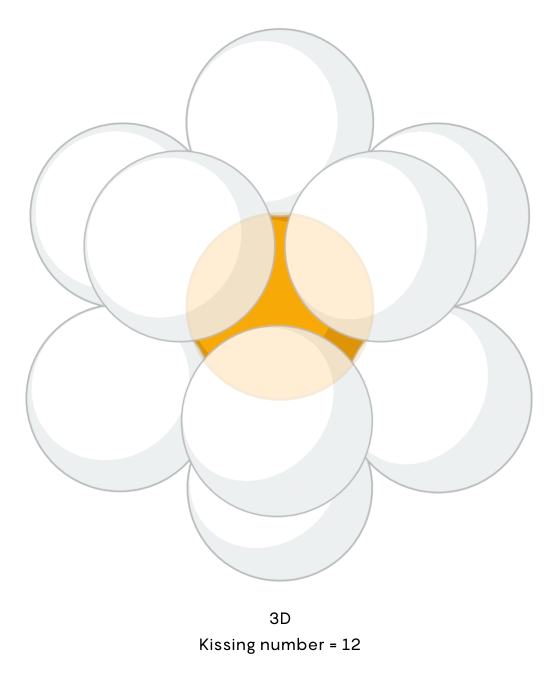
In three dimensions, it’s trivial to position 12 spheres around a central one so that each touches it at a single point. But this arrangement leaves gaps between the spheres. Could you squeeze a 13th into that leftover space? Gregory thought you could. Newton didn’t.
The “kissing” problem, as it came to be called — a reference to when billiard balls strike, or kiss — has proved relevant for analyzing atomic structures, constructing error-correcting codes, and more.
It’s also shaped up to be quite the mathematical challenge. It took mathematicians until 1952 to prove Newton right: In our familiar three dimensions, the maximum “kissing number” is 12.
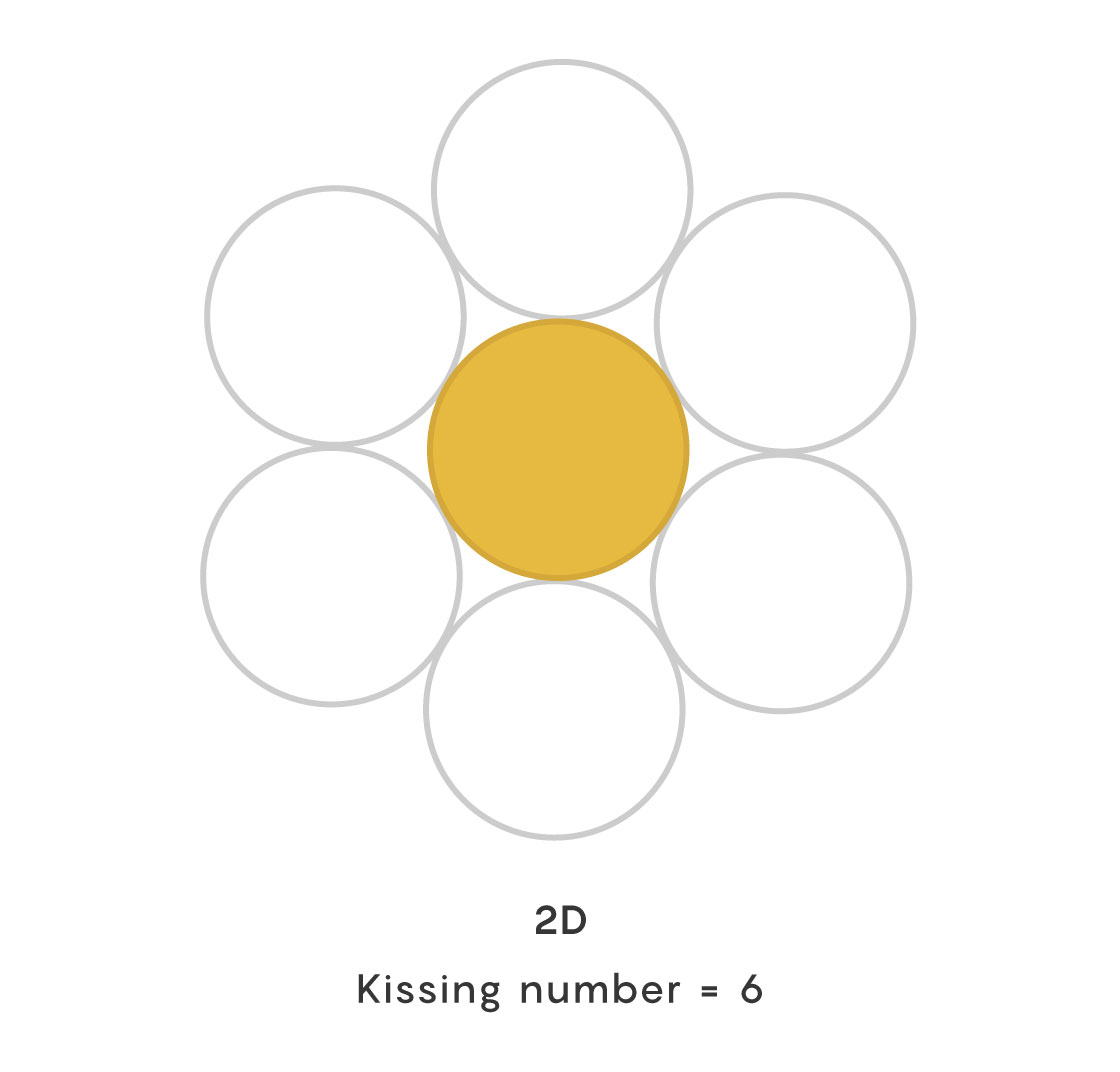
But the kissing problem can be asked about spheres of any dimension. In two dimensions, the answer is clearly six: Put a penny on a table, and you’ll find that when you arrange another six pennies around it, they fit snugly into a daisylike pattern.
In higher dimensions, the problem gets harder.
It has been solved in dimension four, as well as in dimensions 8 and 24, where mathematicians have been able to optimally pack spheres into gorgeously symmetrical lattice structures. But in all other dimensions, where more space appears between the spheres, the problem remains open. Mathematicians have instead come up with estimates of the kissing number, calculating upper and lower bounds that can often be quite far apart. In these cases, the question is no longer about whether you can add a single extra sphere, but about whether you can add hundreds, thousands or even millions.
To improve these estimates, mathematicians usually follow the same intuition that gave them solutions in dimensions like 8 and 24: They look for ways to arrange spheres as symmetrically as possible. But there’s still a possibility that the best arrangements might look a lot weirder. “There may be structures without any symmetry at all,” said Gabriele Nebe of RWTH Aachen University in Germany. “And no good way to find them.”
Then, in the spring of 2022, an undergraduate math major at the Massachusetts Institute of Technology named Anqi Li decided to go looking for those weirder structures. While working on a class project, she came up with a deceptively simple idea that has now allowed her and her professor, Henry Cohn, to improve estimates of the kissing number in a particularly challenging cluster of dimensions: 17 through 21. The work marks the first progress on the problem in those dimensions since the 1960s — and showcases the benefits of injecting more disorder into potential solutions.
“Usually, you work with a very strong symmetric lattice,” said Oleg Musin of the University of Texas, Rio Grande Valley, who proved the optimal kissing number in dimension four in 2003. “What they propose is something different.”
In fact, their proof is the latest in a spate of recent sphere-packing results that were only possible because mathematicians deviated from conventional approaches. “Things stagnated with the kissing problem, but it wasn’t because we were converging on the truth,” Cohn said. “We were just stuck.” To get unstuck, it turned out, they had to break a few unspoken rules.
From Codes to Kisses
Since the mid-20th century, mathematicians have relied on the mathematics of information theory and error correction to make headway on problems related to arranging spheres.
An error-correcting code allows you to send a message that is understandable to the recipient even if parts of it get distorted or corrupted during transmission. The code essentially consists of a set of “code words” — a dictionary of possible messages — that the recipient can use as a key to recover the original message. These code words need to be chosen carefully: They have to be sufficiently distinct for the recipient to know which code word to use when correcting errors.

Anqi Li started working on the kissing problem while she was an undergraduate at MIT. Her research led to exciting advances on several cases of it.
Thea Rossman
Mathematicians often visualize this problem in terms of spheres. You can think of each code word as a high-dimensional point at the center of a sphere. If an error-filled message (when represented as a high-dimensional point) lives inside a given sphere, you know that the code word at the sphere’s center was the intended message. You don’t want these spheres to overlap — otherwise, a received message might be interpreted in more than one way. But the spheres shouldn’t be too far apart, either. Packing the spheres tightly means you can communicate more efficiently.
Better codes have led to better sphere packings, and vice versa. In 1967, for instance, the mathematician John Leech used an incredibly efficient code — famous for its later use by NASA to communicate with its Voyager probes — to construct a lattice of points that now bears his name. Fifty years later, Cohn and several other mathematicians proved that you can use this lattice to pack spheres as densely as possible into 24-dimensional space. The lattice also gives the best kissing arrangement: Each sphere touches 196,560 neighbors. “The Leech lattice is a miracle of mathematics, the way things fit together,” Cohn said.
The lattice also gave mathematicians their best estimates of kissing numbers in dimensions 17 through 23. They simply took slices of the lattice to get lower-dimensional ones, much as you can slice a 3D sphere to get a 2D circle.
But this also meant that the Leech lattice “cast a huge shadow” on the kissing problem in those dimensions, Cohn said. No matter how mathematicians tried, they couldn’t find a structure that gave them better estimates — even though they suspected that taking slices of the Leech lattice wasn’t the right path to a solution.
Going Rogue
Li didn’t initially go looking for a new path when she started working on her project in 2022. At first, Cohn suggested that she focus on the kissing problem in dimensions higher than 24. In those dimensions, the current best estimates of kissing numbers are much rougher. Improving them often comes down to making computational advances rather than finding a creative new approach. Cohn knew of other students who had already made progress in such higher-dimensional cases using computer-based methods. He figured Li could, too.
But she found the work frustrating. “I had this awful feeling that my hands were tied,” she said. “It was impossible to picture.” So instead, she went a little rogue.
She set her sights on dimensions 17 through 23. “I told her she could still get an A if she explored possible improvements and nothing worked out,” Cohn recalled. Had she been one of his graduate students, he would have tried harder to convince her to work on something else. “If they work on something hopeless, it’ll be bad for their career,” he said.
But the result of her efforts, he added, “turned out to be far more exciting.”
She started by looking at dimension 16. There, the best kissing arrangement came from the “Barnes-Wall lattice,” which had been discovered in the 1950s using an elegant error-correcting code. (It also turned out to be a slice of the Leech lattice, which wouldn’t be discovered for another decade.)
The code consists of just two different types of points, which each satisfy a particular pattern of coordinates.
The way these points are defined leads to a quirk: In the Barnes-Wall lattice (and all higher-dimensional slices of the Leech lattice), the most common type of point, or sphere center, always has an even number of minus signs in its coordinates. This helps ensure that there’s enough distance between the points, and results in a symmetric structure that is particularly easy to work with.
But, Li thought, what if she used an odd number of signs in those points instead? If she was careful, that wouldn’t necessarily lead to overlapping spheres. To her knowledge, no one had bothered trying it before. “I don’t think either of us really thought that it mattered,” Cohn said. But Li suspected that there was a chance that, by changing some of the points in the lattice in this way, she might be able to distort it just enough to accommodate more spheres.
When she built her “odd” version of the Barnes-Wall lattice in dimension 16, it yielded no space for extra spheres, though it didn’t make anything worse either. But when she glued copies of it together into layers to make a 17-dimensional structure, there were clearly gaps where new points could be added — holes where, when she calculated the distance to existing spheres in the structure, it was clear that new spheres could fit. At first, she couldn’t believe it. She felt uneasy, not elated. “I remember telling my friends, I’m sure I did some basic arithmetic wrong,” she said.
Cohn indulged her skepticism at first — it’s easy to make a little mistake in these kinds of calculations, especially when wishful thinking might be involved. So they checked her new arrangement of points on a computer. It worked: All the spheres fit correctly.
That summer, Li went to work with Cohn as an intern at Microsoft Research, where the pair carefully refined the error-correcting codes they were using so that they could continue adding compatible spheres to Li’s “odd” 17-dimensional structure. In the end, they were able to add 384 new spheres to the Leech-based estimate from 1967, bringing the lower bound of the kissing number to 5,730.
They then applied similar techniques to improve the kissing number in dimensions 18 through 21. But in dimensions 22 and 23, their strategy failed. It seemed they’d exhausted their sign-flipping approach.
The pair’s new configurations likely aren’t optimal. In dimension 17, for instance, the estimated upper bound is 10,978; while that’s considered a gross overestimate of the real solution, it suggests that there is still significant room to improve the lower bound.
But mathematicians are more interested in how Cohn and Li achieved their gains. Their new structures look very different from the highly symmetric ones inspired by the Leech lattice. The code-based methods they used to add spheres gave them more irregular configurations — something entirely new.
A New Way Forward
It’s not clear why changing the signs creates enough space for more spheres. It just does. “I’m still unnerved by it now,” Cohn said. But the work demonstrates how a “seemingly insignificant change opens up or closes off possibility,” he added. It reveals, in that sense, how little mathematicians actually know about the kissing problem.
When building new error-correcting codes and sphere packings, mathematicians generally rely on symmetry. That’s what Leech did. This makes the construction process easier, more intuitive. But it can also close off possibilities, making it hard to see beyond a beautiful solution to other structures — ones that might have more disorder or involve less intuitive forms of symmetry. “Maybe we’re not coming near the truth because it just doesn’t have a humanly accessible description,” Cohn said.
Several recent results support the promise of these less accessible possibilities. In the past couple of years, mathematicians have come up with clever new constructions in dimensions 5, 10 and 11 by bending or breaking the usual symmetry rules.
Cohn was particularly astonished by the work of Ferenc Szöllősi, a Hungarian mathematician who intentionally started with a suboptimal arrangement of spheres in dimension four and built on it to match the best existing estimate in dimension five. For decades, there were two structures that generated that estimate; most mathematicians thought there couldn’t be any others. Suddenly here was Szöllősi with a third. (He later found out that another pair of researchers had also discovered the configuration, but they had not recognized its significance.) “It proved you could be taken by surprise,” said Cohn, who was then inspired to work with another one of his students to find a fourth.
Every unusual structure they discover gives them “little hints and clues to what the truth might be,” he added. “The kissing problem is still full of mysteries.”
Correction: January 16, 2025
Ferenc Szöllősi’s result was also independently discovered by another pair of mathematicians. The text has been updated to include mention of that other work.